На ориентированной плоскости

Угол от одного вектора до другого

Теорема 1. Введем на плоскости ортонормированный базис: 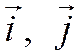(этим самым плоскость ориентирована). Пусть 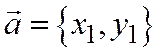и 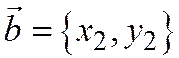- ненулевые векторы, координаты которых даны относительно базиса .

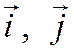Тогда имеют место формулы:

1) ;

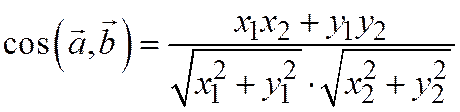2) ;

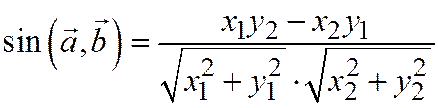3) .

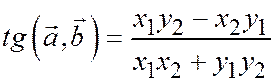Причем формула 3 имеет место тогда и только тогда, когда векторы 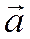и 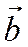не взаимно перпендикулярны.

Доказательство. На основании теоремы Шаля имеем:

4) 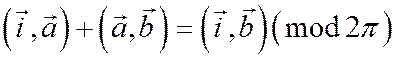, или

5) .

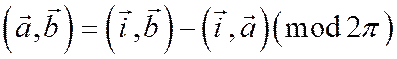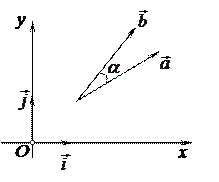Введем декартовую прямоугольную систему координат, выбирая произвольно начало координат О, ось Ох направим по вектору 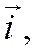ось Оу по вектору 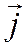и примем эти векторы 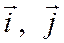за масштабные векторы, соответственно для осей Ох и Оу (см.рис).

На основании определения тригонометрических функций имеем:

;

. .

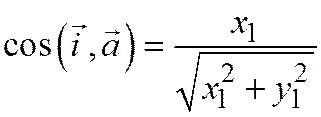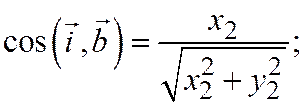
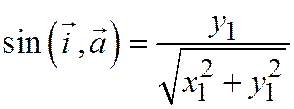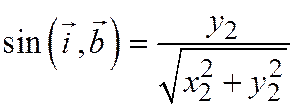Отсюда, и из отношения 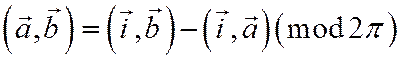находим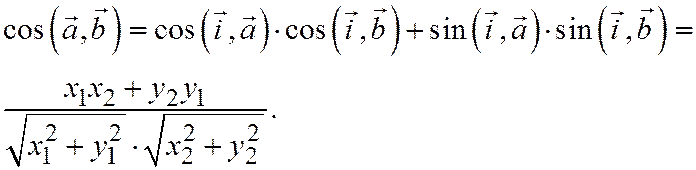

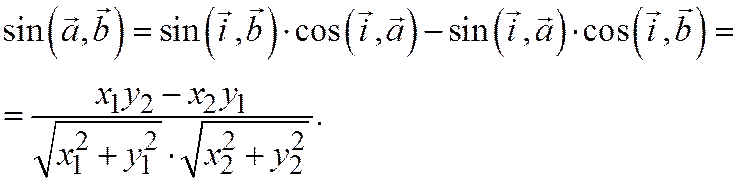Из полученных выражений для 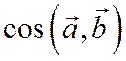и 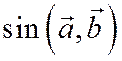в случае 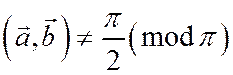получим формулу для тангенса:

.

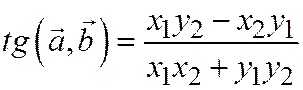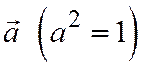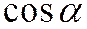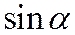Замечание. Если на плоскости введен ортонормированный базис, то координаты единичного вектора равны соответственно и , где 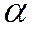- угол от вектора 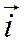до вектора 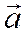, т.е. 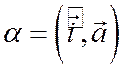. Это следует из формулы 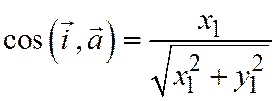и 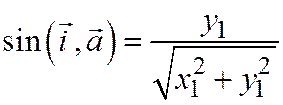. А так как вектор 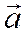единичный, то .

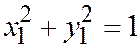Теорема 2. Если на плоскости введен ортонормированный базис 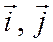(этим плоскость ориентирована), и относительно этого базиса задан ненулевой вектор 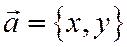, а вектор 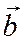получен из вектора 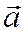поворотом на угол 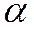, то

.

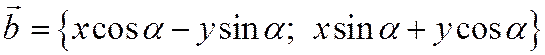Доказательство. Из соотношений 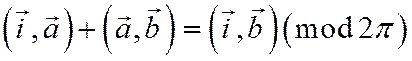, находим:

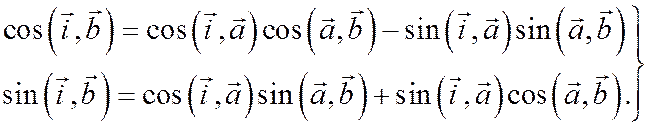(9)

По определению тригонометрических функций

; ;

; ,

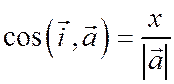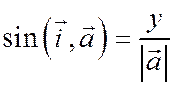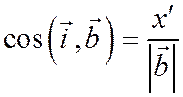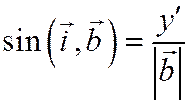где 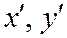- координаты вектора .

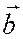Из этих формул и соотношений в фигурных скобках (9) следует, что

.

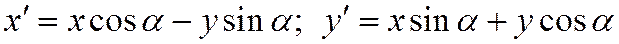Следствие. Будем обозначать через 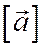вектор, полученный из ненулевого вектора 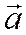лежащего в ориентированной плоскости, поворотом на угол 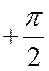. Тогда, если в ортонормированном базисе 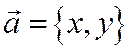то 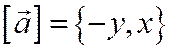. В самом деле, это сразу следует из формул 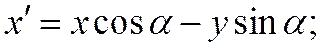, , 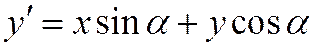если положить в них 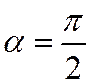(см. рис).

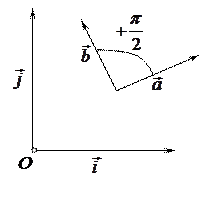
Дата добавления: 2014-01-07