
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Z – преобразование
|
|
|
|
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА.
ЛЕКЦИЯ 16
План лекции
1. Понятие о D и Z - преобразованиях.
2. Область применения D и Z - преобразований.
3. Обратные D и Z - преобразования.
В прикладных исследованиях, связанных с использованием решетчатых функций, широко применяется дискретное преобразование Лапласа (Д – преобразование) и Z – преобразование. По аналогии с обычным преобразованием Лапласа дискретное задается в виде
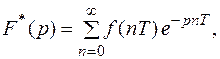 где (1)
где (1)

Символически Д – преобразование записывается в виде

Для смещенных решетчатых функций
 (2)
(2)
где  - смещение.
- смещение.
Z – преобразование получается из Д – преобразования подстановкой  и задается соотношением
и задается соотношением
 (3)
(3)
Для смещенной функции

Функция  называется оригиналом, если
называется оригиналом, если
1) 
2) существует показатель роста, т. е. найдутся такие 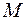 и
и 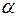 , что
, что
 (4)
(4)
Наименьшее из чисел 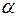 (или предел, к которому стремится наименьшее число), для которого справедливо неравенство (4), называется абсциссой абсолютной сходимости и обозначается
(или предел, к которому стремится наименьшее число), для которого справедливо неравенство (4), называется абсциссой абсолютной сходимости и обозначается 
Теорема.
Если функция  является оригиналом, то изображение
является оригиналом, то изображение 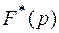 определено в области Re p >
определено в области Re p >  и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Покажем, что при Re p >  ряд (1) абсолютно сходится. Имеем
ряд (1) абсолютно сходится. Имеем



т. к. указанная сумма представляет собой сумму членов убывающей геометрической прогрессии с показателем 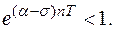 Известно, что такая прогрессия сходится. Величину
Известно, что такая прогрессия сходится. Величину 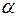 можно взять сколь угодно близкой величине
можно взять сколь угодно близкой величине  , т. е. первая часть теоремы доказана.
, т. е. первая часть теоремы доказана.
Вторую часть теоремы примем без доказательств.
Изображение 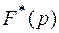 является периодической функцией с мнимым периодом
является периодической функцией с мнимым периодом 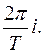


При изучении изображения 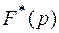 нет смысла рассматривать его на всей комплексной плоскости, достаточно ограничиться изучением в любой полосе шириной
нет смысла рассматривать его на всей комплексной плоскости, достаточно ограничиться изучением в любой полосе шириной  Обычно на комплексной плоскости используется полоса,
Обычно на комплексной плоскости используется полоса,  которая называется основной. Т. о. Можно считать, что изображения
которая называется основной. Т. о. Можно считать, что изображения 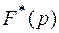 определено в полу полосе
определено в полу полосе
|
|
|
 и является в этой полу полосе аналитической функцией.
и является в этой полу полосе аналитической функцией.
 |
 |
Найдем область определения и аналитичности функции F(z), положив  . Покажем, что полу полоса
. Покажем, что полу полоса  плоскости p преобразованием
плоскости p преобразованием  переводится в область на плоскости z:
переводится в область на плоскости z:  .
.
Действительно, отрезок  , ограничивающий полу полосу на плоскости p, переводится на плоскости z в окрестность:
, ограничивающий полу полосу на плоскости p, переводится на плоскости z в окрестность:  .
.
Обозначим через  линию, в которую преобразование
линию, в которую преобразование  переводит отрезок
переводит отрезок  . Тогда
. Тогда



 т. о.
т. о.
 окрестность
окрестность  .
.
Т. о. Z – преобразование F(z) определено в области  и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Обратное Д – преобразование позволяет по изображению 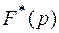 восстановить решетчатую функцию
восстановить решетчатую функцию 
 |
 (5)
(5)
 |
Докажем справедливость равенства.


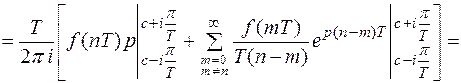



Получим из равенства (5) формулу для обратного Z – преобразования. Воспользуемся подстановкой  . Рассмотренным выше способом легко установить, что отрезок
. Рассмотренным выше способом легко установить, что отрезок 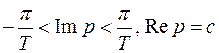 с помощью преобразования
с помощью преобразования  переводится на плоскости Z в окрестность
переводится на плоскости Z в окрестность 
 .
.
Тогда из (5) следует
 (6)
(6)
Равенство (6) задает обратное Z – преобразование, т. е. позволяет по функции F(z) восстановить решетчатую функцию f(nT).
Т. к.  , то все особые точки функции F(z) и, следовательно, функции
, то все особые точки функции F(z) и, следовательно, функции  лежат внутри окрестности
лежат внутри окрестности 
Из (6) следует, что

Вычеты берутся по всем особым точкам.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 589; Нарушение авторских прав?; Мы поможем в написании вашей работы!