Векторные уравнения Пуассона и Лапласа

Из уравнения (4) следует, что векторное поле B можно представить в виде ротора некоторого векторного поля:

B= rot A (6)

Здесь векторное поле A называется векторным магнитным потенциалом.

Подставив (6) в (5), а затем (5) в (3), получим

(7)

(7) является уравнением магнитостатического поля относительно векторного магнитного потенциала.

Для обеспечения единственности решения этого уравнения кроме граничных условий необходимо ввести условие калибровки, накладывающее ограничение на дивергенцию векторного магнитного потенциала. Наиболее простым условием является div A = 0. Преобразуем уравнение (7) с учетом этой калибровки. Для этого левую часть (7) запишем в виде:

или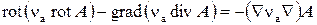

Поскольку div A = 0, из левой части (7) можно вычесть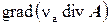, значит (7) преобразуется к виду:

(8)

(8) называется векторным уравнением Штурма-Луивиля. Это уравнение пригодно для расчета магнитостатических полей в однородных и кусочно-однородных средах, причем на поверхностях раздела сред выполняется условие A _{1 t} = A _{2 t}, т.е. тангенциальная составляющая векторного магнитного потенциала непрерывна. В областях, где = соnst, можно вынести за знак дифференциальных операторов, тогда уравнение (8) примет вид:

(9)

В областях, где δ = 0 и B _r = 0, распределение векторного потенциала описывается уравнением:

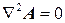(10)

(9) называется уравнением Пуассона, а (10) – векторным уравнением Лапласа.

В декартовой системе координат уравнение (9), а значит и (10) распадается на три независимых скалярных уравнения:

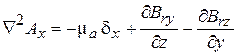
Краевая задача магнитостатики для неоднородных сред

Для расчета магнитостатического поля в неоднородной среде необходима другая модификация уравнения (7) с учетом условия калибровки, Если из левой части (7) вычесть 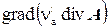, где – удельное магнитное сопротивление среды, занимающей наибольший объем в расчетной области, тогда получим:

(11)

Уравнение (11) позволяет представлять магнитостатическое поле в неоднородной среде непрерывным полем векторного магнитного потенциала. Это даёт возможность применять конечноразностные и конечноэлементные методы без существенных ограничений.

Для обеспечения единственности решения уравнения (11) его необходимо дополнить граничными условиями для искомого потенциала или для тангенциальной составляющей вектора напряженности магнитного поля на поверхности, ограничивающей расчетную область, т.е.

A = поверхностное распределение – на части граничной поверхности Г₁,

H _t = поверхностное распределение – на части граничной поверхности Г₂

Г = Г₁ + Г₂ – замкнутая граничная поверхность.

При анализе и моделировании магнитостатических полей необходимо учитывать, что аналогия уравнений магнитостатического и электростатического поля имеет место только в простейших случаях.

Дата добавления: 2014-01-07