Тема 10: оптимальные линейные фильтры

Как много дел считалось невозможными, пока они не были осуществлены.

Гай Плиний Секунд (философ).

Специалисты в науке подобны старателям. Стоит одному найти крупинку золота, как другие выроют в этом месте котлован. А тема оптимальности, это вообще золотое Эльдорадо, можно копать в любом направлении.

Володя Старцев (Геофизик).

Содержание: 10.1. Модели случайных процессов и шумов. Белый шум. Фильтрация белого шума. 10.2. Критерии построения оптимальных фильтров. Среднее квадратическое отклонение. Амплитудное отношение сигнал/шум. Энергетическое отношение сигнал/шум. 10.3. Фильтр Колмогорова-Винера. Условие оптимальности фильтра. Система линейных уравнений фильтра. Частотная характеристика фильтра. Эффективность фильтра. 10.4. Оптимальные фильтры сжатия сигналов. Частотная характеристика. Условие оптимальности. 10.5. Фильтр прогнозирования. 10.6. Фильтр обнаружения сигналов. Частотная характеристика. Система линейных уравнений. Эффективность фильтра. Согласованный фильтр. Обратный фильтр. 10.7. Энергетический фильтр. Критерий оптимальности. Расчет векторов операторов фильтров. Литература.

10.1. Модели случайных процессов и шумов /л12/.

Результаты практических измерений, подлежащие обработке, содержат определенный полезный сигнал на фоне различного рода помех (шумов), при этом спектр помех в общем случае недетерминирован и в той или иной мере представлен по всему интервалу главного частотного диапазона. Другими словами, спектр полезного сигнала наложен на спектр шумов. В этих условиях ставится задача реализации так называемых оптимальных фильтров, которые, в зависимости от своего конкретного назначения, позволяют достаточно надежно производить обнаружение сигнала, наилучшим образом выделять сигнал на фоне помех или в максимальной степени подавить помехи без существенного искажения сигнала.

Случайные процессы и шумы описываются функциями автокорреляции и спектрами мощности. Модели случайных процессов (сигналов) с заданными статистическими характеристиками обычно получают фильтрацией белого шума.

Белый шум q(t) можно представлять как случайную по времени (аргументу) последовательность дельта - импульсов d(t_i) со случайными амплитудными значениями a_i:

q(t) = S_i a_id(t-t_i), (10.1.1)

которая удовлетворяет условиям статистической однородности: постоянное среднее число импульсов в единицу времени и статистическая независимость появления каждого импульса от предыдущих. Такой поток импульсов, который называют пуассоновским, является некоррелированным и имеет равномерный спектр мощности:

R_q(t) = c²d(t), W_q(w) = c²,

где с² = Ns_a², N - число импульсов на интервале Т реализации случайного процесса, s_a² -дисперсия амплитуд импульсов.

Фильтрация белого шума. Если на входе фильтра с импульсным откликом h(t) действует белый шум q(t), то сигнал на выходе фильтра:

g(t) = h(t) _* q(t) = h(t) 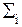_*a_id(t-t_i) =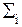a_i h(t-t_i), (10.1.2)

т.е. выходной сигнал будет представлять собой последовательность сигналов импульсной реакции фильтра h(t) с амплитудой a_i, при этом автокорреляционная функция и спектр мощности выходного потока также становятся подобными ФАК и спектру мощности импульсной реакции фильтра и в первом приближении определяются выражениями:

R_g(t)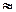N d_a² R_h(t) = c² R_h(t), (10.1.3)

W_g(w) 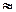N d_a² |H(w)|² = c² |H(w)|². (10.1.4)

Этот результат известен как теорема Кэмпбелла.

10.2. Критерии построения оптимальных фильтров.

В практике обработки геофизических данных используются три основных критерия построения оптимальных фильтров: минимум среднего квадратического отклонения профильтрованного сигнала от его действительного или заданного значения, максимум отношения сигнал/шум и максимум энергетического отношения сигнал/шум на выходе фильтра. При анализе и синтезе фильтров используется аддитивная модель входного сигнала: x(k) = s(k)+q(k), где s(k) - полезная составляющая сигнала, q(k) - составляющая помех. Синтез оптимальных фильтров производится с максимальным использованием известной априорной информации как о сигналах, которые необходимо выделить, так и о шумах и помехах. Как правило, используется информация о природе полезного сигнала и шума, об их спектральном составе, о корреляционных и взаимно корреляционных характеристиках. Наличие определенных особенностей (различий) в характеристиках сигнала и шума позволяет реализовать фильтр вообще и оптимальный фильтр в частности. Если такие особенности отсутствуют, постановка задачи становится некорректной.

В геофизической практике априорные данные о полезных сигналах, как правило, являются достаточно определенными, особенно для активных методов геофизики (сейсмические методы, электроразведка на переменном токе, индукционные методы ядерной геофизики и пр.). Определение характеристик действующих помех представляет собой более сложную проблему, но даже при полной неопределенности можно допустить, что помеха является нормальным стационарным процессом с нулевым средним значением.

Среднее квадратическое отклонение. При наличии помех абсолютно точное выделение полезного сигнала методами линейной фильтрации, как правило, невозможно. Результат фильтрации

y(k) = h(n) _* x(k-n) (10.2.1)

отличается от s(k) на величины e(k) = y(k)-s(k), которые являются абсолютными значениями погрешности воспроизведения полезного сигнала по координатам k. Качество фильтра оценивается средним значением квадрата величины e(k):

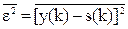. (10.2.2)

Во многих задачах обработки геофизических данных не требуется восстановления исходной формы сигнала s(k), т.к. в процессе его дальнейшей обработки осуществляется преобразование сигнала s(k) в сигнал z(k), форма которого может быть более удобной для извлечения (измерения) каких-либо информационных параметров сигнала (например - амплитудного значения, ширины сигнала на половине максимального значения и т.п.). В этом случае оптимальный фильтр может проектироваться непосредственно на получение выходного сигнала z(k). Качество таких фильтров, получивших название формирующих, оценивается средним значением квадрата величины e(k) получения сигнала заданной формы:

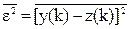. (10.2.2')

Выражения (10.2.2) дают возможность определить значения h(k) фильтра по критерию минимума среднего квадратического отклонения выходного сигнала от его действительной или заданной формы. Еще раз отметим, что данный критерий исходит из вероятностно - статистической модели экспериментальных данных и хорошо себя показал при обработке геофизических данных, но его возможности могут быть ограничены при количественной интерпретации геофизических аномалий.

Амплитудное отношение сигнал/шум. При постановке задачи обнаружения (установления факта наличия) в экспериментальных данных сигнала известной формы для проектирования фильтра используется, как правило, критерий максимума пикового отношения сигнал/шум на выходе фильтра:

r_а = y_экс/s,

где y_экс - экстремальное (максимальное или минимальное) значение амплитуды сигнала, s - средний квадратический уровень амплитудных значений помех (s² - дисперсия помех). Если в полезном сигнале отсутствует четко выраженный экстремум, а сам сигнал достаточно протяженный по аргументу (что обычно имеет место в геофизической практике), то в качестве критерия используется отношение средних квадратов амплитуд сигнала и шума:

, (10.2.3)

где y² - средний квадрат амплитуды сигнала в пределах его формы.

Энергетическое отношение сигнал/шум. При узко конкретной задаче обнаружения сигнала степень искажения самого сигнала может не ограничиваться. Если кроме обнаружения сигнала, как основной цели обработки данных, ставится и задача оценки его формы, то в этом случае для проектирования фильтра обычно используется критерий максимума энергетического отношения сигнал/шум:

r = Е_sy/E_qh, (10.2.4)

где Е_sу и E_qh - энергия соответственно сигнала и шума на выходе фильтра.

10.3. Фильтр Колмогорова-Винера.

Условие оптимальности фильтра. Подставим (10.2.1) в выражение (10.2.2') и получим среднее квадратическое отклонение e² формы выходного сигнала y(k) = h(n)_*x(k-n) от оптимальной формы z(k) по всем точкам массива данных (в частном случае z(k) = s(k)):

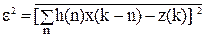. (10.3.1)

Минимум функции (10.3.1) определяет значения коэффициентов h(n) оптимального фильтра. Для нахождения их значений продифференцируем выражение (10.3.1) по коэффициентам фильтра и приравняем полученные уравнения нулю. В итоге получаем:

,

где 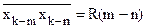- корреляционная функция входного сигнала, 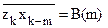- взаимная корреляционная функция сигналов z(k) и x(k). Отсюда:

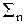h_nR(m-n) = B(m), n = m = 0,1,2,..., M. (10.3.2)

В краткой форме записи:

h(n)_*R(m-n) = B(m). (10.3.3)

Другими словами, свертка функции отклика фильтра с функцией автокорреляции входного сигнала должна быть равна функции взаимной корреляции входного и выходного сигналов.

Система линейных уравнений фильтра. Выражение (10.3.2) может быть записано в виде системы линейных уравнений - однострочных равенств левой и правой части для фиксированных значений m. С учетом четности функции автокорреляции:

m=0: h_oR(0)+ h₁R(1)+ h₂R(2)+ h₃R(3)+...+ h_MR(M) = B(0),

m=1: h_oR(1)+ h₁R(0)+ h₂R(1)+ h₃R(2)+...+ h_MR(M-1) = B(1),

m=2: h_oR(2)+ h₁R(1)+ h₂R(0)+ h₃R(1)+...+ h_MR(M-2) = B(2),

..............................................................................................................

m=M: h_oR(M)+ h₁R(M-1)+ h₂R(M-2)+.... + h_MR(0) = B(M).

Решение данной системы уравнений относительно значений h_i дает искомый оператор фильтра.

Отметим, что R(i) = R_s(i)+R_q(i), где R_s - функция автокорреляции сигнала, R_q - функция автокорреляции шума, а B(i) = B_zs(i)+B_zq(i), где B_zs - функция взаимной корреляции сигналов z(k) и s(k), B_zq - функция взаимной корреляции сигнала z(k) и помех q(k). Подставляя данные выражения в (10.3.3), получаем:

h(n)_*[R_s(m-n)+R_q(m-n)] = B_zs(m)+B_zq(m). (10.3.4)

Частотная характеристика фильтра находится преобразованием Фурье левой и правой части уравнения (10.3.4):

H(w)[W_s(w)+W_q(w)] = W_zs(w)+W_zq(w),

H(w) = [W_zs(w)+W_zq(w)] / [W_s(w)+W_q(w)], (10.3.5)

где W_s(w) ó R_s(m) и W_q(w) ó R_q(m) - энергетические спектры сигнала и помех, W_zs(w) ó B_zs(m) - взаимный энергетический спектр входного и выходного сигналов, W_zq(w) ó B_zq(m) - взаимный энергетический спектр выходного сигнала и помех.

В геофизической практике обычно имеет место статистическая независимость полезного сигнала, а, следовательно, и сигнала z(k), от шумов, при этом B_zq = 0 и фильтр называют оптимальным по сглаживанию шумов при заданной форме выходного сигнала:

H(w) = W_zs(w) / [W_s(w)+W_q(w)], (10.3.6)

Если при этом заданная форма сигнала z(k) совпадает с формой полезного сигнала s(k), то B(m) = B_ss = R_s и фильтр называют фильтром воспроизведения полезного сигнала:

H(w) = W_s(w) / [W_s(w)+W_q(w)], (10.3.7)

Эффективность фильтра. Из выражений (10.3.5-7) наглядно видно, что с позиции минимального искажения полезного сигнала при максимальном подавлении шумов фильтр Колмогорова-Винера эффективен в тем большей степени, чем больше отношение сигнал/шум на входе фильтра. В пределе, при W_q(w)<<W_s(w) имеем H(w)Þ 1 и фильтр воспроизводит входной сигнал без искажений. Отметим также, что помеха, коррелированная с полезным сигналом, как это следует из (10.3.5), используется фильтром для повышения точности воспроизведения сигнала. С другой стороны, при W_q(w)>>W_s(w) имеем H(w) Þ 0 и сигнал будет сильно искажен, но никакой другой фильтр лучшего результата обеспечить не сможет.

Если сигнал, подлежащий воспроизведению, не относится к числу случайных и представляет собой какую-либо детерминированную функцию, то W_s(w) = |S(w)|².

10.4. Оптимальные фильтры сжатия сигналов.

Частотная характеристика идеального фильтра, осуществляющего сжатие сигнала s(k) к дельта-функции, определяется выражением:

H(w) = 1/S(w) = S*(w) / |S(w)|², (10.4.1)

где S*(w) - комплексно сопряженный спектр полезного сигнала. На выходе такого фильтра имеем:

Y(w) = H(w)X(w) → 1, при X(w) → S(w).

Реализация фильтра возможна только при условии S(w) > 0 на всех частотах в главном частотном диапазоне. В противном случае, при S(w_i) → 0, H(w_i) → ∞ и фильтр становится неустойчивым. Для исключения возможности такого явления в фильтр (10.4.1) вводится стабилизатор a:

H(w) = S*(w) / [|S(w)|²+a], (10.4.2)

где |S(w)|²+a > 0 во всем частотном диапазоне.

Условие оптимальности. Фильтр сжатия сигнала может быть получен с использованием уравнения (10.3.3).

Положим, что z(k)=d(k) при статистической независимости сигнала и шума. Отсюда:

B_sz(m) = d(m) _* s(k+m) = s(-m).

h(n) _* (R_s(m-n)+R_q(m-n)) = s(-m).

H(w) = S*(w) / (|S(w)|²+W_q(w)). (10.4.3)

Сравнение выражений (10.4.2) и (10.4.3) показывает, что оптимальной величиной стабилизатора a является значение спектральной плотности помех. При некоррелированной помехе с дисперсией s² система уравнений для определения значений коэффициентов h(n):

h_o(R(0)+s²)+ h₁R(1)+ h₂R(2)+ h₃R(3)+...+ h_MR(M) = s(0),

h_oR(1) + h₁R(0)+ h₂R(1)+ h₃R(2)+...+ h_MR(M-1) = 0,

h_oR(2) + h₁R(1)+ h₂R(0)+ h₃R(1)+...+ h_MR(M-2) = 0,

Дата добавления: 2014-01-07