Анализ поведения множества точек

Заранее определить, принадлежит ли точка (a,b) множеству Мандельброта нельзя.

На каждом шаге, кроме очередных значений Х_i+1 и У_i+1, вычисляют расстояние точки с координатами (X,Y) от начала координат

. (3)

На комплексной плоскости различаются три типа точек.

1. Если орбита точки никогда не "убегает" из области определенного диаметра R, расположенной в начале координат комплексной плоскости, то эта точка - элемент множества Мандельброта. Точки, удовлетворяющие этому критерию, обычно закрашиваются черным цветом. Это равновесные (статические) точки. Область, ограниченная критическим расстоянием R, представляет область притяжения или аттрактор. Аттракторами называют точки или замкнутые линии, притягивающие к себе возможные траектории поведения системы.

2. Для всех прочих значений a и b величина r_i может переходить запретный рубеж за разное количество шагов.

Существует теорема: если точка, удалится от начала координат на две и более единиц, то она уйдет в бесконечность и окажется за пределами множества Мандельброта.

Такие точки не принадлежат множеству Мандельброта. Они свободно путешествуют по плоскости, уходя в бесконечность. Такие точки окрашивают в белый цвет. Бесконечность является еще одной областью притяжения или аттрактором.

Таким образом, фазовое пространство системы разбивается на области притяжения - аттракторы. Аттракторы – это центры, ведущие борьбу за доминирование на плоскости. Состояние, в котором окажется динамическая система после некоторого числа итераций, зависит от ее начального состояния.

3. Между аттракторами возникает граница, представляющая витиеватый узор. Любая начальная точка Х₀ либо в течение процесса приходит к тому или иному центру, либо лежит на границе, где она не может принять определенное решение. С изменением параметра (а, b) изменяются и области, принадлежащие аттракторам, а вместе сними и границы.

Таким образом, множество Мандельброта - это множество точек (a, b), которые устремляются к разным аттракторам. Сначала возникает темный плоский широкий круг с рваными краями. Затем он начинает делиться на части, все более расчленяется и одновременно пробивается к поверхности. Происходит борьба, в результате которой рождаются невероятные образования. Эти контуры настолько сложны, что мельчайшие их детали теряются в бесконечности.

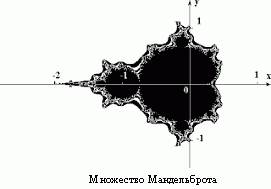
Так получается изображение множества Мандельброта и его окружение с "нестабильными" областями фрактала - областями, для которых малые изменения формулы ведут к большой разнице в орбитальном поведении. Меняя формулу для подсчета орбит, получим другие, такие же экзотические фракталы.

Бесконечное количество деталей при любой степени увеличения есть основная отличительная черта фрактальных кривых и поверхностей.

По утверждениям математиков, множество Мандельброта связано. Связность множества Мандельброта означает, что ни одна из его частей не отделена от основного тела, но все они связаны вместе исключительно тонкими линиями. Однако маршрут по этому множеству не будет похож ни на одну земную дорогу. Если последовательно увеличивать практически любую из ветвей, окружающих множество Мандельброта, то видны будут лишь цепочки крошечных черных островков, которые кажутся не связанными друг с другом. Конечно, мы найдем цепочки более мелких островков между крупными островами, однако непрерывная дорога встречается редко или вообще не обнаруживается ни при каком увеличении. Мельчайшая деталь границы, показанная в трех разных вариантах раскраски, дает представление об изумительной системе мостов, необходимой для обеспечения связности.

Благодаря своему бесконечно сложному строению "кружева" границы множества Мандельброта имеют фрактальную размерность, равную двум, при топологической размерности - 1.

Дата добавления: 2014-01-07