Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Модель линейно-деформируемого слоя ограниченной толщины

Модель упругого полупространства

Эта модель была предложена и развита в трудах Г.Э.Проктора, Н.П.Пузыревского, Н.М.Герсеванова, М.И.Горбунова-Посадова, Б.Н.Жемоч-кина, И.А.Символиди и др. В отличие от предыдущей модели в этом случае поверхность грунта оседает как в пределах площади загрузки, так и за ее пределами. Грунт рассматривается как линейно-деформируемая среда. Модуль упругости заменяется понятием "модуль общей деформации".

Развитие теории расчета конструкций на слое ограниченной толщины принадлежит С.С.Давыдову, К.Е.Егорову, О.Я.Шехтер и др. В основе модели лежит предположение о том, что с фундаментом взаимодействует определенная толщина грунтового массива, ниже которой находится недеформируемая область, жесткость которой может быть принята бесконечно большой. В этом случае есть возможность полнее учесть деформационные параметры основания.

Возведение тяжелых сооружений, передающих на основание значительные силовые воздействия, строительство на слабых, сильносжимаемых грунтах, в сложных инженерно-геологических условиях заставило перейти к более сложным моделям основания, учитывающим нелинейную зависимость между напряжениями и деформациями. В этом направлении следует отметить труды Г.М.Ломизе, Б.И.Дидуха, Ю.К.Зарецкого, А.Л.Крыжановского, В.А.Иоселевича, А.К.Бугрова, З.Г.Тер-Мартиросяна, В.И.Соломина, Л.А.Бартоломея и др.

Практика расчетов показывает, что модель местных упругих деформаций дает хорошую сходимость с действительными осадками при возведении фундаментов на сильносжимаемых грунтах при модуле общей деформации менее 50 МПа, модель упругого полупространства применима при наличии в основании плотных грунтов и не слишком больших площадей фундаментов. Для сооружений с площадью опирания в десятки квадратных метров хорошую сходимость с действительными осадками дает модель упругого слоя ограниченной мощности.

Пространственная задача. Теория распределения в грунтовом пространстве напряжений, возникающих от действия сосредоточенной силы, представляют собой исходную теорию для расчета грунтовых оснований, нагруженных более сложными реальными нагрузками, распределенными на площади основания по разным закономерностям. Поэтому в начале мы рассматриваем приложение сосредоточенной силы к поверхности линейно-деформируемого однородного изотропного полупространства. Величина напряжений в любой точке полупространства была найдена французским ученым Буссинеском в 1885 г.

На схеме (рис.3.7) выделим точку М с полярными координатами R и b. Определим напряжения, действующие в точке М на площадку, перпендикулярную радиусу R. Для определения радиального напряжения s _R проделаем следующее: рассмотрим перемещение точки М в направлении радиуса R. Чем дальше от точки приложения внешней силы Р находится рассматриваемая точка М ₁, тем меньше будет ее перемещение. При одной и той же величине R перемещения точек, соответствующих различным углам b, будут различны; наибольшее перемещение произойдет по оси z (при b=0), наименьшее - по оси y (при b = 90^о).

Рис.3.7. Схема деформации точки М в нагруженном полупространстве

Исходя из вышеизложенного, можно принять, что перемещение точки М в направлении радиуса R будет

, (3.6)

где A – неизвестный нам коэффициент пропорциональности.

Аналогично предыдущему, перемещение точки М ₁, расположенной от точки М на расстоянии dR, будет

. (3.7)

Относительная деформация отрезка dR выразится в виде

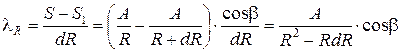. (3.8)

Пренебрежем величиной RdR, как ничтожно малой по сравнению с R ², и тогда получим

.

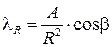Поскольку напряжения пропорциональны деформациям, мы можем написать выражение для радиального напряжения s _R в точке М:

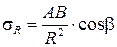, (3.9)

где B – неизвестный нам коэффициент пропорциональности.

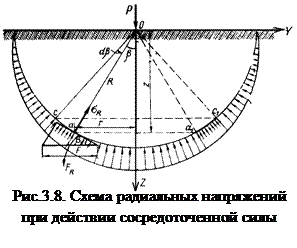Для определения коэффициентов А и В проведем полушаровое сечение радиусом R с центром в точке приложения внешней силы Р (рис.3.8). По поверхности полушара будут приложены радиальные напряжения s _R, переменность величины которых определяется только величиной угла b. Интенсивность напряжений s _R одинакова для каждого элементарного шарового пояса, отвечающего центральному углу d b.

Из условий равновесия сумма проекций всех сил на вертикальную ось должна быть равна нулю

, (3.10)

где dF – поверхность элементарного шарового пояса,

dF =2p(R sin b)(Rdb). (3.11)

Подставляем значения dF в уравнение равновесия и решаем интеграл:

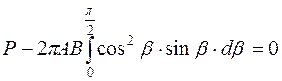. (3.12)

,

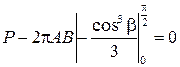, откуда .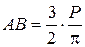

Подставляя полученные значения коэффициентов АВ в формулу (3.9), получим

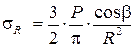. (3.13)

Пользуясь полученным выражением, можно найти напряжение в любой точке линейно-деформируемого массива, нагруженного с поверхности сосредоточенной силой Р.

В практике пользование радиальными напряжениями неудобно, т.к. направление их в разных точках массива различно. Поэтому радиальное напряжение выражают через составляющие по площадкам, нормальным к осям координат x,y,z, при расположении координатной системы, как показано ниже. Отнесем величину радиального напряжения s _R к горизонтальной площадке, параллельной ограничивающей плоскости (рис.3.9):

а так как то величина радиального напряжения, отнесенного к горизонтальной площадке, равна

. (3.14)

Проектируя величину 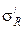по трем взаимно перпендикулярным направлениям и учитывая, что cosb= z/R, получим составляющие напряжения для любой площадки, параллельной ограничивающей плоскости:

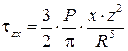,,. (3.15)

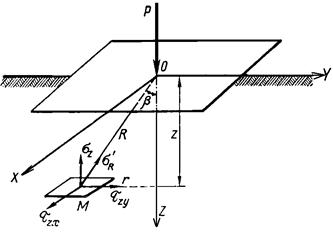
Рис.3.9. Отнесение радиального напряжения к горизонтальной площадке

Составляющие напряжения для площадок, перпендикулярных осям x и y, имеют несколько более сложный вид и зависят от величины коэффициента бокового расширения n₀ и модуля деформации Е ₀.

Наибольшее практическое значение имеют напряжения, действующие на площадке, параллельной ограничивающей плоскости, особенно нормальная составляющая s _z, вызывающая уплотнение грунта. Учитывая, что полярные координаты b и R можно выразить через прямоугольные координаты x, y, z, уравнение для s _z может быть приведено к виду

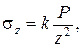(3.16)

где k – коэффициент, зависящий от положения рассматриваемой точки в пространстве,

, (3.17)

где r – расстояние рассматриваемой точки от вертикальной оси приложения нагрузки. Значения k табулированы в зависимости от отношений r/z (табл. II.1 приложения II, пример 1).

Если на поверхности массива действует несколько сосредоточенных сил P ₁, P ₂, P ₃ (рис.3.10), то сжимающее напряжение в любой точке массива можно найти простым суммированием:

, (3.18)

где коэффициент 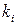определяют по табл. в зависимости от соотношений r_i / z (табл. II.1 приложения II).

Рис.3.10. Схема действия нескольких сосредоточенных сил

Если на поверхности массива приложена местная равномерно распределенная нагрузка на площади ограниченных размеров, то напряжения в любой точке массива могут быть найдены по принципу независимости действия сил как сумма напряжений, возникающих от сосредоточенных нагрузок, заменяющих действие равномерно распределенной нагрузки на элементарных площадках и приложенных в центре тяжести последних (рис.3.11) (пример 2).

Рис.3.11. Схема замены действия равномерно распределенной нагрузки элементарными сосредоточенными силами

Определив величину s _zi от нагрузки каждой площадки, на которые разбита загруженная площадь, и произведя суммирование этих напряжений, найдем напряжение s _z от действия распределенной нагрузки:

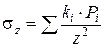. (3.19)

Этот приближенный метод может быть заменен точным интегрированием по всей площади напряжений от нагрузки на бесконечно малый элемент загруженной площади.

Точные решения этой задачи имеют очень сложный вид. В настоящее время получены формулы для определения напряжений под центром загруженного прямоугольника:

max= k ₀ P (3.20)

и для площадок под углом загруженного прямоугольника

s _zc = k_cP, (3.21)

где k ₀ и k_c – табличные коэффициенты, табулированные в зависимости от отношения сторон прямоугольной площадки загрузки a= l/b и относительной глубины рассматриваемой точки (l – длина прямоугольника, b – ширина). Для угловой точки 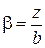(табл. II.2 приложения II, пример 3)

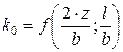, (3.22)

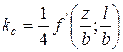. (3.23)

Из формулы (3.23) видно, что угловые напряжения составляют 0,25 от напряжений под центром загруженной площадки.

Дата добавления: 2014-01-07