Нахождение компонент двусвязанности

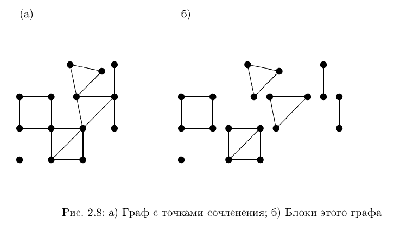
Вершину a неориентированного графа G = (V,E) будем называть точкой сочленения, если удаление этой вершины и всех инцидентных ей ребер ведет к увеличению числа компонент связности графа. Равнозначное утверждение состоит в том, что а является точкой сочленения, если существует вершины v и u, отличные от а, такие, что каждый путь из u в v, а мы предполагаем, что существует по крайней мере один такой путь, проходит черт вершину а. Неориентированный граф называется двусвязным, если он связный и не содержит точек сочленения. Произвольный максимальный двусвязный подграф графа G называется компонентой двусвязанности или блоком этого графа.

Двусвязность графа — очень желательный признак дня некоторых приложений. Представим себе, что вершины графа изображают узлы некоторой информационной сети, а ребра соответствуют линиям передачи. Если наш граф двусвязный, то выход из строя отдельного узла w никогда не приведет к потере соединения между любыми двумя узлами, отличными от w. Знание блоков графа также очень важно, если принять во внимание то, что многие графовые задачи, такие как нахождение всех элементарных циклов или установление факта планарносги графа (граф называется планарным, если его можно так начертить на плоскости, чтобы никакие два ребра не пересекались), приводят естественным путем к аналогичным задачам для блоков данного графа.

Отметим, что если (V1,Bi), (v2,В2) - два разных блока графа G, то V1 ∩ V2 = или V1 ∩ V2 = {а}, где а — точка сочленения графа G. Действительно, рассмотрим подграф (V1 U V2, В1 U В2). Если было бы |V1 ∩ V2| >= 2, этот подграф был бы двусвязным вопреки предположению о максимальности (V1,V2) и (V2,B2). Невозможен также случай VI ∩ V2 = {а}, где a не является точкой сочленения графа G. Ибо тогда в G существует путь между вершинами u є V1, и u ≠ a и u є V2, v ≠ a, не включающий вершину а. Нетрудно отметить, что подграф, возникающий из {V1 U V2,В1 U B2) добавлением вершин и ребер этого пути, будет двусвязным, что противоречит предположению о максимальности (V1,B2) и (V2,B2). На рис. 2.8 дан пример графа, имеющего точки сочленения и блоки.

Нахождение точек сочленения и блоков графа является классической задачей, которую можно эффективно решить погружением в процедуру поиска в глубину (см. Тарьян [66]). Прежде чем представить частный алгоритм, сделаем предварительно несколько замечаний.

Теорема 2.10. Пусть D = (V, T) - стягивающее дерево с корнем r связного графа G = (V,E), построенное, с помощью поиска в глубину (алгоритм 2.3). Вершина v є V является точкой сочленения графа G тогда и только тогда, когда либо v = r u r имеет по крайней мере двух сыновей в D, либо v ≠ r и не связаны ребром ни с одним предком вершины v.

Доказательство. Рассмотрим сначала случай v = r. Если вершина v имеет только одного сына (либо является изолированной вершиной), то ее устранение не увеличит числа компонент связности, ибо это не нарушает связности дерева. Если она имеет по меньшей мере двух сыновей, то после удаления вершины v эти сыновья лежат в разных компонентах связнности. Действительно, из теоремы 2.4 вытекает, что каждый путь между двумя различными сыновьями должен проходить через корень — в противном случае он содержал бы хорду {u,t}, где ни u не является потомком t, ни t не является потомком u. Аналогично, для Случая v ≠ r. Если после устранения вершины v существует путь от ее сына w до корня, то, как и в предыдущем случае из теоремы 2.4, следует, что этот путь должен содержать ребро, соединяющее w или некоторого потомка вершины w c некоторым предком вершины u.

Идея алгоритма следующая: ведем поиск в глубину в графе, начиная с некоторой вершины r, вычисляя для каждой вершины u два параметра: WGN[v] и L[v]. Первый из них — это просто номер вершины v в порядке, в котором вершины посещаются при поиске в глубину, начиная с вершины r. Если через D = (V,Т) мы обозначим дерево, соответствующее нашему поиску в глубину, то другой параметр определяет наименьшее значение WGN[u], где u = v или вершина u связана хордой с вершиной v или ее произвольным потомком в D. Параметр L[v] легко вычислить по индукции относительно дерева D, если мы знаем L[w] для всех сыновей w вершины v. Обозначив

имеем L[v] = min{WGN[v],A,B}.

Из теоремы 2.10 следует, что v является точкой сочленения или корнем тогда и только тогда, когда L[w]>=WGN[v] для некоторого сына u вершины v (полагаем, что n>1).

Алгоритм 2.11. (Нахождение компонент двусвязности графа).

Данные: Граф G = (V,Е) без изолированных вершин, представленный списками инцидентности ЗАПИСЬ[ v ], v є V.

Результаты: Множества ребер всех компонент двусвязности.

1. procedure ДВУСВ(v,p);
(*поиск в глубину, начиная с вершины v и полагая, что p является отцом вершины u в этом процессе; параллельно выписываются ребра найденных компонент двусвязности; переменные num, L, WGN, СТЕК - глобальные*)
2. begin num:= num + 1; WGN[ v ]:= num;
3. L[ v ]:= WGN[ v ];
4. for u є ЗАПИСЬ[v] do
5. if WGN[ u ] = 0 then (*вершина u - новая, { v,u } - ветвь*)
6. begin СТЕК <= { v,u }; ДВУСВ(u,v);
7. L[ u ]:=min(L[ v ],L[ u ]);
8. if L[ u ] >= WGN[ v ] then (* v есть корень или точка сочленении z, а верхняя часть стека до { v,u } включительно содержит компоненту двусвязности*)
9. begin (*выписать ребра компоненты двусвязности*)
10. repeat e <= СТЕК; write(e)
11. until e={v,u};
12. write(';')(*знак конца компоненты двусвязности*)
13. end
14. end
15. else (*WGN[ u ]>Q, т.е. u уже была посещена*)
16. if (u ≠ p) and (WGN[ u ] < WGN[ u ]) then⁴ (* ребро { v,u } - хорда и не включается в стек*)
17. begin СТЕК <={ v,u };
18. L[ v ]:=min{L[ v ],WGN[ u ])
19. end
20. end; (*ДВУСВ*)
21. begin (*главная программа*)
22. for и є V do WGN[ u ]:= 0; (*Инициализация*)
23. СТЕК:=; num:=0;
24. for u є V do
25. if WGN[ u ] = 0 then ДВУСВ(u,0)
26. end

Покажем теперь, что вызов процедуры ДВУСВ(v,0) (строка 25) для еще не рассматривавшейся вершины v влечет за собой выделение и фиксирование всех блоков компоненты связности графа, содержащей вершину v. Доказательство проводится методом индукции по числу блоков этой компоненты. Если компонента связности не содержит точек сочленения, то нетрудно отметить, что вызов ДВУСВ(v. 0) приводит к засылке в стек всех ребер этой компоненты, а затем (см. цикл 10) запись этих ребер. Предположим теперь, что наша компонента содержит к > 1 блоков и что алгоритм работает корректно для произвольной компоненты, содержащей менее k блоков. Рассмотрим первое встретившееся ребро { v,u }, такое что L[ u ] >= WGN[ v ] в строке 8. Согласно нашим предыдущим рассуждениям это неравенство означает, что v — корень или точка сочленения. Ни один из потомков вершины u (в дереве поиска в глубину, реализованном соответствующим алгоритмом) не является точкой сочленения, и в результате ребра верхней части стека до { v,u } включительно являются ребрами графа, соединяющими потомков вершины v вместе с самой u, и тем самым создают блок, который выписывается в цикле 10. Модифицируем теперь нашу компоненту, удалив описанный выше блок (не удаляя вершину v). Модифицированная таким образом компонента имеет к - 1 блок, и выполнение для нее процедуры ДВУСВ (v, 0) вызывает в силу индуктивного предположения корректную запись этих блоков. Действия алгоритма для модифицированной компоненты отличаются от действий в случае c исходной компонентой только тем, что для первой встреченной точки сочленения (исходной компоненты) v цикл 4 не выполняется для вершин u, принадлежащих удаленному блоку. Отсюда легко следует, что ДВУСВ (u, 0) корректно определяет все к блоков нашей компоненты связности, а тем самым весь алгоритм корректно определяет все блоки графа.

Оценим теперь вычислительную сложность алгоритма. Циклы 22 и 25 требуют О(n) шагов, причем для второго цикла не учитываются шаги, выполняемые при вызове ДВУСВ(v,0) для каждой еще не рассмотренной вершины. Такой вызов для компоненты связности с n_i вершинами и m_i ребрами требует О(n_i+n_i) шагов, не считая шагов в цикле 10, так как такая процедура ведет в компоненте поиск в глубину, требуя число шагов, ограниченное константой для каждого просматриваемого ребра. Каждое ребро удаляется из стека и попадает в список ребер блока в точности один раз, что дает в сумме О(m) шагов, совершаемых циклом 10 во время его выполнения всего алгоритма. Суммируя все эти слагаемые, получаем и в итоге общую сложность алгоритма, равную O(n+m).

Дата добавления: 2014-01-07