Динаміка гармонічних коливань

Для визначення характеру руху механічної системи необхідно, використовуючи закони динаміки або збереження енергії, отримати рівняння руху системи, і якщо воно приводиться до вигляду 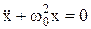, то можна однозначно твердити, що дана система є гармонічним осцилятором, частота w₀ якого дорівнює квадратному кореню з коефіцієнта при х. Розглянемо декілька прикладів і потім узагальнимо отримані результати.

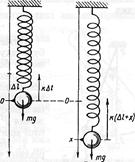Пружній маятник. Нехай кулька маси m підвішена на невагомій пружині жорсткості k, здійснює вертикальні коливання. У положенні рівноваги, в точці О, сила тяжіння зрівноважується силою пружності: (5). Якщо кульку вивести з положення рівноваги і вва­жати додатним напрямом зміщення х від положення рівноваги вниз, то рівняння динаміки для кульки матиме такий вигляд:

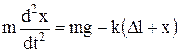, (6)

а враховуючи (5) отримуємо: 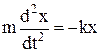, або після перетворення . Легко перевірити підстановкою, що розв'язок цього рівняння виражає гар­монічне коливання 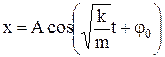з циклічною частотою 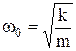і періодом 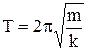. Отже, кулька, підвішена на пружині й виведена з положення рівноваги, перебуватиме в гармонічному коливанні. Характерно, що її коливання не залежить від сили тяжіння, а лише від повертаючої сили пружності, тому вони будуть однаковими в усіх місцях на Землі і навіть на інших планетах.

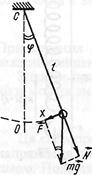Математичний маятник. Математичним маятником називають мате­ріальну точку, підвішену на невагомій і нерозтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння. Нехай маса маятника m, а довжина нитки підві­шування l. З відхиленням маятника від положення рівноваги виникає повертаюча сила 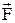: 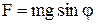, де 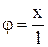– кутове відхилення маятника. Складова зрівноважується реакцією нитки. При малих кутових відхиленнях sinj»j, тому повертаючу силу можна записати у вигляді: 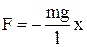, де х – зміщення маятника від положення рівноваги, а знак мінус показує, що повертаюча сила протилежна до напряму зміщення. Враховуючи, що за другим законом Ньютона 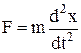, отримуємо: 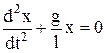, звідки 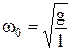. Період коливання математичного маятника: 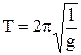. З формули періоду коливання випливають такі закономірності коливання математичного маятника:

- період коливання маятника не залежить від його маси;

- період коливання не залежить від амплітуди;

- період коливання прямо пропорційний квад­ратному кореню з довжини маятника і обернено пропорційний квадратному кореню з прискорення вільного падіння.

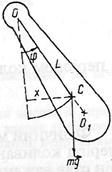Фізичний маятник. Фізичним маятником називають тверде тіло довільної форми, яке коливається під дією тяжіння навколо горизонтальної вісі. Якщо маятник вивести з положення рівноваги, то на нього діятиме повертаючий момент М сили тяжіння, знак якого протилежний знаку кута відхилення маятника, а саме:

,

де L – відстань центра маси від точки підвішування. При малих кутах відхилення 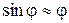(рад) повертаючий момент 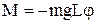. Цей момент надає тілу кутового прискорення: 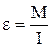. Після відповідних підстановок матимемо рівняння фізичного ма­ятника: , де I – момент інерції тіла відносно осі коливання. Це рівняння цілком аналогічне рівнянню динаміки гармонічного осцилятора. І в цьому разі легко перевірити підстановкою, що роз­в'язок отриманого рівняння задає гармонічне коливання: 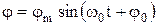з циклічною частотою 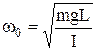і періодом коливання .

Фізичний маятник можна розглядати і як сукупність багатьох математичних маятників різної довжини. Оскільки вони жорстко зв'язані, то короткі маятники спонукають фізичний маятник до частіших коливань, а довгі – до повільніших. Для кожного фізич­ного маятника можна підібрати такий математичний маятник, який матиме однаковий період коливання з даним фізичним. Довжина такого математичного маятника, який має однаковий період з даним фізичним, називається зведеною довжиною фізичного маятника. З рівності періодів коливання цих маятників можна знайти вираз для зведеної довжини l₀ фізичного маятника: 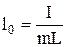. Точка на фізичному маятнику О₁ що відповідає зведеній довжині, називається центром коливань. Центр коливань і точка підвішування – спряжеш точки. Якщо їх поміняти ролями, то період фізичного маятника не зміниться.

Енергія коливального руху. Щоб надати матеріальній точці коливального руху, треба вивести її з положення рівноваги. Для цього виконують певну роботу проти повертаючої сили. Ця робота буде мірою потенціальної енергії, нада­ної точці ззовні: 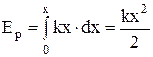. Із отриманого рівняння випливає, що потенціальна енергія точки в коливальному русі пропорційна квадрату її зміщення з положення рівноваги. Після припинення дії зовнішньої сили точка повертатиметься до положення рівноваги під дією квазіпружної сили. У міру зменшення зміщення, відповідно до закону збереження енергії, потенціальна енергія точки перетворюватиметься в кінетичну енергію. Оскільки зміщення точки 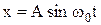і коефіцієнт квазіпружної сили 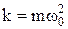, то потенціальну енергію точки в коливальному русі можна визначити за формулою:

.

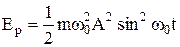Кінетичну енергію точки з масою m і швидкістю v запишемо так:

.

У положеннях крайнього зміщення потенціальна енергія макси­мальна, а кінетична дорівнює нулю. З рухом до положення рівноваги потенціальна енергія зменшується, а кінетична збільшується; у мо­мент рівноваги потенціальна енергія дорівнює нулю, а кінетична набуває максимального значення. Повна енергія точки в коливальному русі складається із суми потенціальної і кінетичної енергії:

,

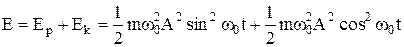або після спрощення: .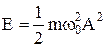

Отже, енергія точки в коливальному русі пропорційна квадрату амплітуди і квадрату частоти. Якщо система ізольована від інших зовнішніх впливів і точка коливається без тертя, то згідно з законом збереження енергія Е коливального руху точки залишається сталою.

Дата добавления: 2014-01-07