Геотермальна енергетика. Геотермальна енергія (природне тепло Землі), акумульована в перших десятьох кілометрах Земної кори, в 10 разів перевищує геологічні ресурси усіх видів палива

Геотермальна енергія (природне тепло Землі), акумульована в перших десятьох кілометрах Земної кори, в 10 разів перевищує геологічні ресурси усіх видів палива разом узятих. Перше місце по виробленню електроенергії з гарячих гідротермальних джерел займає США.

4. Альтернативна гідроенергетика

Приливні електростанції використовують енергію океанських приливів. Найбільша у світі приливна електростанція знаходиться у Франції. 24 турбіни цієї станції забезпечують потужність 240 МВт.

Хвильові електростанції. Електростанції такого типу використовують енергію морських або океанських хвиль. Перша у світі хвильова електростанція потужністю 2,25 МВт була збудована в Португалії в 2008 р.

3.13 Приклади розв’язування задач

1. Імпульс. Закон збереження імпульсу

Той факт, що імпульс тіла є векторною величиною, стане зрозумілим на прикладі розв’язування наступних задач.

1. М’ячик масою 200 г вільно падає з висоти 5м на горизонтальну поверхню. Вважаючи удар абсолютно пружним, визначити зміну імпульсу при такому ударі (рис.3.13.1).

Скорочено умову задачі, що розкриває її фізичний зміст, можна записати у наступному вигляді:

Імпульс тіла (м’ячика) до удару 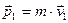, а після удару , тоді векторна зміна імпульсу як векторна різниця дорівнює:

.

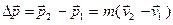В проекціях на вибраний напрям вісі OY модуль зміни імпульсу становить

.

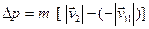Так як удар абсолютно пружний, то швидкість за величиною не змінюється, а змінюється тільки за напрямом, тому можна записати , тому

.

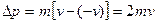Швидкість 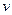, з якою тіло впало на горизонтальну поверхню з висоти – це швидкість вільного падіння 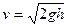, отже

.

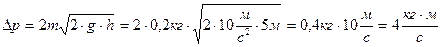Про те, як визначити зміну імпульсу тіла у випадку пружного удару під довільним кутом до поверхні йде мова у наступній1 задачі А саме:

2. м’ячик масою 200 г, що рухається зі швидкістю 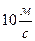до горизонтальної поверхні.Знайти зміну імпульсу м’ячика у випадку абсолютно пружного удар,у якщо кут падіння на поверхню становить 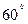(рис.3.13.2.)

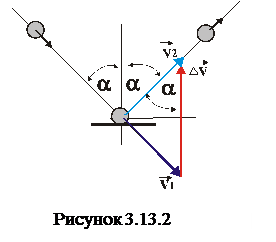
Як і в попередній задачі, зміна імпульсу тіла дорівнює векторній різниці

,

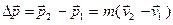де 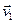– швидкість тіла (м’ячика) до удару, 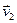- після удару, і, відповідно, векторна різниця цих швидкостей становить вектор:

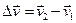
Але за модулем ці швидкості однакові, адже удар абсолютно пружний 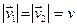і тому 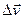, як векторна різниця у даному випадку визначає зміну швидкостей тільки за напрямом.

Нагадаємо, що кути падіння 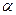чи відбивання відраховуються від нормалі до поверхні та до напряму падіння або відбивання, як це вказано на рис.3.13.2.

Тому з прямокутного трикутника, утвореного вектором швидкості та половиною вектора , маємо:

,

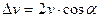і тоді модуль зміни імпульсу даного тіла при куті падіння 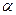дорівнює:

.

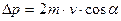Підставивши числові значення величин, що входять у цю кінцеву формулу, отримаємо .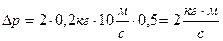

Що стосується задач на закон збереження імпульсу, то їх можна окремо виділити як задачі про абсолютно пружний та абсолютно непружний удари. Непружний удар або непружна взаємодія, у свою чергу, спостерігаються при з’єднанні тіл, тобто коли вони після взаємодії рухаються як одне ціле або при роз’єднанні тіл, коли частина одного тіла відокремлюється від всього тіла. Тому прикладом такого з’єднання будуть дві наступні задачі.

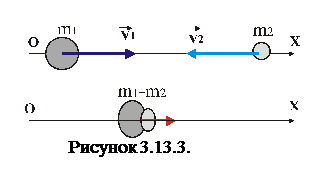
3. Два тіла рухаються назустріч одне одному з швидкостями 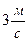. Після абсолютно непружного удару ці тіла стали рухатись разом з швидкістю . Визначити відношення мас цих тіл.

Дано:

два тіла

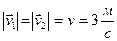, напрями протилежні

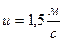після непружного удару

----------------------------------------

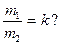
До удару імпульс системи дорівнює

.

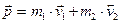Після абсолютно непружного удару тіла рухаються як одне ціле масою 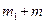з швидкістю , так що імпульс тіл після такого непружного удару становить:

.

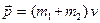Тоді, згідно закону збереження імпульсу:

.

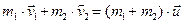Переходячи до проекцій на вибраний напрям (вісь ОХ) та враховуючи числові дані умови задачі, можна записати .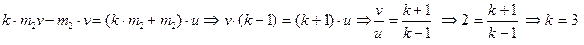

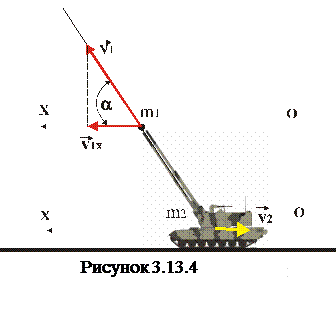
4. З самохідної гарматної установки загальною масою 8 т вистрілюють снаряд масою 5 кг зі швидкістю 1200 м∕ с під кутом 60⁰ до горизонту. Визначити швидкість віддачі установки.

Дано:

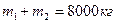загальна маса

двох тіл;

відокремлюється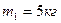

зі швидкістю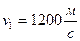

під кутом 60⁰ горизонту.

--------------------------------

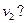
До пострілу імпульс системи (гармата + снаряд) дорівнює нулю. Система замкнута, тому після взаємодії її імпульс зберігається (теж дорівнює нулю):

,

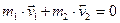звідки

.

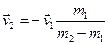Знак «мінус» вказує на протилежний напрям швидкості другого тіла (гармати).

В проекція на вибраний напрям (вісь ОХ) і, враховуючи, що 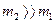, будемо мати

.

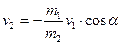Підставляючи числові значення, отримаємо, що модуль швидкості віддачі даної гармати при такому пострілі дорівнює:

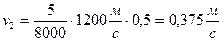м.

Розглянута задача про віддачу при пострілі – це, по суті, задача про реактивний рух. Але в ракетах маємо справу з реактивним рухом тіла змінної маси, адже при згоранні палива маса ракети зменшується. Тому пропонується розв’язати наступну задачу. Будемо самі конструкторами космічних кораблів.

Необхідно вивести на навколоземну орбіту одноступеневий космічний апарат масою 500 кг, надавши йому першої космічної швидкості 7,91 км∕ с. Яка для цього потрібна маса палива, якщо швидкість витікання газів, що утворюються при його згорання дорівнює 2 км∕ с.

Згідно рівняння Ціолковського

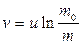
визначимо необхідну масу палива, яка забезпечить при згоранні необхідну швидкість ракеті:

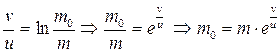
Підставивши всі числові значення величин, наведених в умові задачі, отримаємо:

.

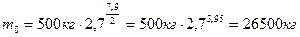Строго кажучи, в ці 26500 кг входить і маса ракети. Тому маса палива буде становити 26500 кг–500 кг = 26000 кг, тобто 26 т, і це за умови стовідсоткового коефіцієнта корисної дії двигунів ракети, який насправді не перевищує 50%.

Щоб більш глибоко зрозуміти закони збереження, доцільно розглянути наступну задачу, в якій присутні всі приклади законів збереження. Надалі побачимо тут непружний удар, закон збереження імпульсу, кінетична і потенціальна енергія та закон збереження і перетворення енергії.

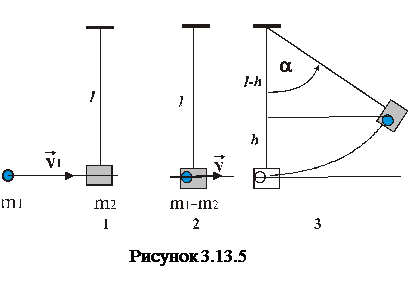Тіло (кулька) масою рухається зі швидкістю 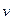і попадає у дерев’яний брусок масою 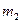та застрягає у ньому. Брусок підвішений на невагомій нитці довжиною . Після такого удару нитка з бруском відхиляється від вертикалі на кут 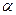. Встановити зв’язок між всіма величинами, які характеризують дану систему, наприклад визначити максимальний кут відхилення нитки від вертикалі.

1. До удару імпульс системи визначається тільки імпульсом першого тіла. Друге тіло (брусок) нерухоме (рис.3.13.5):

.

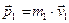2. У результаті непружного удару, коли перше тіло (кулька) застрягає у другому (позиція 2 рис.3.13.5), тіла рухаються як одне ціле з швидкістю 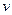так, що імпульс системи дорівнює:

.

Згідно закону збереження імпульсу:

,

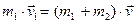звідки модуль швидкість тіл після удару становить:

і їх кінетична енергія дорівнює

.

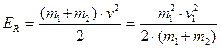3. При подальшому русі системи її кінетична енергія переходить у потенціальну і на висоті , яка відповідає максимальному відхиленню, потенціальна енергія 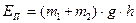дорівнює кінетичній енергії. Прирівнюючи значення цих енергій, отримаємо, що після такої непружної взаємодії два тіла, як одне ціле, піднімуться на висоту від свого попереднього положення:

.

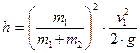Що стосується кута відхилення 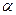, то його можна визначити з простих геометричних співвідношень:

.

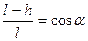Підставивши значення висоти , отримаємо:

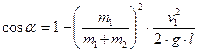
Застосування законів збереження не тільки спрощує розв’язування багатьох задач, але дозволяє зрозуміти суть фізичних явищ, про які йде мова у задачах. У попередніх розділах кінематики та динаміки були наведені приклади такого застосування законів збереження. Наприклад, задача з кінематики про рух тіла, кинутого під кутом до горизонту, дуже просто розв’язувалась застосуванням закону збереження і перетворення енергії (див.1.6.4). Цей самий закон збереження і перетворення енергії дозволив без інтегрального обчислення розв’язати задачу динаміки про визначення швидкості шнура, який зісковзує зі столу (див.2.7, задача 3). Так само значно спрощувалась задача динаміки руху тіла по похилій площині (див.2.7, задача 4).

3.14 Контрольні питання

1. Яка фізична величина називається імпульсом матеріальної точки? Яка формула запису такого імпульсу?

2. Як вивести закон збереження імпульсу і як цей закон формулюється та записується?

3. Яка властивість простору лежить в основі закону збереження імпульсу?

4. Що собою являє центр мас системи? Як визначити положення центра мас системи?

5. Про яку основну властивість центра мас системи йде мова в теоремі про рух центра мас системи?

6. У чому полягає принцип реактивного руху?

7. Як записується рівняння Ціолковського і який його фізичний зміст?

8. Що Ви знаєте про роботи українського вченого Кондратюка Ю.В. в теорії реактивного руху?

9. Які Вам відомі приклади реактивного руху у живій природі?

10. Як дати означення роботи як фізичної величини? В яких одиницях вимірюється робота?

11. Який принцип визначення роботи змінної сили?

12. Як вводиться поняття потужності та в яких одиницях вона вимірюється?

13. Який загальний підхід до поняття енергії як фундаментальної фізичної величини? Яке найбільш загальне означення енергії?

14. Як вивести формулу кінетичної енергії матеріальної точки або тіла при поступальному русі?

15. Як довести, що робота сил тяжіння при переміщенні матеріальної точки не залежить від траєкторії переміщення?

16. Як вводиться поняття потенціальної енергії тіла у полі тяжіння?

17. Як формулюється і записується закон збереження і перетворення енергії?

18. Які системи називаються консервативними і дисипативними? Яка, з точки зору законів збереження, між ними різниця?

19. Як застосувати закони збереження до абсолютно пружного удару двох тіл?

20. Як застосувати закони збереження до абсолютно пружного удару двох тіл?

21. Які основні напрями альтернативної енергетики?

4 ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА ВІДНОСНО НЕРУХОМОЇ ОСІ ОБЕРТАННЯ

Питання динаміки обертального руху твердого тіла мають надзвичайно важливе значення. Тому необхідно встановити найбільш загальні закони динаміки цього руху. Спочатку будемо розглядати найпростіший обертальний рух тіла – обертання відносно нерухомої осі обертання. В принципі, динаміку обертального руху можна описати на основі ІІ закону Ньютона. Для цього тіло треба розбити на такі малі елементи, щоб їх вважати матеріальними точками і визначити сили, що діють на кожен елемент. Але є більш простий метод, метод що базується на законах збереження. Тому розгляд динаміки ючи енергетичні співвідношення, встановимо основні закони цього руху.

4.1 Кінетична енергія обертального руху твердого тіла відносно нерухомої осі обертання. Момент інерції тіла

Нехай тіло довільної форми обертається навколо нерухомої осі обертання (рис.4.1.1). Для поступального руху тіла швидкість всіх точок однакова і кінетична енергія дорівнює 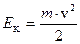. При обертальному русі швидкості різних точок неоднакові. Тому розіб’ємо це тіло на елементи масою 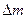, щоб швидкість кожного елемента вважати сталою. На рис.4.1.1 показано -тий елемент на відстані 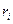від осі обертання, лінійна швидкість елемента .

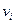Тоді кінетична енергія обертального руху тіла буде дорівнювати сумі кінетичних енергій всіх його елементів:

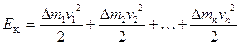. (4.1.1)

Враховуючи зв’язок між лінійною та кутовою швидкостями

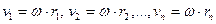, (4.1.2)

отримаємо

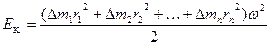. (4.1.3)

Якщо порівняти отриманий вираз з кінетичною енергією тіла при поступальному русі, то бачимо, що замість лінійної швидкості 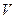маємо кутову швидкість 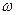, а замість маси 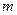вираз в дужках. Як назвати цей вираз? В динаміці обертального руху прийнята своєрідна термінологія. Всі „подібні” величини динаміки обертального руху називаються так, як для поступального тільки з приставкою „момент”. Далі буде показано, що для поступального руху маємо силу, а для обертального – момент сили, при поступальному – імпульс, а при обертальному – момент імпульсу. Отже, якщо для поступального руху маса – міра його інертності, то для обертального руху вираз в дужках, назвали момент інерції як міра інертності тіла при обертальному русі. Момент інерції тіла позначається буквою І. З 4.1.2 випливає, що момент інерції тіла дорівнює сумі моментів інерції всіх його точок:

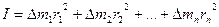, (4.1.4)

або

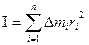. (4.1.5)

Ввівши момент інерції тіла, кінетична енергія його обертального руху з кутовою швидкістю 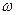відносно нерухомої вісі обертання буде рівна

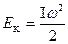. (4.1.6)

Тіло, що обертається, наприклад колесо, може котитися (рис.4.1.2). Тоді кінетична енергія такого руху дорівнює сумі кінетичної енергії обертального руху та кінетичної енергії поступального руху – центра мас тіла:

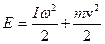. (4.1.7)

4.2 Основне рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання

Як вже раніше говорилось, для опису динаміки обертального руху твердого тіла можна використовувати ІІ закон Ньютона для кожної точки тіла. Але є значно простіший інший метод, який базується на енергетичних співвідношеннях. А саме, до тіла в деякій точці прикладемо силу , яка буде „крутити” тіло і виконана робота піде на збільшення кінетичної енергії обертання цього тіла. Математично описуючи це явище, отримаємо відповідні динамічні співвідношення. Така ідея виводу.

Розглянемо тверде тіло, яке може обертатися навколо нерухомої осі, яка проходить через точку 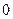і перпендикулярна до площини (рис.4.2.1). У точці 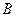на відстані 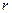прикладена сила , що обертає це тіло.

Сила може змінюватись за величиною і напрямом. Тому розглянемо таке мале переміщення , точки прикладання сили, щоб її вважати сталою, тоді елементарна робота цієї сили дорівнює:

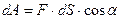. (4.2.1)

При обертальному русі для всіх точок тіла є однаковими кутові кінематичні величини, тому враховуючи, що , будемо мати:

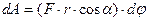. (4.2.2)

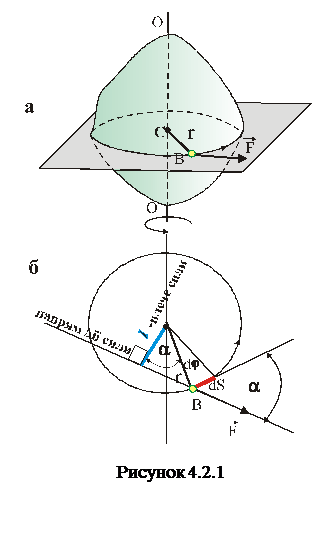
Опустивши перпендикуляр на напрям, маємо, що довжина цього перпендикуляру дорівнює:

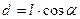. (4.2.3)

Ця найкоротша відстань від осі обертання тіла до напряму дії сили отримала назву момент сили , а добуток сили на плече називається моментом сили:

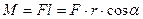. (4.2.4)

Треба зауважити, що при такому означенні моменту сили маємо на увазі момент сили відносно нерухомої осі і такий момент сили є скалярною величиною.

Ввівши поняття моменту сили, вираз елементарної роботи прийме вигляд:

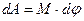. (4.2.5)

За рахунок цієї роботи змінюється кінетична енергія обертального руху даного тіла

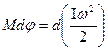. (4.2.6)

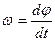Враховуючи, що , а , то

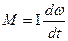. (4.2.7)

Так як 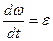, то

(4.2.8)

або .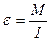

Отримали рівняння, яке називається основним рівнянням динаміки обертального руху твердого тіла відносно нерухомої осі обертання у скалярній формі.

Кутове прискорення тіла при його обертальному русі відносно нерухомої осі обертання пропорційне прикладеному до цього тіла моменту сили і обернено пропорційне моменту інерції цього тіла.

Якщо порівняти це рівняння з ІІ законом Ньютона, то бачимо, що замість лінійного прискорення 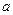маємо кутове прискорення 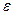, замість сили , момент сили , а роль маси 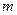грає момент інерції тіла 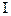. Отже, момент інерції тіла є мірою інертності тіла при його обертальному русі відносно зміни кутової швидкості.

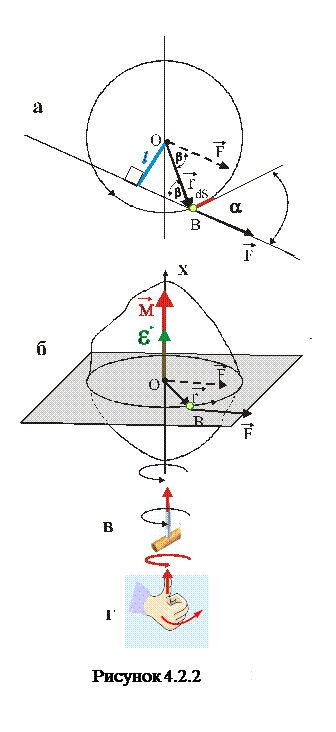Так, як кутове прискорення вектор, то в динаміці обертального руху момент сили, що надає кутового прискорення тілу теж повинен бути вектором. Ще раз звертаючись до рівнянь 4.2.3 та 4.2.4 бачимо, що плече сили – це просто відстань, а момент сили – добуток модуля сили на цю відстань. А тепер перейдемо до векторного опису динаміки обертового руху тіла. Як і у попередньому випадку, сила 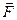, прикладена у точці В, але у даному випадку ця точка прикладання сили визначається радіусом-вектором . Якщо здійснити паралельне перенесення вектора 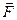(на рисунку 4.2.2 це показано пунктиром), то бачимо, що – це кут між вектором сили і радіусом-вектором, який визначає точку прикладання сили. Тоді плече сили у рівнянні 4.8 можна виразити не через кут 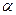, а через кут :

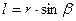, (4.2.9)

у результаті чого модуль моменту сили буде дорівнювати:

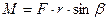. (4.2.10)

Згадаємо елементарну векторну алгебру – скалярний добуток двох векторів визначається через косинус кута між ними, а модуль векторного добутку – через синус такого кута. Так що вираз 4.2.4 немає ніякого відношення до добутку векторів, адже у цьому виразі кут 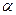– це не кут між векторами, а кут між напрямом сили і переміщенням точки прикладання сили. Зовсім інша справа – співвідношення 4.2.10, де входить синус кута між векторами сили та радіуса-вектора, тобто це співвідношення не що інше, як модуль векторного добутку цих векторів. Тепер залишається вияснити, як записати векторний добуток: 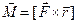чи 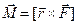, адже від цього залежить напрям вектора моменту сили. Якщо для поступального руху тіла вектор його лінійного прискорення співпадає з напрямом вектора сили, то при обертовому русі тіла напрям кутового прискорення повинен визначатись напрямом вектора моменту сили. Якщо уважно розглянути рис.4.2.2 б, де вказані напрями векторів кутового прискорення та моменту сили, то лише векторний добуток вигляду

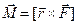(4.2.11)

задовольняє цій умові. Справді, користуючись правилом свердлика (правий гвинт), як вказано на цьому ж рисунку (позиція б), поступальний рух свердлика при даному напрямі обертання вказує напрям вектора моменту сили або можна застосувати правило правої руки (позиція г). Отже, у векторному виді основне рівняння динаміки обертового руху твердого тіла прийме наступний вигляд:

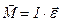. (4.2.12)

Ввівши поняття моменту імпульсу, як буде показано далі, прийдемо до найбільш загального формулювання основного рівняння динаміки обертального руху у векторній формі.

4.3 Момент імпульсу. Закон збереження моменту імпульсу

Враховуючи, що кутове прискорення тіла при обертовому русі дорівнює 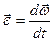, основне рівняння динаміки обертового руху (4.2.12) запишеться:

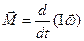, (4.3.1)

подібно як записується другий закон Ньютона .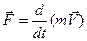

Якщо для матеріальної точки або тіла при поступальному русі величина 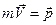називається імпульсом тіла, то при обертовому русі маємо величину, яка дорівнює добутку моменту інерції тіла на його кутову швидкість і ця величина називається моментом імпульсу тіла і позначається :

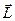. (4.3.2)

і тоді основне рівняння динаміки можна записати:

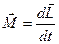. (4.3.3)

Отже, у векторній формі основне рівняння динаміки обертального руху стверджує:

Векторна зміна моменту імпульсу тіла при його обертальному русі пропорційна вектору моменту сили, прикладеного до тіла і відбувається у напряму дії цього моменту сили ( порівняйте з формулюванням другого закону Ньютона через зміну імпульсу ).

В розділі 3.1 було показано, що для замкнутої системи виконується закон збереження імпульсу. Аналогічний закон маємо і для моменту імпульсу:

Якщо на систему тіл, які обертаються, не діють зовнішні моменти сил або їх векторна сума дорівнює нулю, то момент імпульсу системи залишається сталою величиною:

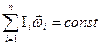(4.3.4)

Справді, якщо для замкнутої системи 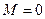, то 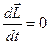, звідки 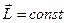(хоча це не строгий вивід закону збереження моменту імпульсу).

В основі збереження моменту імпульсу лежить ізотропність простору, що значить однаковість його властивостей в усіх напрямах. Тут однаковість слід розуміти, що поворот замкнутої системи, як цілого, не змінює її механічних властивостей.

Закон збереження моменту імпульсу можна продемонструвати відомим дослідом – людина на лаві Жуковського, який ілюструє рис.4.3.1.

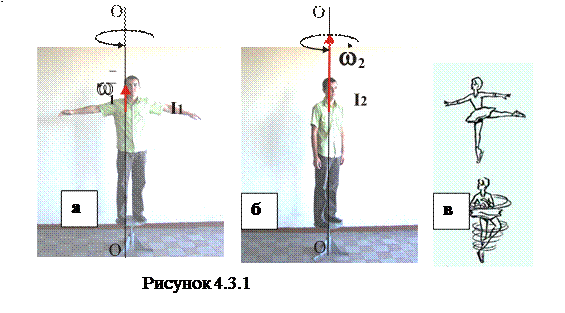Лава Жуковського – це горизонтальна кругла платформа, яка з малим тертям у підшипниках може обертатись навколо вертикальної осі.

а) На лаву Жуковського стала людина, розвела руки у сторони і її «крутнули», надаючи кутової швидкості 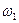відносно вертикальної осі обертання. Тоді момент імпульсу людини дорівнює

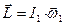, (4.3.5)

де 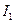– момент інерції людини з розведеними руками (точніше, момент інерції системи людина +платформа).

б) Продовжуючи обертатись, людина опускає руки, так що момент інерції системи зменшується до 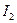. Так як система замкнута (людину вже ніхто не крутить, а тертя при обертанні дуже мале), то, згідно закону збереження моменту імпульсу, зменшення моменту інерції до 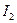приведе до збільшення кутової швидкості до :

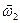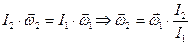. (4.3.6)

в) Одним з елементів фігурного катання на ковзанах є обертання, коли фігурист при обертанні опускає руки, що приводить до його швидкого обертання, як це вказано на рисунку. Тут теж має місце закон збереження моменту імпульсу. Подібно, як на лаві Жуковського, опускання рук спортсмена зменшує його момент, внаслідок чого зростає кутова швидкість фігуриста.

Можна привести ще інші приклади закону збереження моменту імпульсу, що мають значне практичні значення. Наприклад, гелікоптер, має один несучий гвинт, який обертається з великою кутовою швидкістю 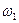(рис.4.3.2). Тоді, згідно закону збереження моменту імпульсу, гелікоптер почне обертатись у протилежному напрямі з кутовою швидкістю :

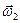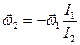, (4.3.7)

де 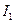– момент інерції гвинта, 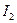– момент інерції гелікоптера. Погодьтесь, керувати гелікоптером, що обертається, справа не з легких. Тому на «хвості» гелікоптера встановлюється додатковий гвинт, що обертається у перпендикулярній до несучого гвинта площині. Цей додатковий гвинт, створюючи силу тяги при плечі цієї сили і відповідним моментом сили 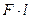компенсує реактивний обертовий момент гелікоптера.

Фундаментальність закону збереження моменту імпульсу дозволила передбачити існування нової елементарної частинки. Так, була відома реакція перетворення нейтрона в протон. Нейтрон перетворюється в протон „викидаючи” з себе електрон. Розглядаючи фізику елементарних частинок буде сказано, що протон, нейтрон та електрон володіють власним моментом імпульсу, який характеризується спіновим числом 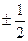(спін – від англ. обертатись). Так ось, якщо в мікросвіті виконується закон збереження імпульсу, то спінове число 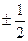до розпаду нейтрона повинно бути рівне сумі спінових чисел протона і нейтрона, які утворились після розпаду, тобто , але така рівність неможлива, значить повинна бути ще одна частинка, спін яка дорівнює 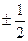. Цю теоретично передбачену частинку назвали нейтрино, яка лише згодом була виявлена експериментально.

4.4 Моменти інерції різних тіл. Теорема Штейнера

Визначення моменту інерції різних тіл надзвичайно важлива практична задача, особливо в техніці, де присутні обертові рухи деталей та механізмів. Для матеріальної точки момент інерції дорівнює добутку маси 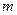на квадрат відстані до осі обертання 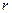, , 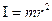а момент інерції тіла – сумі моментів інерцій всіх матеріальних точок. Математично момент інерції тіла відносно заданої осі знаходиться наступним чином. Спочатку тіло розбивається на нескінченно малі елементи масою , щоб вважати їх матеріальними точками. Елементарний момент інерції точки такої маси на відстані 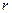від осі обертання дорівнює:

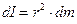. (4.4.1)

Тоді момент всього тіла визначається як інтегральна сума моментів інерцій всіх його матеріальних точок:

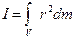. (4.4.2)

Як це робиться, покажемо на окремих прикладах визначення моменту інерції деяких тіл правильної геометричної форми.

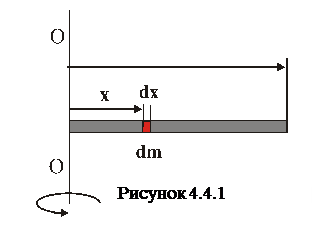1. Момент інерції однорідного стержня масою 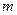і довжиною відносно осі, яка проходить перпендикулярно до його кінця (рис.4.4.1).

Виберемо такий малий елемент , щоб його вважати матеріальною точкою масою 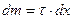, де – лінійна густина – маса одиниці довжини, 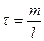(кг/м), тоді

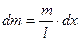, (4.4.3)

а момент інерції такого елемента дорівнює:

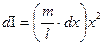. (4.4.4)

Момент інерції всього стержня визначиться інтегральною сумою:

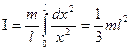(4.4.5)

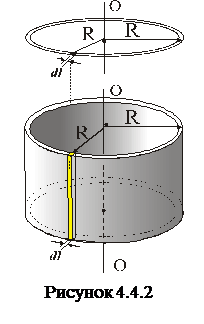2. Момент інерції тонкого кільця або тонкостінного циліндра відносно осі, що проходить через центр.

Як і для попереднього прикладу з однорідним стержнем, тепер уже на кільці (рис.4.4.2а) виділяємо елемент 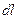, маса якого як матеріальної точки дорівнює 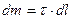. Лінійна густина кільця загальною масою 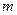і радіуса 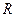визначається як відношення 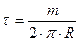. Таким чином, момент інерції виділеного елемента дорівнює:

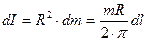. (4.4.6)

Сумарний момент інерції кільця знайдеться інтегральною сумою

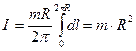. (4.4.7)

Що стосується моменту інерції тонкостінного циліндра (рис.4.4.2б), то очевидно, що його момент інерції дорівнює сумі моментів інерції тонких кілець, які, по суті, утворюють тонкості ний циліндр, тобто:

, (4.4.8)

де 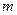– маса всього циліндра.

3. Момент інерції однорідного диска або циліндра

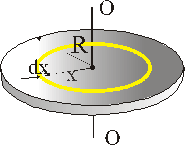У даному випадку однорідний диск можна уявити як сукупність тонких кілець. Тому знаходження моменту інерції однорідного диску зведеться до знаходження інтегральної суми моментів інерцій кілець, з яких складається такий диск. Якщо маса елементарного кільця , а радіус 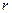, то його момент інерції становить

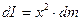. (4.4.9)

Ввівши поняття поверхневої густини кільця, як масу одиниці площі (кг∕м²) при площі кільця ,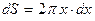

маса такого елементарного кільця буде рівною:

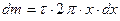. (4.4.10)

В свою чергу, загальній площі диску 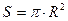та його масі 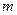поверхнева густина визначиться наступним співвідношенням:

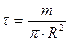. (4.4.11)

Отже,

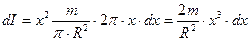. (4.4.12)

Загальний момент інерції диску дорівнює інтегральній сумі (4.4.13) елементарних моментів інерцій кілець, з яких складається цей диск, причому радіус 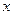таких кілець змінюється від нуля до радіуса 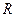диску:

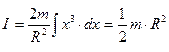. (4.4.13)

4. Момент інерції конуса

Якщо уявити конус як сукупність тонких дисків змінного радіуса, то, відповідно, момент інерції конуса дорівнює сумі моментів інерцій таких дисків, що утворюють даний конус. Так, на рис.4.4.4 зображено конус, де його складовою частиною є диск радіуса 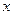та товщиною 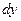. Об’єм такого елементарного диску дорівнює

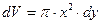. (4.4.14)

Знаючи густину 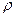речовини конуса, маса такого диску становитиме

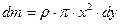. (4.4.15)

Густину речовини диска можна визначити з елементарного співвідношення

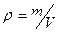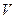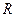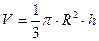, де – об’єм диска, виражений через радіус його основи та – висоту, дорівнює , отже,

. (4.4.16)

Тоді момент інерції 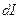такого елементарного диска дорівнює 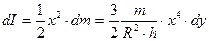. (4.4.17)

Момент інерції всього конуса дорівнює інтегральній сумі моментів інерцій всіх дисків, на які ми розбили цей конус:

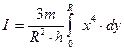. (4.4.18)

Приведемо підінтегральний вираз до однієї змінної, виходячи з подібності трикутників 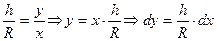і, крім того, для спрощення розрахунків виберемо початок системи координат у вершині конусу, тому

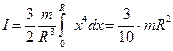. (4.4.19)

5. Момент інерції однорідної суцільної кулі

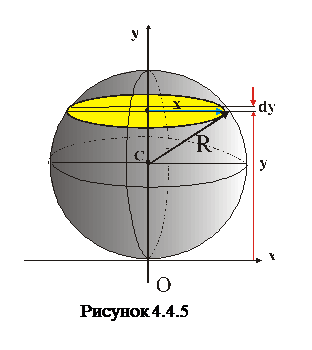Визначаючи момент інерції конуса, ми, по суті, «різали» цей конус на тонкі диски. Користуючись цим самим принципом, «розріжемо» суцільну кулю на нескінченно тонкі диски (подібно як лимон чи апельсин ріжуть на круглі дольки). На рис.4.4.5 показано суцільну куля радіуса 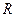з її однією «долькою» – диском радіуса 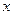і товщиною 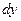. Маса такого елементарного диска визначається співвідношенням 4.4.15. Що стосується густини кулі, то 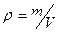, де 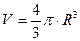– об’єм кулі, тому маса виділеного елементарного диску становить:

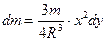, (4.4.20)

а момент інерції дорівнює

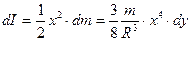. (4.4.21)

Приведемо праву частину цього рівняння до одної змінної враховуючи, що

, (4.4.22)

тоді

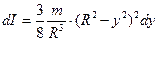, (4.4.23)

Момент інерції всієї кулі дорівнює сумі моментів інерцій всіх елементарних дисків, починаючи від нульового радіусу (точка О на рис.4.4.5), потім, проходячи «екватор» радіусу 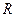, і знову закінчуючи нульовим радіусом на протилежному кінці кулі (ніби на полюсі). Це значить, інтегрування треба проводити у межах: 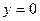(нижня межа), 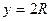(верхня межа):

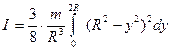. (4.4.24)

Провівши інтегрування, отримаємо, що момент інерції суцільної однорідної кулі відносно осі обертання, що проходить через її центр, дорівнює:

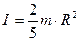. (4.4.18)

6. Момент інерції тонкостінної сфери

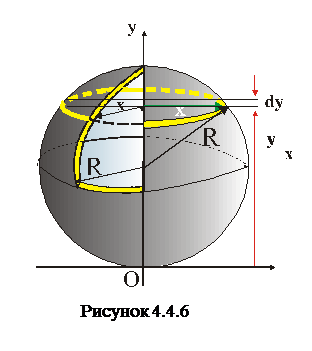Тонкостінна сфера – це тіло сферичної форми, товщина стінок якої значно менша радіуса самої сфери. На рис.4.4.6 показано таку тонкостінну сферу з вирізом, який показує, що всередині сфера порожня. Радіуси зовнішньої та внутрішньої поверхонь тонкостінної практично можна вважати однаковими і якщо цей радіус 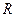, то площа такої сфери дорівнює 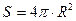. Якщо маса сфери 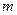, то відношення

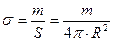(4.4.26)

дає поверхневу густину – масу одиниці її площі – 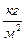. Значення поверхневої густини тонкостінної сфери буде корисним для визначення її моменту інерції. Так, тонкостінну сферу ми будемо «різати» на тонкі смужки радіуса 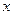, тобто довжиною 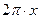, і шириною 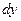– вистою, як вказано на рис.4.4.6. При площі 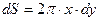такої кільцевої смужки та поверхневій густині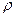її маса дорівнює

. (4.4.27)

Момент інерції виділеного кільця становить

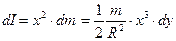. (4.4.28)

Для подальшого інтегрування приведемо праву частину рівняння до однієї змінної, враховуючи, що

. (4.4.29)

Тоді момент інерції даної тонкостінної сфери буде дорівнювати інтегральній сумі моментів інерцій всіх елементарних кілець, де межею інтегрування буде 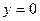, потім, як і для суцільної кулі, переходимо «екватор» радіуса 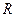і далі виходимо на «верхній полюс», тобто верхня межа інтегрування :

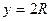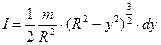. (4.4.30)

Виконавши інтегрування, отримаємо наступний результат – момент інерції тонкостінної сфери відносно осі обертання, що проходить через її центр дорівнює:

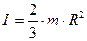. (4.4.31)

Можна було б продовжувати вивід моменту інерції тіл правильної геометричної форми відносно осі обертання, що проходить через їх центр їх мас. Добре, ми потратили час на розрахунок такого моменту інерції відносно осі, що проходить через центр мас тіла, а тіло обертається відносно осі, яка паралельна осі, що проходить через центр мас. Так що, знову починати розбивати тіло на елементарні частини чи то матеріальні точки чи елементарні кільця або диски? Ні, не треба, говорить теорема Штейнера (яку подаємо без доведення). А саме: якщо відомий момент інерції 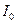тіла масою 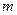відносно осі обертання ОО, яка проходить через центр маси тіла (точка С), то момент інерції 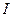цього ж тіла відносно паралельної осі 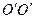на відстані (рис.4.4.7).

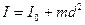. (4.4.32)

4.5 Вільні осі обертання тіла. Головні осі інерції тіла. Головні моменти інерції тіла. Поняття про тензор моменту інерції тіла

У більшості випадків ми звикли до того, що тіло, яке обертається, має вісь обертання, яка з чимось зв’язана. Так, вісь обертання коліс автомобіля закріплена з його корпусом (технічна назва – рамою). Вісь обертання гелікоптера – це вал його двигуна, вісь обертання генератора електростанції жорстко зв’язана з самим генератором і т.п. І, напевне, ви знаєте, що у всіх випадках ці тіла, що обертаються, провинні бути «центровані», інакше, як кажуть – все почне «бити». Згадаймо випадок з велосипедним колесом, яке деформоване, зробило „вісімку”. Почнемо його обертати, тримаючи в руках вісь, і відчуємо, як при обертанні воно „б’є”, вісь треба втримувати. А якщо колесо відцентроване, то вісь обертання залишається нерухомою, наші зусилля прикладені лише для того, щоб колесо не впало, а якщо воно і буде падати, то положення осі обертання у просторі залишиться незмінним.

А що, з точки зору фізики, значить колесо «нецентроване», хоча у фізиці такий термін відсутній. Це значить, що центр мас тіла, що обертається, не співпадає з віссю обертання і тому, крім того, що обертається саме тіло, додатково починає обертатись його центр мас і, щоб втримати вісь обертання нерухомою, необхідно прикласти певні зусилля. При обертанні однорідного симетричного тіла його центр мас співпадає з віссю обертання, положення якої у просторі у відсутності зовнішніх сил залишається незмінним і така вісь обертання називається вільною віссю тіла.

Можна довести, що для тіла довільної форми з довільним розподілом мас існують три взаємно перпендикулярні осі, які проходять через центр мас тіла і ці осі можуть бути вільними осями і, у даному випадку, їх називають головними осями інерції.

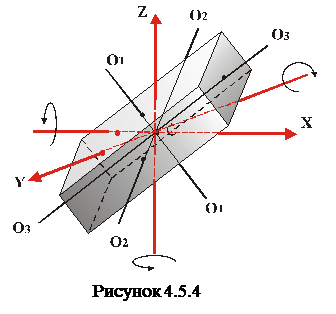
Для однорідного паралелепіпеда головними осями інерції будуть, очевидно, осі О₁О₁ О₂О₂ О₃О₃, які проходять через центри протилежних граней (рис.4.5.1).

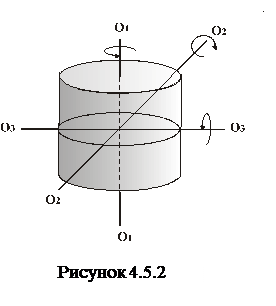
Для тіла, яке володіє осьовою симетрією, наприклад, для однорідного циліндра (рис.4.5.2), однією з головних осей інерції є вісь симетрії – вісь циліндра О₁О₁. Двома другими осями можуть бути дві будь-які взаємно перпендикулярні осі, які лежать в площині, перпендикулярній до осі циліндра і проходять через центр інерції цього тіла. Таким чином, для тіла з осьовою симетрією фіксована тільки одна з головних осей інерції.

Для тіла з центральною симетрією, тобто у кулі чи сфери, головними осями інерції є три будь-які взаємно перпендикулярні осі, які проходять через центр інерції. Тобто, жодна з головних осей інерції не фіксована.

Моменти інерції відносно головних осей інерції називають головними моментами інерції тіла.

У загальному випадку ці моменти інерції різні 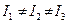. Для тіла з осьовою симетрією два головних моменти інерції мають однакове значення, третій відмінний від них 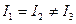. І, нарешті, у випадку тіла з центральною симетрією всі три головних моменту інерції однакові .

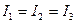Однаковими значеннями моменту інерції володіє не тільки однорідна куля або сфера, але інші тіла, наприклад куб. У загальному випадку така рівність може бути при відповідному розподілі мас тіла довільної форми. Всі подібні тіла називаються кульовими дзиґами ібудь-яка вісь, що проходить через центр симетрії володіє властивостями вільної осі і, відповідно, жодна з головних осей інерції не фіксована подібно як у сфери.

Тіла, для яких 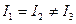, ведуть себе як однорідні тіла обертання і їх називають симетричними дзиґами. Нарешті, тіла з 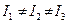– це асиметричні дзиґи.

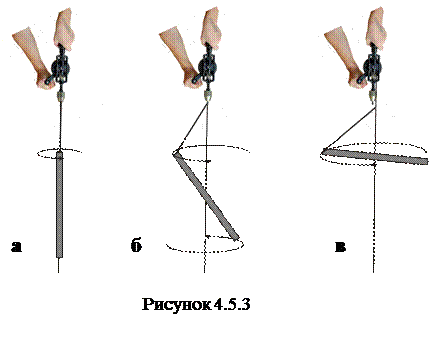
Найбільш стійким положенням при обертанні тіла є його обертання відносно осей, які відповідають максимальному і мінімальному значенню моменту інерції цього тіла.

Наприклад, підвісимо на нитці циліндричний стержень, який будемо розкручувати, збільшуючи його кутову швидкість, як вказано на рис.4.5.3 (розкручуємо ручною дрелькою).

а) Вісь обертання з найменшим моментом інерції співпадає з напрямом підвісу і тоді таке положення тіла (стержня) при його обертанні буде стійким.

б

В дійсності, точне співпадання вільної осі обертання з напрямом підвісу не завжди здійсниме. Тому при навіть незначному неспівпаданні вільної осі з найменшим моментом інерції обертання з підвісом приведе до нестійкого положення обертання. Відцентрові сили відхиляють стержень від вертикального положення.

	в

При подальшому збільшенні кутової швидкості це відхилення стає все більшим, і стержень займає майже горизонтальне положення, обертаючись відносно вільної осі обертання з найбільшим моментом інерції.

Отже, для обертання тіла відносно вільних (головних) осей маємо, що момент імпульсу відносно цих осей визначається наступними співвідношеннями:

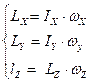(4.5.1)

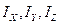де – моменти інерцій відносно осей, що співпадають з головними осями, 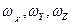– кутові швидкості обертання відносно цих осей. У загальному випадку, коли обертання відбувається відносно довільно орієнтованих осей XYZ зв'язок між компонентами моменту імпульсу стає більш складним:

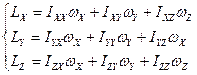(4.5.2)

де 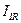– коефіцієнти, які мають розмірність моменту інерції, але «особливого» моменту інерції. Так, перший індекс 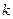«пробігає» три значення і він вказує, відносно якої осі обертання визначається момент імпульсу. Другий індекс теж «пробігає» три значення і показує, відносно якої з осей обертається дана вісь.

Наприклад, про що говорить перше рівняння у виразі 4.5.2? Так, компонента моменту імпульсу 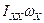стосується обертання тіла відносно осі ОХ з кутовою швидкістю 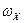відносно цієї ж осі. Але сама вісь ОХ може обертатись з кутовою швидкістю 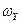відносно осі OY, про що вказує друга компонента 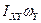. Третя компонента стосується обертання осі ОХ відносно осі OZ з кутовою швидкістю 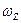. Аналогічно, розкривається фізичний зміст компонент імпульсу в наступних рівняннях, де мова йде про обертання стосовна осей OY та OZ. Так ось, ці «особливі» моменти інерцій, а, точніше, коефіцієнти пропорційності, біля відповідних кутових швидкостей разом визначають момент інерції тіла сукупністю дев’яти величин, які називаються тензором інерції тіла ( тензор від латинського tendere, «тягнутись, простиратися»):

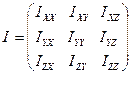. (4.5.3)

Раніше ми розглядали момент інерції у найпростішому випадку – обертання тіла відносно фіксованої осі. Поняття тензора інерції – більш загальне поняття. Знаючи тензор інерції, можна знайти його окремі компоненти, у тому числі відносно фіксованої осі. Такі питання розглядаються в спецкурсах теоретичної фізики та теоретичної механіки, а також в прикладних задах інженерної механіки. Тут лише відмітимо, що діагональні компоненти тензора – це моменти інерції відносно відповідних координатних осей. Ці компоненти називаються осьовими моментами інерції. Якщо координатні осі співпадають з головними моментами інерції, то тензор інерції стає «чисто» діагональним, відсутні недіагональні компоненти

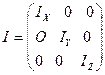. (4.5.3)

4.6 Гіроскопічний ефект. Прецесія гіроскопа

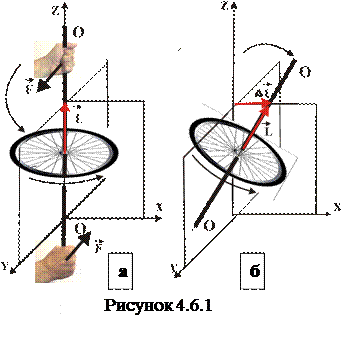
При поступальному русі тіла зміна напряму його руху відбувається у напрямі прикладеної до цього тіла сили. По аналогії, можна чекати такого ж явища і для обертального руху: у якому напрямі хочемо повернути тіло, що обертається так воно і повернеться. Наприклад, велосипедне колесо, як вказано на рис.4.6.1 а, обертається відносно вільної осі ОО, яка співпадає з координатною віссю OZ. Взявши двома руками вісь обертання цього тіла, ми намагаємось повернути цю вісь у площині YOZ. Але при цьому відбуваються «дивні» речі: вісь повертається у перпендикулярному напрямі у площині XOZ (рис.4.6.1 б). Якщо ж повертати вісь обертання колеса у площині XOZ, то вісь обертання знову ж таки повернеться у перпендикулярній площині, тільки тепер у площині XOZ. Таке явище отримало назву гіроскопічного ефекту. Гіроскоп від грецького gyros – коло та skopeo – дивлюсь. Таким чином, гіроскопічний ефект – явище повороту вільної осі обертання тіла у площині, яка перпендикулярна площині прикладання сили або пари сил до вільної осі обертання цього тіла. Причому, цей ефект стає особливо помітним при великих швидкостях обертання. Тому симетричне тіло, що обертається з великою кутовою швидкістю відносно вільної вісі обертання, називають гіроскопом ( від грецького гіро – обертання, скопе – бачити).

Цікаво відмітити, що термін «гіроскоп» вперше запровадив французький фізик Фуко Жан Бернара (1819-1868рр.), назвавши гіроскопом маятник, що демонстрував обертання Землі, дуже влучна назва: такий маятник, який згодом отримав назву маятника Фуко, дійсно давав змогу «бачити» обертання Землі. Під куполом Пантеону у Парижі Фуко підвісив металеву кулю масою 28 кг на стальній дротині довжиною 67м так, що період коливання такого маятника становив 16,4 с. Площина коливання маятника Фуко, як гіроскопа при обертанні Землі, залишалась сталою, а підлога Пантеону, тобто поверхня Землі, оберталась. Зміщення на підлозі сліду від коливань маятника наглядно демонструвало обертання Землі.

Властивість гіро

Дата добавления: 2014-01-07