Метод Стокса

Формула Стокса визначає силу опору при русі тіла сферичної форми у в’язкому середовищі. Отже, вимірявши цю силу для тіла сферичної форми радіуса 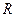, в’язкість середовища, де зі швидкістю 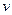рухається дане тіло дорівнює:

. (5.8.23)

У віскозиметрах, де використовується метод Стокса, рух тіла сферичної форми (стальної кульки) здійснюється під дією власної ваги, і такі віскозиметри називаються віскозиметрами з падаючою кулькою.

5.9 Приклади розв’язування задач

З умови нерозривності струмені випливає, що зменшення поперечного перерізу трубки течії рідини приводить до збільшення її швидкості. Тому, з цієї точки зору, найпростіша задача буде мати наступний зміст:

1. Швидкість течії води у широкій частині труби дорівнює 20 см ∕с. Яка швидкість течії у вузькій частині, що має діаметр у 4 рази менший від діаметра широкої частини?

З умови нерозривності струмини

. (5.9.1)

Так як відношення площ кіл пропорційна квадрату відношення їх радіусів або діаметрів,то

. (5.9.2)

Отже,

. (5.9.3)

А тепер зворотна задача – потік рідини не обмежений у прямому розумінні трубою. Потік рідини у залежності від своєї швидкості формує «свою» трубку течії, стає вільною. Прикладом цього є струмина води, яка вільно витікає з отвору. До отвору вона була «затиснута» у трубу, а тепер стає вільною. Прикладом цього може бути фонтан води, який наведено на рис.5.9.1. До речі, цей фонтан є одним з елементів всесвітньо відомого каскаду фонтанів у Петергофі. З рисунку бачимо, що струмина води з збільшенням висоти збільшується у поперечних розмірах. Тому доцільно розглянути задачу про зміну площі поперечного перерізу вертикальної струмини води, а саме:

2. З отвору площею поперечного перерізу 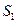зі швидкістю 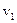у вертикальному напрямі витікає струмина рідин. Якою буде площа поперечного перерізу струмини на висоті ?

З умови нерозривності струмини

. (5.9.4)

Рисунок 5.9.1

Швидкість частинок рідини на висоті можна визначити з кінематичного рівняння

. (5.9.5)

Отже,

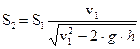. (5.9.6)

Ця формула справедлива лише до верхньої точки струмини рідини. У верхній точці вертикальної струмени рідини відбувається зміна її швидкості на протилежну, відбувається ділення потоку рідини на окремі краплі, де втрачає сенс застосування умови нерозривності.

Поняття умови нерозривності струмини – фундаментальне поняття в задачах механіки рідин і газів, особливо коли йде мова про фізичний зміст добутку: площа поперечного перерізу трубки течії швидкість рідини чи газу = Q (їх об’ємна витрата). Використання такого поняття до застосування рівняння Бернуллі вимагає наступна задача:

3. Повітря продувається через горизонтальну трубку АБ, так що через кожну хвилинну протікає 1 л повітря. Площа поперечного перерізу широкої частини труби дорівнює 2см ² , а вузької 0,5см ². Знайти різницю рівнів 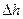води у трубці, що з’єднує дві частини труби АБ. Густина повітря 1,32 кг ∕ м³ .

Різниця рівнів 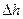води у трубці, що сполучає дві частини трубки течії АБ зумовлена різницею тисків повітря в широкій та вузькій частині трубки течії повітря. Тому скорочений запис умови даної задачі має вигляд: Рисунок 5.9.2

З рівняння Бернуллі для горизонтально розташованої трубки течії ідеальної рідини чи газу:

(5.9.7)

отримаємо

. (5.9.8)

Враховуючи, що

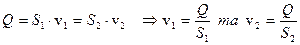
. (5.9.9)

Підставивши числові значення, отримаємо

Так як , то

Рівняння Бернуллі стосується ідеальних рідин і газів, у яких відсутнє внутрішнє тертя (в’язкість). Найпростіший випадок в’язкої течії – це течія в’язкої рідини у круглій трубі, і ця течія описується відповідною формулою Пуазейля. Застосуємо цю формулу для наближеного розрахунку нафтопроводу Одеса – Броди, схему якого наведено на рис.5.9.3.

Нафта танкерами доставляється в так званий термінал (спеціальний причал для розвантаження танкерів), а потім розвантажена нафта поступає на компресорну станцію, яка під високим тиском направляє потік нафти в нафтопровід.

Задача буде стосуватись розрахунку мінімального значення тиску, який забезпечить транспортування нафти від Одеси до Бродів.

Згідно формули Пуазейля, різниця тисків на кінцях нафтопроводу як круглої труби становить

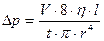. (5.9.10)

Для розрахунків необхідно перевести пропускну здатність нафтопроводу з млн.т. ∕ рік у враховуючи, що , а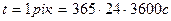

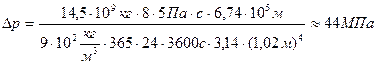. (5.9.11)

У наведеній задачі було використано значення в’язкості нафти . Це значення в’язкості можна отримати дослідним шляхом за допомогою відповідних приладів, які називаються віскозиметрами. В реології для цієї мети найбільшого застосування набули ротаційні віскозиметри. Тому наступна задача ставить своєю метою дати уявлення про теорію та практику ротаційного віскозиметра.

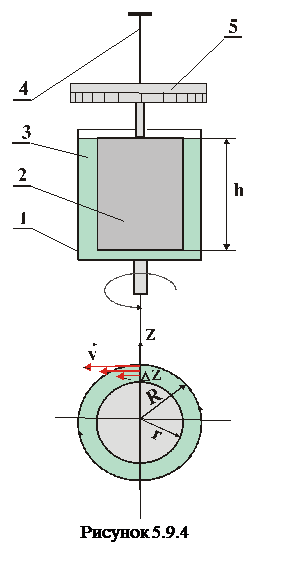
Ротаційний віскозиметр складається з двох коаксіальних циліндрів – зовнішнього 1 радіуса R=4см та внутрішнього 2 радіуса r=3,5см. Між циліндрами знаходиться досліджувана рідина 3. Зовнішній циліндр обертається з кутовою швидкістю і завдяки силам внутрішнього тертя у рідині приводить у рух внутрішній циліндр закручуючи на кут торсіон 4 (пружну нитку), на якому висить цей циліндр. Кут закручування торсіона фіксується за шкалою 5. Модуль кручення торсіона дорівнює . За наведеними числовими значеннями умови задачі визначити коефіцієнт в’язкості введеної у віскозиметр рідини.

Течія між циліндрами віскозиметра можна вважати плоскопаралельною, де швидкість лінійно змінюється у радіальному напрямі на відстані від нуля (внутрішній циліндр) до швидкості точок поверхні зовнішнього циліндра. Тому градієнт швидкості для даної течії дорівнює:

. (5.9.12)

Підставивши це значення градієнта швидкості у закон Ньютона для внутрішнього тертя, отримаємо:

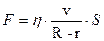. (5.9.13)

Враховуючи зв'язок між лінійною та кутовою швидкостями будемо мати:

. (5.9.14)

Сила внутрішнього тертя, яка приводить в обертання внутрішній циліндр віскозиметра, діє на площу 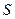, яка дорівнює бічній площі цього циліндра висотою :

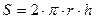. (5.9.15)

Отже,

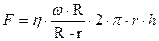. (5.9.16)

Що стосується значення сили , то це значення можна знайти з наступної умови: момент сили внутрішнього тертя дорівнює моменту сили деформації кручення торсіона:

. (5.9.17)

Підставивши це значення в 5.9.16, отримаємо кінцеву формулу для визначення коефіцієнту в’язкості даним ротаційним віскозиметром:

. (5.9.18)

У цій формулі доцільно ввести величину, яку називають сталою віскозиметра

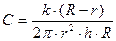. (5.9.19)

Тоді при заданій кутовій швидкості 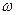обертання зовнішнього циліндра в’язкість досліджуваної рідини дорівнює:

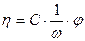. (5.9.20)

Підставивши числові значення, отримаємо наступне значення сталої ротаційного віскозиметра . Тоді при кутовій швидкості і куті закручування торсіона на 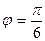в’язкість досліджуваної рідини буде дорівнювати .

Визначення в’язкості цієї ж рідини може бути здійснена методом Стокса, про що йде мова у наступній задачі.

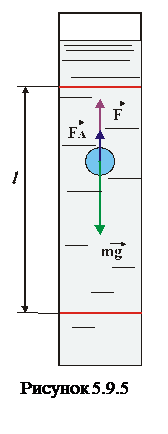
На кульку (рис.5.9.5) діють: сила тяжіння 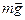, вертикальна виштовхувальна (Архімедова) сила та сила опору (сила внутрішнього тертя). При рівномірному русі кульки рівнодійна цих сил дорівнює нулю або у скалярному вигляді ця умова запишеться так:

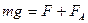. (5.9.21)

Масу кульки можна виразити через її об’єм і густину сталі

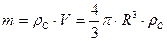. (5.9.22)

Виштовхувальна (Архімедова) сила визначається вагою рідини в об’ємі зануреного тіла (кульки):

. (5.9.23)

Сила за формулою Стокса дорівнює

. (5.9.24)

Отже,

Так як швидкість рівномірного руху кульки 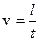, то

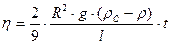
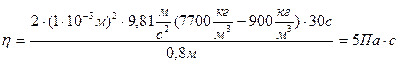
5.10 Контрольні питання:

1. Яке поле називається векторним полем швидкостей?

2. Що собою являють лінії течії рідини або газу?

3. Яке означення трубки течії рідини чи газу?

4. Як вводиться поняття потоку вектора швидкості для однорідного та неоднорідного векторного поля швидкостей?

5. Як записується і формулюється умова нерозривності струмини?

6. Як записується та пояснюється рівняння Бернуллі для ідеальної рідини або газу?

7. Як, користуючись рівнянням Бернуллі, визначити швидкість витікання рідини з малого отвору?

8. Як записується рівняння Бернуллі для горизонтальної трубки течії?

9. Що собою являє трубка Піто і як вона використовується для визначення швидкості потоку рідини або газу?

10. Які приклади застосування рівняння Бернуллі у техніці?

11.Що, з точки зору механіки газів, являє собою циклон і торнадо?

12. У чому полягає явище внутрішнього тертя в рідинах і газах?

13. Як записується і формулюється закон Ньютона для внутрішнього тертя?

14. Який фізичний зміст коефіцієнта динамічної в’язкості?

15. Що собою являє течія Пуазейля. Як записується формула Пуазейля та який її фізичний зміст?

16.Яка різниця між ламінарним і турбулентним режимами течії рідини або газу?

17. Як вводиться поняття чисел Рейнольдса?

18. Як пояснити підіймальну силу крила літака?

19. Як записати і пояснити формулу Стокса для руху у рідині чи газі тіла сферичної форми?

20. Якими питаннями займається реологія як розділ механіки рідин і газів?

21. Які системи називаються ньютонівськими та неньютонівськими?

22. Який вигляд мають реологічні криві бінгамівські пластики, псевдопластики та ділатантні системи?

23. Яка будова і принцип роботи ротаційного віскозиметра?

24. Яка будова і принцип роботи капілярного віскозиметра?

24. Яка будова і принцип роботи віскозиметра з падаючою кулькою?

6 МЕХАНІЧНІ ВЛАСТИВОСТІ ТВЕРДИХ ТІЛ

У попередньому розділі механіки рідин і газів розглядалась механіка суцільних середовищ, де у кожній точці простору присутня речовина. Що стосується механічних властивостей твердих тіл, то найбільш загальні властивості їх деформацій теж можна розглядати як деформацію суцільних середовищ. Тобто, встановлюючи найбільш загальні характеристики деформації тіла, не обов’язково звертатись до його внутрішньої будови. Дійсно, розглядаючи сили пружності на прикладі деформації пружини, ми встановлювали залежність деформації (видовження пружини) від прикладеної сили, а не змін відстані між вузлами кристалічної решітки металу, з якого виготовлена дана пружина. Таким чином, вважаючи тверде тіло суцільним середовищем, деформацію такого тіла описати відповідним зміщенням частинок цього тіла одне відносно одного.

6.1 Основні види пружних деформацій твердого тіла

Найпростіший закон, що описує односторонню пружну деформацію тіла під дією прикладеної до нього сили – це відомий закон Гука. Ще раз нагадаємо цей закон, який говорить, що у межах пружності сила пружності пропорційна зміні лінійних розмірів тіла (видовженню або стисненню тіла). Тому розгляд основних видів деформації почнемо з одностороннього розтягу (або стиску).

1. Одностороння деформація розтягу (стиснення).

Під односторонньою деформацією розуміють таку деформацію, коли змінюються лінійні розміри тіла лише в одному напрямі. Для прикладу розглянемо тіло у вигляді однорідного стержня або циліндра (рис.6.1.1). Деформація (на рисунку це розтяг) відбувається під дією сили F, яка прикладена перпендикулярно до поперечного перерізу стержня і під дією цієї сили довжина стержня змінилась на 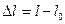, як різниця між кінцевим і початковим значення його довжини. Звичайно, абсолютне значення зміни лінійних розмірів тіла ще не дає уявлень про механічні властивості речовини, з якого виготовлене дане тіло (стержень). Дійсно, нехай 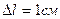, це багато чи мало – залежить від значення початкових розмірів. Тому, описуючи деформацію тіл, вводять поняття відносної деформації. У нашому випадку це відношення абсолютного видовження до початкової довжини :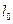

. (6.1.1)

Крім того, відносна зміна лінійних розмірів тіла при одному і тому ж значенні прикладеної сили залежить від площі поперечного перерізу тіла. Не важко переконатись: чим більша площа поперечного перерізу тіла, тим для однакового видовження потрібна більша сила. Тому, математично описуючи зміну лінійних розмірів тіл під дією прикладеної сили F, необхідно ще враховувати площу S поперечного перерізу цього тіла. Відношення сили F, яка прикладена до площі S поперечного перерізу тіла, називається механічне напруження і позначається :

. (6.1.2)

Одиницею механічного напруження є .

У межах пружної деформації відносна зміна лінійних розмірів тіла пропорційна механічному напруженню 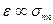. Тепер для знаку рівності необхідний коефіцієнт, який би враховував пружні механічні властивості речовини даного тіла і, звичайно, залежав би від вибору системи одиниць вимірювань. Такий коефіцієнт ввів англійський фізик Юнг і назва цього коефіцієнту – модуль Юнга, позначається буквою Е ( перша буква у слові Expantion – розширення, розтяг). Ввівши такий модуль, закон односторонньої пружної деформації прийме наступний вигляд:

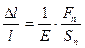(6.1.3)

або

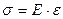. (6.1.4)

З останнього рівняння легко розкрити фізичний зміст модуля Юнга.

Якщо , то 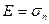, тобто

модуль Юнга Е для речовини даного тіла дорівнює такому нормальному механічному напруженню , яке зумовлює відносну зміну довжини цього тіла, рівну одиниці.

Якщо , то це значить , тобто довжина тіла збільшується у два рази, таким чином модуль Юнга Е для речовини даного тіла дорівнює такому нормальному механічному напруженню , яке зумовлює його видовження у два рази (якщо б при такій деформації виконувався закон Гука).

Зрозуміло, що більшість твердих тіл просто не втримають такого механічного напруження, при якому вони розтягуються вдвічі. Тому у таблицях механічних властивостей різних матеріалів, крім модуля Юнга, вказується максимальне механічне напруження або границя міцності, після якого тіло руйнується.

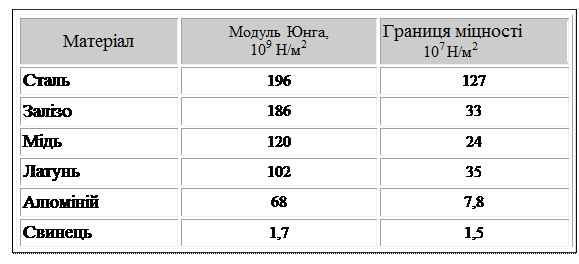
Визначення механічних властивостей різних матеріалів в лабораторних умовах здійснюється за допомогою спеціальних установок, які називаються розривними машинами. Сучасні розривні машини поєднують потужну механічну частину, яка розтягує або стискає досліджуваний матеріал та систему здавачів, що фіксують механічні навантаження і деформації досліджуваного взірця. Інформація від таких здавачів у вигляді електричних сигналів поступає на комп’ютер розривної машини і комп’ютер видає отриману залежність деформації від механічного напруження. На рис.6.1.2 наведено загальний вигляд розривної машини. Досліджуваний взірець розтягується плунжером (поршнем) потужного гідравлічного приводу. На моніторі комп’ютера можна бачити отриману експериментальну криву розтягу з наступними характерними ділянками.

0-1. Ця ділянка відповідає малим відносним змінам лінійних розмірів тіла, при яких справджується лінійний закон пружної деформації Гука. Найбільше напруження, до якого ще має місце закон Гука, називається межею пропорційності.

1-2. Подальше збільшення напруження зумовлює нелінійний характер видовження тіла і після припинення дії механічного напруження тіло вже не відновлює попередню форму.

3-4. Ділянка плинності або течії твердого тіла. Без збільшення механічного напруження має місце збільшення деформації тіла, яке веде себе подібно до рідини, тобто «тече». Якщо прослідкувати за зміною форми тіла, то при такій плинності воно стає тоншим, як це показано на рис.6.1.2.

4-5. При напруженнях, перевищуючих межу текучості, пружні властивості тіла у деякій мірі відновлюються і тіло знову починає чинити опір деформації. Тіло зазнає значних змін форми, утворюється характерне звуження, у якому в подальшому наступає розрив при напруженні, яке визначає границю міцності.

2. Деформація зсуву.

Зсувом називають таку деформацію твердого тіла, при якій всі його плоскі шари, не викривлюючись і не змінюючись у розмірах, зміщаються паралельно один одному (рис.6.1.3). Зсув відбувається під дією дотичної сили, яка прикладена до тіла паралельно площині зсуву. На рисунку 5.1.3 така дотична сила прикладена до верхньої грані тіла, а нижня закріплена нерухомо. Відношення такої дотичної сили до площі 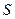шару тіла, яке зазнає деформації зсуву, називається дотичним або тангенціальним механічним напруженням:

. (6.1.5)

І так само, як нормальне напруження чи тиск, вимірюється у паскалях.

Абсолютна деформація зсуву або абсолютний зсув 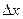визначає лінійне зміщення шару тіла від попереднього положення. Звичайно, що сам абсолютний зсув ще не є повною кількісною характеристикою деформації зсуву всього тіла. Необхідно враховувати відстань між шарами, тобто, ввести поняття відносної деформації зсуву. На рис.6.1.3 відстань 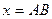– відстань між шарами тіла. При малих зсувах

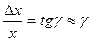, (6.1.6)

і цей кут називають відносним зсувом, і для пружних деформацій він пропорційний дотичному механічному напруженню:

. (6.1.7)

Величина 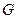, яка визначає пружні властивості тіла при його деформації зсуву, називається модулем зсуву. Якщо , то 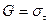. Отже,

модуль зсуву для речовини даного тіла дорівнює такому дотичному механічному напруженню, яке викликало би у цьому тілі відносний зсув, рівним одиниці у випадку пружної деформації.

Деформації зсуву враховуються та розраховуються при конструюванні та виготовлені різноманітних технічних деталей та конструкцій. У природі теж мають місце явища, пов’язані з деформацією зсуву. Так, у геологічних масштабах зсув – сповзання і відрив мас гірських порід вниз схилом під дією тяжіння. Характер і масштаби зсуву можуть бути різними: починаючи від невеликих зсувів (рис.6.1.4) до катастрофічних наслідків, викликаних зсувом величезної маси гори (рис.6.1.5). Особливо небезпечні наслідки мають підводні зсуву гірських порід, які приводять до руйнівних цунамі.

3. Деформація кручення.

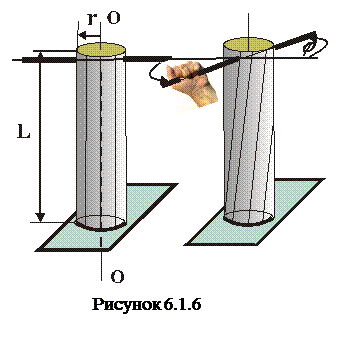Деформація кручення виникає у тілі, якщо один переріз тіла закріплений нерухомо, а на другий переріз діє обертальний момент сили. Наприклад, нижня основа циліндра, як вказано на рис 6.1.6, закріплена нерухомо, а верхній переріз почнемо обертати, так що вісь обертання співпадає з віссю ОО циліндра. (Для зручності обертання у циліндрі біля верхнього перерізу зробимо отвір у який вставимо стержень і ним будемо проводити обертання).

Під дією обертального моменту сили всі поперечні перерізи циліндра повертаються відносно осі ОО на деякі кути, які тим більші, чим далі поперечні перерізи знаходяться від нижнього нерухомо перерізу. Звичайно, що найбільший кут 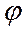буде для верхнього перерізу, і цей кут називається кутом кручення. При деформації кручення має місце паралельний зсув шарів тіла одне відносно одного. Тому розрахунок деформації кручення може бути зведений до розрахунку деформації зсуву. Опускаючи такі розрахунки, кінцева формула, яка встановлює залежність між моментом сили М, який закручує на кут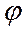однорідний круглий стержень (циліндр) довжиною та радіусом 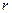має наступний вигляд:

, (6.1.8)

де 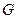– модуль зсуву для матеріалу стержня.

На основі деформації кручення бузуються принципи роботи багатьох вимірювальних приладів. Пружний елемент, що зазнає деформації кручення називається торсіон (від англійського torsion – кручення). Знаючи пружні властивості торсіона і вимірявши його кут закручування, можна визначити момент сили, що закручує цей торсіон. Торсіони з дуже малим значенням модуля зсуву використовуються в надзвичайно чутливих торсійних терезах для визначення маси (точніше ваги) невеликих взірців речовини. Так, на рис.6.1.7 наведено загальний вигляд сучасних цифрових торсійних терезів, які визначають масу тіл з точністю 0,01 мг.

Застосування торсіонів в реології було розглянуто при описі ротаційних віскозиметрів. Більшість електровимірювальних приладів теж використовують торсіони як пружні осі обертання рамки зі струмом у магнітному полі, де деформація кручення торсіона пропорційна електричному струму.

4. Деформація прогину.

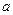Деформація прогину – це вертикальне зміщення точок осі елементів тіла (балки, стержня, циліндра і т.п) під дією сили, яка перпендикулярна осі цього тіла. Як приклад, розглянемо деформацію прогину однорідного стержня довжиною та прямокутним перерізом зі сторонами та 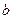(рис.6.1.8 А). Якщо кінці такого стержня знаходяться на двох опорах і до середини стержня прикласти силу , то відбудеться деформація прогину. За такої деформації випуклі частини тіла (на рисунку – верхня площина) зазнає розтягу, а нижня – стиску(рис.6.1.8 В,С). Наявність середнього шару в тілі практично не впливає на опір тіла. Тому деталі машин і механізмів, які зазнають при роботі деформацій прогину, роблять порожнистими, у вигляді труб. Природа теж «подбала» про конструкцію кісток живих організмів, роблячи їх всередині порожнистими.

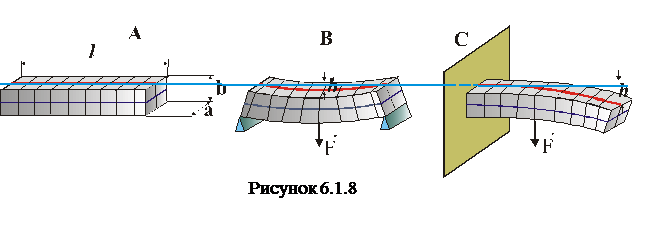При деформації прогину має місце сукупність деформацій розтягу, стиснення, зсуву та кручення, які визначаються модулем Юнга. Отже, у кінцевий вираз для опису деформації прогину повинен входити модуль Юнга. Відповідні розрахунки у спецкурсі опору матеріалів дають наступні формули для визначення величини , яка називається стрілою прогину, під дією сили , прикладеної до середини тіла (цією силою може бути навіть вага цього тіла).

Кінці бруска (балки) знаходяться на двох опорах (рис.6.1.8 В):

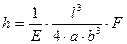. (6.1.9)

Один кінець бруска (балки) закріплений нерухомо (вмурований у стіну) (рис.6.1.8 С):

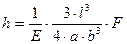(6.1.10)

Як бачимо, деформація прогину визначається модулем Юнга тіла та його геометричними розмірами, причому залежність прогину від геометричних розмірів має особливий характер – залежність у третій степені від довжини та висоти 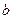тіла. Тому у технічних конструкціях деталі, що зазнають деформацій прогину роблять з

допустимо максимальним значенням

параметру . Наприклад, залізничні рейки, які зазнають великих деформацій прогину, мають особливу форму (рис.6.1.9). Навіть у домашніх умовах можна переконатись у справедливості формули 6.1.9, де прогин обернено пропорційний . Візьміть звичайний листок паперу, покладіть його між двома книжками і зверху поставте склянку води (рис.6.1.10А). Деформація прогину не потребує коментарів. А тепер цей самий папір зігнемо у вигляді «гармошки». Якщо товщина паперу 0,2 мм, а зігнутий у «гармошку» папір – це трикутник приблизно з висотою 20 мм, то, тим самим, стріла прогину під дією того ж навантаження (склянки води) зменшиться у 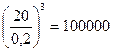раз і такий зігнутий папір без помітної деформації витримує ту ж склянку води (рис6.1.10В).

Деформації прогину мають місце в глобальних масштабах Землі як прогини земної кори. У менших геологічних масштабах деформації прогину можна спостерігати на відкритих поверхнях гір у вигляді синкліналів та антикліналів. Синкліналь (від грецького sinklino – нахиляю) – увігнута складка, вигляд якої показано на рис.6.1.11. Випукла складка (рис.6.1.12) називається антиссинкліналлю.

5. Деформація стиснення (або розтягу).

Деформація усестороннього стиснення (або розтягу) виникає при рівномірному розподілі стискуючих або розтягуючих сили по всій поверхні тіла. Наприклад, до тіла у вигляді куба до всіх його поверхонь, як показано на рис.6.1.13, прикладено однакові сили. Кількісною характеристикою такого виду деформації є відносна зміна об’єму тіла, як відношення абсолютної зміни об’єму 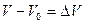до попереднього (початкового) значення об’єму 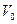. Згідно закону Гука, відносне зменшення або збільшення об’єму ізотропного тіла пропорційне виникаючому у тілі механічному напруженню :

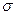, (6.1.11)

де 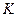– модуль пружності даного тіла, який чисельно дорівнює такому механічному напруженні, при якому відносна зміна об’єму тіла дорівнювала би одиниці, якщо б виконувався лінійний закон деформації Гука.

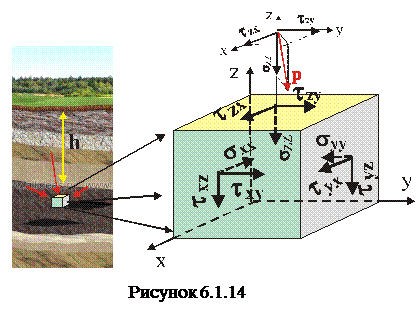Для опису деформацій стиснення або розтягу при нерівномірному розподілі прикладених до тіла сил використовуються елементи тензорного числення. Про поняття тензору інерції йшла мова у розділі «Динаміка обертального руху твердого тіла», де розглядався тензор моменту інерції. А тепер на прикладі деформації гірської породи введемо поняття тензору механічного напруження. Наприклад на глибині знаходиться нафтовий пласт (рис.6.1.14), який зазнає нерівномірного механічного напруження, викликане породами різної густини та товщини над цим пластом. Виділимо елемент такого пласта у вигляді куба, де на рис.6.1.14 червоними стрілками вказані напрями механічний напружень. Розкладемо ці механічні напруження на окремі компоненти, які відносяться до протилежних граней куба по відповідним осям координат. Так, на верхню (жовту) грань куба з координатою 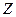механічне напруження Р « тисне вниз» з нормальним напруженням 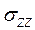і «хоче зсунути» цю грань у напрямі осі ОХ тангенціальними (дотичним) напруженням 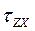та у напрямі осі OY тангенціальним напруженням 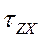. Аналогічно можна визначити напруження, що діють на інші грані виділеного елементу. Таким чином, механічне напруження у виділеному елементі буде визначатись сукупністю з дев’яти напружень – три нормальні напруження та шість тангенціальних напружень. Сукупність цих напружень, які записуються у вигляді матриці, називається тензором напружень:

. (6.1.11)

Компоненти тензора механічних напружень 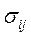дорівнюють відношенню компонента сили 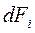, що діє перпендикулярно на елементарну площадку 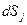до її площі . Таким чином, сила, яка діє на деякий об’єм дорівнює інтегралу тензора напружень на межі цього об’єму по його поверхні . (6.1.12)

6.2 Твердість тіл

1. Твердість – властивість матеріалу протидіяти проникненню у нього іншого, твердішого тіла. Найтвердішим із існуючих сьогодні матеріалів є ультратвердий фулерит (приблизно в 1,17-1,52 разів твердіший за алмаз). Однак це матеріал доступний лише у мікроскопічних кількостях. Тому за взірець найтвердішого матеріалу поки що приймають алмаз і твердість інших матеріалів порівнюють з твердістю алмазу. Але слід зауважити, що в 2010 році російським фізикам Константину Новосьолову та Андре Гейму була вручена Нобелівська премія за відкриття нового унікального матеріалу, названого графеном, на основі вуглецю. Крім того, що цей матеріал володіє різними унікальними електричними та оптичними властивостями, він по міцності на розрив перевищує сталь в 200 разів. Але поки що для порівняння твердості, особливо в мінералогії, використовують шкалу Мосса, названої в честь німецького мінералога Фрідріха Мосса, яку він запропонував в 1811 р. і цей метод і сьогодні широко використовується у мінералогічній практиці. Згідно шкали Мосса мінерали розділяються на 10 класів твердості, де наступний мінерал порівнюється з попереднім по його механічній дії на цей попередній мінерал: залишає подряпини, ріже або піддається обробці.

2. Експериментальні методи визначення твердості матеріалів. Визначення твердості матеріалів за шкалою Мосса дає лише якісну порівняльну характеристику твердості досліджуваного матеріалу. Тому необхідна об’єктивна кількісна характеристика твердості. Існують різні методи експериментального визначення твердості матеріалів. Найбільш поширений метод – це метод Брінелля. Цей метод запропонував шведський інженер Йохан Брінелль в 1900 році і такий метод залишається найбільш поширеним і в даний час. Згідно методу Брінелля, твердість визначається за діаметром відбитка, який залишає стальна загартована металева кулька діаметром 10, 5 або 2,5 мм, що втискується у поверхню досліджуваного матеріалу. Твердість обчислюється як відношення зусилля, прикладеного до кульки, до площі відбитка (причому площа відбитка береться як площа частини сфери, а не як площа кола). Твердість, визначена за цим методом, позначається HB, (H – hardness, англ.– твердість, B – найменування шкали –Brinell)

На рис.6.1.15 наведено принципову схему визначення твердості матеріалів методом Брінелля. За допомогою гідравлічного пресу стальна кулька діаметром D протягом 30 с втискується у досліджуваний матеріал. Після цього визначається діаметр d відбитку і за формулою 6.1.13 розраховується твердість досліджуваного матеріалу в HB.

(6.1.13)

Крім методу Брінелля існують інші методи визначення твердості матеріалів.

Метод Роквелла – твердість визначається за глибиною відбитка металевої кульки чи алмазного конуса у поверхні тестованого матеріалу. Твердість, визначена за цим методом, є безрозмірною і позначається HR.

Метод Віккерса – твердість визначається за величиною відбитка, залишеного чотирикутною алмазною пірамідкою, яка втискується у поверхню. Твердість, визначена за цим методом, позначається HV.

Метод Шора – твердість визначається за висотою відскакування сталевої кульки від поверхні металу, що досліджується, чи за глибиною занурення алмазної голки під дією пружини. Твердість, визначена за цим методом, позначається HSD.

Метод Кузнєцова — Герберта — Ребіндера — твердість визначається часом загасання коливань маятника, опорою якого є досліджуваний метал.

Література

1.Савельев И. В. Курс физики. Том первый. Механика. Молекулярная физика ∕ И. В.Савельев.-М.: Наука. Гл. ред. физ. -мат. лит., 1989. —352 с.

2.Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике, 8-е изд.∕ Б.М.Яворский, А.А.Детлаф, А.К.Лебедев.-М.: Мир, 2006.-1056с

3. Детлаф А.А., Б.М. Яворский Б.М..Курс физики∕ А.А. Детлаф, Б.М. Яворский М.-.Высшая школа.2002.-719с.

4.Трофимова Т.И.,Павловова З.Г.Сборник задач по физике с решениями ∕ Т.И Трофимова, З.Г. Павловова.-М.: Высшая школа, 2001.-405с,

5.Трофимова Т.И. Курс физики. ∕ Т.И. Трохимова.-М.:Высшая школа, 2002Ю-420с.

6.Куліш В. В. Фізика для інженерних спеціальностей.: навчальний посібник для студентів вищих навчальних закладів / В. В. Куліш, Соловйов А.М., Соловйов А.М., Соловйов А.М. - К.: Наука, 2004. - 456 с.

7.Чолпан П.П. Фізика.: підручник для студентів природничих факультетів університетів і педагогічних інститутів / П. П. Чолпан. - К.: Вища школа, 2004. - 567 с. –

8.Загальний курс фізики у трьох томах. Том 1. Механіка.Молекулярна фізика і термодинаміка.Навчальний посібник. Друге видання, виправлене. За ред. Кучерика І.М.-К.-Техніка 2007.-532с

9.Галущак М.О.,Рувімський Б.М. Фізика для інженерів.Навч.посібник∕ М.О.Галущак,Б.М.Рувімський.-Іваоно-Франківськ.:Факел,2006.-216 с.

10.Біленко І.ІФізичний словник ∕ І.І.Біленко.-К.:Вища школа,1993.-319с.

МВ 02070855- 2967 -2010

Федоров О.Є. Фізика. Конспект лекцій.- Івано-Франківськ: ІФНТУНГ, 2010.-210 с.

Даний конспект лекцій узагальнює багаторічний досвід викладання курсу фізики для студентів напряму підготовки 6.040103 – «Геологія». Залишаючи цілісність курсу фізики як фундаментальної дисципліни, у пропонованому конспекті значна увага звертається на професійну орієнтацію курсу фізики. Вже з перших сторінок можна переконатись у такому підході до подання фактичного матеріалу. Значне місце у професійній орієнтації курсу фізики займають питання гравітації, з якими геологи та геофізики мають справу у гравітаційних методах розвідки корисних копалин. На основі фундаментальних фізичних законів розглядається принцип дії сучасної геологічної та геофізичної апаратури. Розглядаючи закони збереження енергії, вказується на проблеми альтернативних джерел енергії.

Цей конспект буде цікавим і зрозумілим навіть для тих, хто не має достатніх математичних знань, оскільки він містить доступні пояснення та ілюстрації.

Зав.кафедри загальної та

прикладної фізики

доктор фіз.-мат.наук, професор М.О. Галущак

Голова навчально-методичного

об’єднання спеціальності,

зав. кафедри

доктор фіз.-мат.наук, професор Петровський

Голова експертно-рецензійної

комісії університету,

зав.кафедри хімії, кандидат хім.наук,

доцент П.Д. Романко

Рецензент

Кандидат фіз.-мат.наук, доцент

кафедри загальної і прикладної фізики М.П. Мазур

Нормоконтролер Г.Я. Онуфрик

Інженер першої категорії Н.В. Мирка

Рекомендовано методичною радою університету (протокол № від………)

© Федоров О.Є.,2010

© ІФНТУНГ, 2010

Дата добавления: 2014-01-07