Критерий Вальда

Матриця виграшів – матриця строками якої є стратегії першого гравця в грі з двома учасниками, стовпцями — стратегії другого гравця, а елемент на перетині строки і стовпця — виграш гравця в ситуації, утвореній відповідними стратегіями. При описанні матричної гри вказується лише матриця виграшів першого гравця. Якщо гру задано платіжною матрицею, в якій вказано величини програшів гравця А, то платіжна матриця гри в цьому випадку називається матрицею програшів.

Зведення гри до матричної форми саме по собі може бути тяж­ким і навіть невиконуваним завданням через незнання стратегій, величезну їх кількість, а також складність оцінки виграшу. Ці при­клади саме й показують обмежені можливості даної теорії, тому що у всіх подібних випадках задача не може бути розв'язана методами теорії ігор.

Таблиця

Загальний вигляд платіжної матриці

В А	В1	В2	…	Вn
А1	а11	а12	...	а1n
А2	а21	а22	...	а2n
. . .	. . .	. . .	. . .	. . .
Am	аm1	аm2	...	аmn

Скінченна парна гра з нульовою сумою називається також ма­тричною грою, оскільки їй можна поставити у відповідність матрицю.

Спочатку звернемо увагу на такий факт. Виходячи з вигляду платіжної матриці, можна зробити висновок, які стратегії є свідомо невигідними. Це ті стратегії, для яких кожен з елементів відповідно­го рядка матриці менший або дорівнює відповідним елементам іншого якого-небудь рядка. Справді, кожен елемент матриці — це виграш гравця А, і якщо для якої-небудь стратегії (рядка) всі виг­раші менші від виграшів іншої стратегії, зрозуміло, що перша стра­тегії менш вигідна, ніж друга. Така операція відбраковування явно невигідних стратегій називається мажоруванням.

Якщо задача зведена до матричної форми, то можна порушу­вати питання про пошук оптимальних стратегій. Насамперед вве­демо поняття верхньої і нижньої ціни гри.

Нижньою ціною гри називається елемент матриці, для якого виконується умова:

α = max min a_ij

i j

Нижня ціна гри показує, що хоч би яку стратегію застосову­вав гравець В, гравець А гарантує собі виграш, не менший за α.

Верхньою ціною гри називається елемент, що задовольняє умову:

β = min max a_ij

i j

Верхня ціна гри гарантує для гравця В, що гравець А не одер­жить виграш, більший за β.

Точка (елемент) матриці, для якої виконується умова:

α = β,

називається сідловою точкою. У сідловій точці найбільший з міні­мальних виграшів гравця А точно дорівнює найменшому з макси­мальних програшів гравця В, тобто мінімум у якому-небудь рядку матриці збігається з максимумом у якому-небудь стовпці.

Формалізація процесу розрахунку ризику за допомогою теорії ігор сприяє поліпшенню розуміння підприємцем проблем у цілому. Таким чином, теорія ігор — власне наука про ризик. Теорія ігор допомагає вирішувати багато економічних проблем, пов'язаних з вибором, визначенням найкращого становища, підпорядкованого тільки тим обмеженням, що випливають з умов самої проблеми.

Дополнительно

В некоторых задачах для состояний природы может быть задано распределение вероятностей, в других — оно неизвестно. Такие игры называют статистическими. Создателем теории статистических игр считается А. Вальд. Он показал, что в теории принятия решении статистические игры являются основным подходом, если решение принимается в условиях частичной неопределенности. Она существенно отличается от антагонистической игры двух лиц с нулевой суммой, где выигрыш одного равен проигрышу другого.

В статистической игре природа не является разумным игроком, который стремится выбрать для себя оптимальные стратегии. Этот игрок не заинтересован в выигрыше. Другое дело — человек, в данном случае статистик. Он имеет целью выиграть игру с воображаемым противником, т. е. с природой.

Игрок-природа не выбирает оптимальной стратегии, но статистик должен стремиться к определению распределения вероятностей состояния природы для того, чтобы выбрать наименее рискованное решение.

4.2. КРИТЕРІЇ ПРИЙНЯТТЯ РІШЕНЬ В УМОВАХ НЕВИЗНАЧЕНОСТІ Дополнительно

Итак, если вопрос распределения вероятностей состояний природы не решен, то используют классические критерии принятия решений в условиях неопределенности.

Один из них - критерий Вальда. критерий крайнего пессимизма. Он аналогичен подходу, применяемому в стратегических играх, где противник крайне агрессивен. Критерий ориентирует лицо, принимающее решение на слишком осторожную линию поведения, поэтому им пользуются в случаях, когда необходимо обеспечить успех при любых возможных условиях.

Важно обратить внимание на исходные условия, так как возможны два подхода - когда решение принимается исходя из матрицы выигрышей (например, прибылей) или исходя из матрицы проигрышей.

Согласно критерию Вальда, если рассматривается матрица выигрышей игрока А, то наилучшим решением будет то, для которого выигрыш окажется максимальным из всех минимальных, при различных вариантах условий. Этот принцип называется критерием максимина.

Формализованное выражение максимина выглядит так:

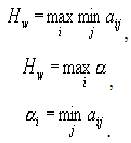
Максиминний критерий Вальда совпадает с критерием выбора стратегии позволяющим получить нижнюю цену игры для двух лиц с нулевой суммой. Согласно этому критерию выбирается стратегия, гарантирующая при любых условиях выигрыши, не меньшие чем

.

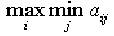Иными словами, максиминний критерий Валъда используется в случаях, когда требуется гарантия, чтобы выигрыш в любых условиях оказался не менее, чем наибольший из возможных в худших условиях (лучший из худших).

Если рассматривается матрица проигрышей игрока А, то наилучшим решением согласно критерию Вальда будет то, для которого выигрыш окажется минимальным из всех максимальных, при различных вариантах условий. Этот принцип называется критерием минимакса.

Формализованное выражение минимакса выглядит так:

Иными словами, минимаксный критерий Вальда используется в случаях, когда требуется гарантия, чтобы проигрыш в любых условиях оказался не больше, чем наименьший из возможных в худших условиях (лучший из худших).

Данный критерий прост и четок, но консервативен в том смысле, что ориентирует принимающего решение на слишком осторожную линию поведения. Поэтому критерием Вальда, главным образом, пользуются в случаях, когда необходимо обеспечить успех прилюбых возможных условиях.

Дата добавления: 2014-01-07