Общее условие устойчивости дискретных систем

АНАЛИЗ УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ

Устойчивость системы характеризуется ее свободным движением, которое определяется свободной составляющей процесса регулирования выходной величины. Линейная дискретная система называется устойчивой, если свободная составляющая процесса регулирования 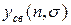затухает с течением времени. Сформулированное условие устойчивости сводится к выполнению равенства:

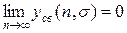(24.1)

для всех 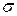из интервала 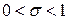. Если хотя бы для одного значения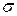

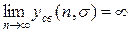(24.2)

то дискретная система называется неустойчивой. Если, наконец,

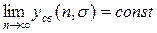(24.3)

или не существует, то дискретная система находится на границе устойчивости.

В подавляющем большинстве случаев величина предела 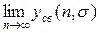при любом 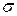определяется его значением при 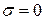. В тех случаях, когда при 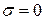выполняется соотношение (24.1), а при 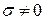- любое из соотношений (24.2), (24.3) говорят о так называемой высокочастотной неустойчивости дискретной системы.

Таким образом, чтобы оценить устойчивость дискретной системы, необходимо найти свободную составляющую процесса регулирования. Свободная составляющая процесса управления определяется решением однородного разностного уравнения замкнутой дискретной системы

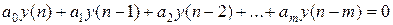, (24.4)

где m - порядок системы.

Решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

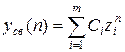(24.5)

где 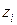- корни характеристического уравнения

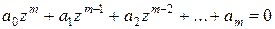(24.6)

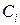- постоянные коэффициенты, значения которых зависят от свойств системы, характера внешнего воздействия и относительного времени .

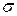Из решения (24.5) следует, что для устойчивости дискретной системы необходимо и достаточно, чтобы все корни характеристического уравнения замкнутой системы (полюса передаточной функции замкнутой дискретной системы 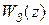) удовлетворяли условию

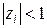; i = 1, 2, 3,…, m. (24.7)

Если хотя бы один корень 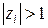, система будет неустойчивой. Значением какого-либо корня 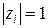при всех остальных 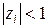определяется граница устойчивости дискретной системы.

Для устойчивости дискретной системы необходимо и достаточно, чтобы все корни характеристического уравнения замкнутой системы находились внутри круга единичного радиуса с центром в начале координат.

Графически область устойчивости дискретной системы на плоскости 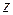корней характеристического уравнения изображается единичным кругом.

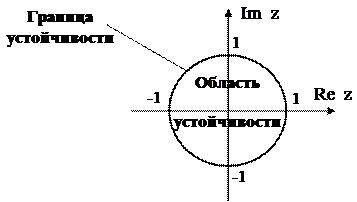Рисунок 24.1. Области устойчивости на плоскости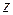

Таким образом, исследование устойчивости сводится к изучению расположения корней характеристического уравнения замкнутой дискретной системы относительно единичной окружности.

Для суждения об устойчивости дискретных систем можно использовать обычные критерии устойчивости линейных систем, но при этом приходится учитывать лишь некоторые особенности дискретных систем.

Дата добавления: 2014-01-07