Лекція №1. Поняття інтеграла разом із поняттям похідної і диференціала є фундаментальним поняттям вищої математики

Вступ

Поняття інтеграла разом із поняттям похідної і диференціала є фундаментальним поняттям вищої математики.

Необхідність в інтегральному численні викликають задачі практичної напрямленості, а саме: необхідність обчислення маси неоднорідного тіла, площ фігур досить складного характеру, роботи змінних сил, об’єми тіл, центрів тяжіння, тощо, а також необхідність визначити функцію, якщо відома її похідна. Всі ці задачі привели до розвитку інтегрального числення.

Порівняємо задачі диференціального та інтегрального числень.

Задача диференціального числення. Знайти похідну або диференціал заданої функції .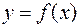

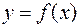Задача інтегрального числення. За заданою функцією знайти функцію таку, щоб або .

Очевидно, що задача інтегрального числення є оберненою до задачі диференціального числення і полягає в тому, щоб відновити функцію по заданій її похідній. Ця задача приводить до поняття первісної функції та невизначеного інтеграла.

Основні поняття і початки інтегрального числення були розроблені в кінці 17ст. Ісааком Ньютоном (1643-1727) і Готфридом Лейбніцем (1646-1716). Термін “інтеграл” ввів Якоб Бернуллі (1654-1705) у 1690р.

1. Поняття первісної та невизначеного інтеграла

Означення. Функція називається первісною функції на проміжку , якщо диференційована на і або, що те ж саме, .

Теорема. Якщо – первісна функції на проміжку , то всяка інша первісна функції на цьому ж проміжку відрізняється від на сталу величину, тобто має вигляд .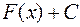

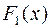Доведення. Нехайі - первісні функції на . За означенням первісної і .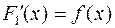

Розглянемо функцію . Для всіх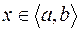

За необхідною і достатньою умовою сталості функції на проміжку маємо 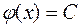. Отже .à

З теореми випливає, що всі первісні даної функції є елементами множини , де - одна з первісних функцій , а - довільна стала.

Означення. Вираз 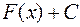, де функція – первісна функції на , - довільна стала, називається невизначеним інтегралом функції на і позначається .

За означенням,

якщо, то .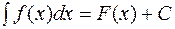

Знак називається інтегралом,

- підінтегральним виразом,

- підінтегральною функцією,

- змінною інтегрування.

З означення випливає що невизначений інтеграл є сукупність первісних функцій .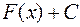

Геометрично невизначений інтеграл є множина кривих, кожна з яких називається інтегральною кривою. Ця множина утворюється зсувом однієї з інтегральних кривих паралельно самій собі вздовж осі :

Теорема (про існування невизначеного інтеграла). Якщо функція неперервна на прміжку , то вона має на цьому проміжку первісну (невизначений інтеграл).

Визначення. Задача знаходження невизначеного інтеграла від функції називається її інтегруванням.

2. Властивості невизначеного інтеграла

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції

.

Доведення. Дійсно, .

Операції диференціювання і інтегрування є взаємно обернені, тому правильність виконання операції інтегрування перевірюється диференціюванням.

2. Диференціал від невизначеного інтеграла дорівнює підінтегральній функції:

.

Доведення. Дійсно, .

3. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:

.

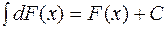Доведення. Дійсно, .

4. Сталий множник можна виносити за знак інтеграла:

.

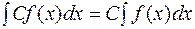5. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі інтегралів від цих функцій:

.

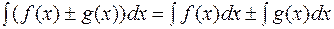Зауваження. Властивості 4 і 5 називаються лінійними властивостями інтеграла.

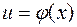6. (Інваріантність формули інтегрування). Якщо і - довільна функція що має неперервну похідну, то .

Доведення. Нехай - незалежна змінна. Тоді . Проінтегруємо обидві частини: .

Нехай тепер 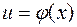- функція незалежної змінної . Тоді згідно з властивістю інваріантності форми першого диференціала

.

Проінтегруємо обидві частини

.

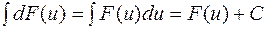Таким чином, будь-яка формула інтегрування зберігає свій вигляд незалежно від того, чи змінна інтегрування є незалежною змінною, чи довільною функцією від незалежної змінної, яка має неперервну похідну.à

З властивості 6 випливає, що загальний вигляд формули інтегрування є

.

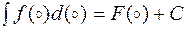3. Таблиця основних інтегралів

Якщо 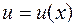- довільна функція, що має на деякому проміжку неперервну похідну 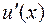, то на цьому проміжку мають місце формули

1. ;

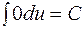2. ;

3. , ; ;

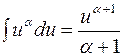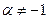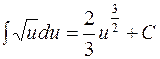4. ; ; ;

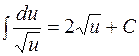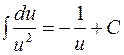5. ;

6. ; ;

7. ; ;

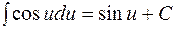8. ; ;

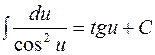9. ; ;

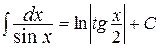10. ; ;

11. ; ;

12. ; ;

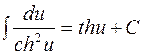13. ; ;

14. ;

15. ;

16. ;

17. ;

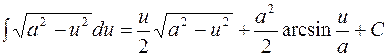18. ;

19. ;

20. .

Перевірити таблицю інтегралів можна за означенням первісної шляхом диференціювання правих частин.

Таблиця і властивості дозволяють знайти інтеграли інших функцій. Інтеграли, які містяться в таблиці будемо називати табличними.

4. Основні методи інтегрування

1. Метод безпосереднього інтегрування.

Безпосереднє інтегрування – це обчислення інтегралів за допомогою основних властивостей невизначеного інтеграла і таблиці. При цьому часто використовується розклад підінтегральної функції у суму декількох функцій, інтеграли від яких є табличними.

Зауваження. При кожному інтегруванні утворюються проміжні довільні сталі, але у відповідь записують лише одну загальну сталу, яка є сумою всіх проміжних сталих.

2. Метод заміни змінної (підстановки).

Цей метод ґрунтується на теоремі.

Теорема. (про заміну змінної у невизначеному інтегралі). Якщо функція 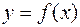неперервна на проміжку , а функція 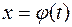визначена, набуває значень, диференційована на проміжку і має на обернену функцію , то справедлива формула:

. (1)

Доведення. Продиференціюємо обидві частини даної рівності по .

(ліва частиназа властивістю 1.

(права частина(за правилом диференціювання складеної функції і диференціювання оберненої функції).

Таким чином, ліва частина дорівнює правій частині.à

Доведена теорема застосовується двома способами:

1 спосіб. Введення функції під знак диференціала

1) Інтеграл 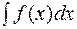записують у вигляді

,

де для функції відома первісна ,

2) За формулою (1)

. (2)

На практиці розв’язування цим способом оформлюють у вигляді:

2 спосіб. Виведення функції з-під знаку диференціала

1) Інтеграл 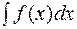записують у вигляді

,

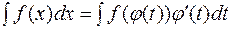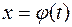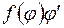де функція має обернену функцію і для функції відома первісна.

2) За формулою (1)

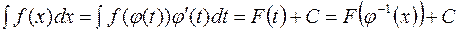. (3)

На практиці розв’язування цим способом оформлюють у вигляді:

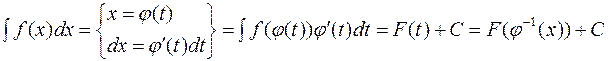
Таким чином, при інтегруванні заміною змінної виконуються підстановки двох видів: і 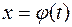. Ці підстановки підбираються так, щоб одержані нові інтеграли у формулах (2) і (3) були б табличними. Загальних методів підбору підстановок не існує, вміння правильно визначати підстановку набувається практикою.

3. Метод інтегрування частинами.

Теорема. Якщо дві функції і неперервні і диференційовані на проміжку , то на цьому проміжку має місце формула:

.

Доведення. Продиференціюємо обидві частини формули по :

Права частина за властивістю 1; ліва частина

Ліва частина відрізняється від правої на довільну сталу:

;

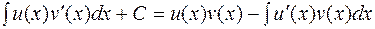отже

.à

Доведена формула називається формулою інтегрування частинами і застосовується на практиці у стислому вигляді

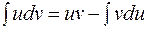(4)

Зауваження. Для деяких студентів формула (4) визиває труднощі, тому, використовуючи заміну , , 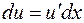можна її переписати у вигляді

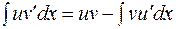(5)

Під час інтегрування частинами треба подати підінтегральну функцію у вигляді так, щоб інтеграл в правій частині формули був в обчислювальному відношенні простішим, ніж інтеграл в лівій частині. В цьому допоможуть правила:

1. Інтеграли вигляду ; ; 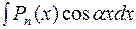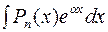обчислюються частинами, причому за 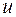береться многочлен , за - вираз, що лишився. Це приводити до зниження степеня многочлена . Якщо степінь многочлена більше 1, то інтегрування частинами застосовується багаторазово.

2. Інтеграли вигляду ; ; ; 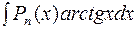обчислюються частинами, причому за 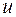беремо 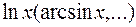, а за .

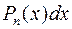3. При обчисленні інтегралів вигляду 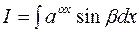, , 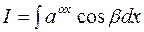депісля двократного застосування формули інтегрування частинами утворюється лінійне рівняння відносно шуканого інтеграла , який знаходять, розв’язуючи це рівняння.

Дата добавления: 2014-01-07