Характеристики центру розподілу

Графічне щображення рядів розподілу.

Для чіткого уявлення про характер розподілу застосовують графічне зображення рядів розподілу. Основними способами графічного зображення рядів розподілу є полігон, гістограма, огіва,, кумулята і крива Лоренца.

Полігон розподілу будується в прямокутній системі координат, при цьому на осі абсцис відкладається варіанта, а на осі ординат - частота або частість. За допомогою полігону розподілу графічно зображують, як правило, дискретні варіаційні ряди.

Гістограму застосовують для зображення інтервальних варіаційних рядів. При її побудові на осі абсцис відкладають відрізки, які зображують інтервал. Висота кожного стовпчика повина бути пропорційною частотам.

Для зображення варіаційного ряду з нагромадженими частотами у прямокутній системі координат застосовують кумуляту і огіву.

Кумулята - будується в прямокутній системі координат, при цьому на осі абсцисс відкладають значення варіант, а на осі ординат - нагромаджені частоти.

Аналогічно кумуляті в прямокутній системі координат будують огіву. Різниця графіка лише в тому, що на вісь абсцисс відкладають нагромаджені частоти, а на вісь ординат - значення варіант.

Характеристиками центру розподілу, крім середньої арифметичної, є мода та медіана. Ці характеристики називають структурними середніми і розглядають з такими, як квартилі та децилі.

Мода - це варіанта, яка найчастіше повторюється у варіаційному ряду розподілу. В дискретних варіаційних рядах моду легко визначити візуально. В інтервальних варіаційних рядах модальне значення наближено обчислюють за формулою:

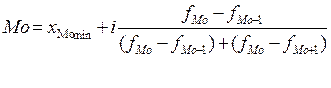
де 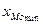- нижня межа модального інтервалу. Модальним є інтервал, якому відповідає найбільша частота;

і – крок інтервалу;

- частота модального інтервалу;

- частота інтервалу, що передує модальному;

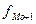- частота інтервалу, що слідує за модальним.

Медіана - це варіанта, що ділить ранжирований ряд на дві рівні за обсягом частини. Якщо кількість членів ряду парна, то медіана дорівнює середній арифметичній із двох серединних значень варіант. Для обчислення медіани в інтервальному варіаційному ряду розподілу застосовують формулу:

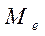
де - нижня межа медіального інтервалу;

і - крок інтервалу;

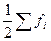- півсума нагромаджених частот інтервального ряду;

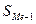- сума нагромаджених частот перед медіальним інтервалом;

- частота медіального інтервалу.

Для аналізу закономірностей розподілу використовують такі характеристики як квартилі та децилі.

Квартилі – це варіанти, які діляють упорядкований ряд на чотири рівні частини. Перша квартиль Qвідокремлює 25% одиниць сукупності:

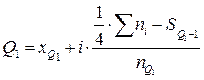
Друга квартиль дорівнює медіані.

Третя квартиль відокремлює 75% одиниць сукупності:

Децилі – це варіанти, які ділять упорядкований ряд на десять рівних частин. Всього може бути дев’ять децилів.

Дата добавления: 2014-01-07