Інтерполяція функцій однієї й двох змінних

Крім функцій, заданих аналітично (тобто за допомогою елементарних функцій, значення яких легко можуть бути обчислені в будь-якій крапці області визначення), на практиці часто доводиться мати справа з таблично заданими функціями. У цьому випадку функція задається своїми значеннями на деякій дискретній безлічі крапок (вузлів) з області визначення. Якщо необхідно одержати значення функції в якій-небудь крапці, що не збігається з вузлом, використовують різні методи наближеного обчислення, які ґрунтуються на деяких апріорних припущеннях щодо цієї функції. При цьому сама процедура обчислення називається інтерполяцією у випадку, коли крапка належить заданій області, і екстраполяцією, якщо вона лежить поза областю.

Як припущення про характер дискретно заданої функції найбільше часто використовуваної й простій є те, що вона кусково- лінійна, тобто що в проміжках між вузлами вона поводиться відповідно до лінійного закону. Тоді інтерполяція називається лінійної, і цей метод ми будемо досить часто застосовувати в алгоритмах комп'ютерної графіки.

Нехай на площині задана система координат і відрізок на осі 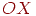, на кінцях якого задані значення деякої лінійної функції (мал. 4.3). Тоді для будь-якої крапки 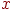усередині заданого відрізка відповідне значення обчислюється по формулах

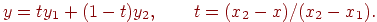
Рис. 4.3. Лінійна інтерполяція функції однієї змінної

Звернемося тепер до завдання інтерполяції функцій двох змінних. У цьому випадку найбільш простої також є інтерполяція по трьох заданих крапках знову ж за допомогою кусочно-лінійної функції. Нехай на площині заданий трикутник з вершинами 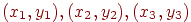й задані значення функції в цих крапках . Тоді три крапки визначають у просторі трикутник, що є плоскою фігурою. Передбачається, що площа трикутника більше нуля, або, як говорять, трикутник невырождений. Для визначення значення функції в довільній крапці 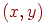, що лежить усередині трикутника, скористаємося так званими барицентричними координатами цієї крапки. Геометричний зміст цих координат полягає в тім, що вони дорівнюють відношенню площ трикутників, зображених на мал. 4.4:

Рис. 4.4. Лінійна інтерполяція функції двох змінних

Ці числа ненегативні й задовольняють наступним співвідношенням:

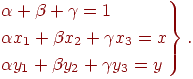
Ці співвідношення будемо розглядати як рівняння для знаходження чисел .

Визначник цієї системи рівнянь є

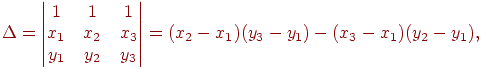
і він по модулі дорівнює подвоєної площі трикутника, тому , отже, система має єдине рішення при будь-якій правій частині. Скористаємося формулами Крамера й випишемо вид цього рішення:

де

Після того як отримані барицентричними координати крапки 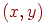, значення функції в ній розраховується по формулі

Існують добре розроблені методи гладкої інтерполяції функцій. Особливо часто при інтерполяції кривих і поверхонь використовуються сплайн- функції, які гладко "склеюються" з поліномів. Серед них варто виділити кубічні сплайни, які будуються з поліномів третього ступеня. Вони широко використовуються в інженерній геометрії завдяки простоті їхнього обчислення й інших корисних властивостей. Ми їх розглянемо докладніше в наступних главах.

Дата добавления: 2014-01-07