
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Чебишева. Закон великих чисел - це є цілий ряд теорем, які встановлюють умови збіжності середнього арифметичного випадкових величин до середніх арифметичних їхніх
|
|
|
|
Закон великих чисел
Закон великих чисел - це є цілий ряд теорем, які встановлюють умови збіжності середнього арифметичного випадкових величин до середніх арифметичних їхніх математичних сподівань.
Розглянемо послідовність випадкових величин 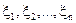 .
.
Послідовність збігається за ймовірностю до деякого числа b при n→ ∞, якщо

Нехай 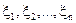 - послідовність незалежних випадкових величин, дисперсії яких обмежені деяким числом c:
- послідовність незалежних випадкових величин, дисперсії яких обмежені деяким числом c:  c, i=1,2..,n Тоді при n → ∞ для будь-якого
c, i=1,2..,n Тоді при n → ∞ для будь-якого 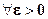
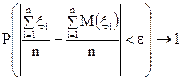
Це твердження можна записати інакше, в еквівалентній формі.
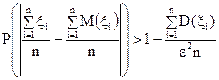 , (35)
, (35)
яку використовують при розв’язанні прикладних завдань.
Зокрема, звідси випливає твердження (теорема Хінчина):
Якщо 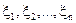 - послідовність попарно незалежних випадкових величин з однаковим математичним сподіванням a і дисперсією σ2, то при n → ∞ для будь-якого
- послідовність попарно незалежних випадкових величин з однаковим математичним сподіванням a і дисперсією σ2, то при n → ∞ для будь-якого 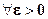
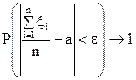 ,
,
або в еквівалентній формі
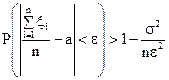 (36)
(36)
Теорема Бернуллі.
Застосуємо теорему Хінчина до випадкової величини 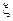 = m – число появ події А в серії n незалежних випробувань. Представимо цю випадкову величину у вигляді суми попарно незалежних, однаково розподілених випадкових величин
= m – число появ події А в серії n незалежних випробувань. Представимо цю випадкову величину у вигляді суми попарно незалежних, однаково розподілених випадкових величин 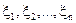 ,
,
xі =  (37)
(37)
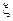 = m=
= m= 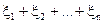
Імовірності р(А) = р, р ( ) = 1 - р = q, М (
) = 1 - р = q, М ( 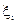 ) = р, D (
) = р, D ( 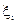 ) = pq. Тоді при
) = pq. Тоді при
n → ∞ і для будь-якого 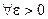
 ,
,
або в еквівалентній формі
 . (38)
. (38)
Зміст цієї теореми полягає в тому, що відносна частота появи події за ймовірностю збігається до ймовірності цієї події.
Узагальненням теореми Бернуллі на випадок, коли випробування відбуваються при неоднакових умовах, що викликає зміну ймовірності появи події А, є теорема Пуассона.
Теорема Пуассона.
Розглянемо послідовність n незалежних випробувань, у кожному з яких подія А наступає з імовірністю р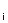 , i=1,2,…n...Міркуючи так само,
, i=1,2,…n...Міркуючи так само,
|
|
|
як і в попередньому випадку, одержимо М ( 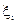 ) = р
) = р 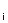 , D (
, D ( 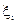 ) = р
) = р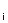 q
q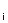 . За теоремою Чебишева одержимо
. За теоремою Чебишева одержимо
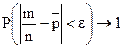 , де
, де 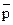 =
= 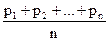 , тобто відносна частота появи події А збігається по ймовірності до середньої арифметичної ймовірностей цієї події в кожному випробуванні.
, тобто відносна частота появи події А збігається по ймовірності до середньої арифметичної ймовірностей цієї події в кожному випробуванні.
Запишемо твердження теореми Пуассона в еквівалентній формі
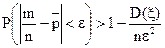 ,
, (39)
(39)
де 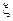 = m =
= m =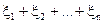 , а
, а 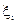 (i=1,2,..n)визначені у (37).
(i=1,2,..n)визначені у (37).
Розглянемо приклад на застосування закону великих чисел.
Приклад 17. з 100 виробів, що відправляють у складальний цех, було піддано обстеженню 200, відібраних випадковим образом. Серед них виявилося 25 бракованих. Прийнявши частку бракованих виробів серед відібраних, за ймовірність виготовлення бракованого виробу, оцінити ймовірність того, щоу всій партії бракованих виробів виявиться в межах від 15% до 20%.
Для розв’язання задачі використаємо нерівність (38). Ймовірність виготовлення бракованого виробу умовно задачі  . Потрібно знайти ймовірність
. Потрібно знайти ймовірність
Р(0,10  0,15). Віднімемо в кожній частині нерівності р=0,125, одержимо
0,15). Віднімемо в кожній частині нерівності р=0,125, одержимо
Р(0,10 – 0,125 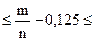 0,15– 0,125) = Р(– 0,025
0,15– 0,125) = Р(– 0,025  0,025) або
0,025) або
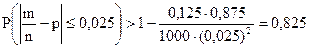 .
.
Перша нерівність Чебишева.
Якщо випадкова величина 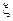 має скінчений перший абсолютний момент
має скінчений перший абсолютний момент
 , то
, то 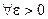
 . (40)
. (40)
Зокрема, якщо  й існує
й існує 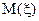 , то
, то
 . (41)
. (41)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 707; Нарушение авторских прав?; Мы поможем в написании вашей работы!