Метод Гауса

Метод Гаусса розв’язування системи т лінійних рівнянь з п невідомими являє собою метод послідовного виключення змінних з рівнянь системи. Розв’язання СЛАР методом Гаусса можна умовно розділити на 2 етапи: прямий та зворотний хід.

Прямий хід методу Гауса саме і полягає в послідовному виключенні змінних (невідомих) з рівнянь системи.

Не порушуючи загальності, будемо вважати, що 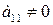, в іншому випадку можна переставити невідомі. Отже, маємо систему:

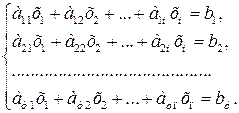
Перший крок: за допомогою першого (робочого) рівняння з усіх наступних рівнянь виключимо х ₁, для чого перше помножимо на 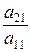і віднімемо від другого, потім – на 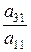і віднімемо від третього і т.д. Одержимо систему, еквівалентну даній:

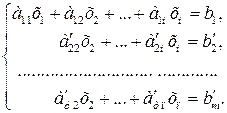
Припустивши, що 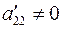, аналогічно виключимо 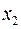з третього і наступних рівнянь (перше рівняння на даному етапі вже виконало свою місію і в подальших перетвореннях участі не бере, а переписується без змін; робочим тепер є друге рівняння).

Продовжуючи процес послідовного виключення невідомих, ми побачимо, що система набуває простішого виду.

Пропускаючи деякі моменти, зауважимо, що зворотний хід методу починається з відшукання (або вираження) певної змінної із останнього рівняння системи, після чого знаходять значення інших змінних (або виразів для них), послідовно повертаючись від останнього до першого рівняння.

Класифікація систем за кількістю розв’язків.

При розв’язуванні системи лінійних алгебраїчних рівнянь методом Гаусса можемо отримати наступні випадки:

· якщо одне з рівнянь набуває вигляду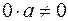, то система несумісна;

· якщо система набуває трикутного виду і кількість рівнянь дорівнює кількості невідомих, то система має єдиний розв'язок (тобто система сумісна і визначена);

· якщо система має менше рівнянь, ніж невідомих, то вона сумісна і невизначена.

Припустимо, що в системі залишилось 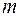рівнянь з 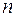невідомими 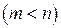. Будь-які 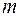змінних (невідомих) системи 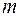лінійних рівнянь з 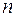змінними (невідомими) 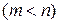називаються основними, якщо визначник із коефіцієнтів при них відмінний від нуля, а інші 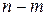– неосновними (або вільними).

Основними можуть бути різні групи із т змінних. Кількість різних способів вибору т змінних із загального їх числа скінченна і дорівнює числу комбінацій із 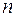елементів по т, тобто 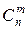. Отже, кількість способів розбиття 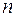змінних системи на основні і неосновні обмежена цим числом.

Із нескінченної множини розв’язків системи 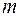лінійних рівнянь з 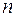невідомими 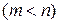виділимо так звані базисні.

Базисним розв'язком системи т лінійних рівнянь з п невідомими називається всякий її розв’язок, в якому неосновні змінні мають нульові значення. Кожному розбиттю змінних системи на основні і неосновні відповідає один базисний розв’язок. Отже, існує не більше ніж 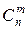базисних розв'язків системи.

Якщо в базисному розв'язку деякі основні невідомі рівні нулеві, то такий базисний розв’язок називається виродженим.

Серед розв’язків системи т лінійних рівнянь з п невідомими, в тому числі і базисних, слід виділити ті, всі компоненти яких невід’ємні.

Базисний розв'язок системи т лінійних рівнянь з п невідомими називається допустимим, якщо всі компоненти його невід’ємні, і недопустимим, якщо хоча б одна компонента від’ємна.

Практично для розв’язування систем лінійних рівнянь спрощують не систему, а розширену матрицю системи:

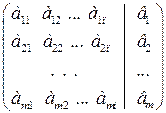
Над матрицею виконують елементарні перетворення: змінюють порядок рядків, множать рядки на відмінне від нуля число, до будь-якого рядка матриці додають інший, помножений на деяке відмінне від нуля число. Внаслідок таких перетворень кожен раз одержують розширену матрицю системи, рівносильну даній.

Приклад. Розв’язати систему: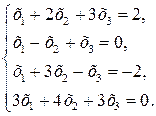

Розв’язання. Прямий хід методу. Записуємо розширену матрицю системи і виконуємо над нею елементарні перетворення:

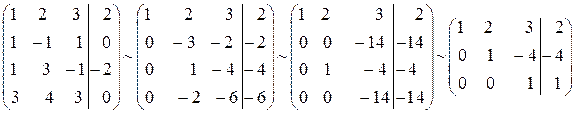
Зворотний хід методу. За останньою матрицею відновлюємо систему рівнянь:

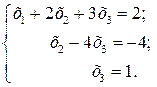
З неї послідовно отримуємо: 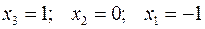. Шуканий розв’язок: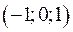

Приклад. Розв’язати систему: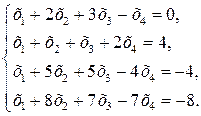

Розв’язання.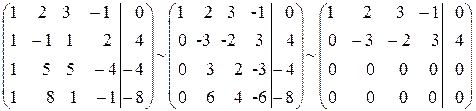

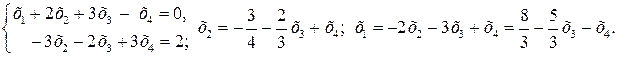
Нехай – основні (базисні) змінні; 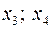– неосновні (вільні).

Загальний розв’язок системи: .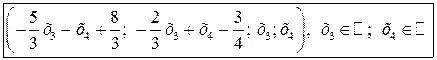

Поклавши 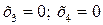, отримаємо базисний розв’язок:

.

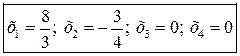Приклад. Розв’язати систему: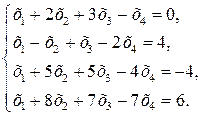

Розв’язання. Прямий хід: .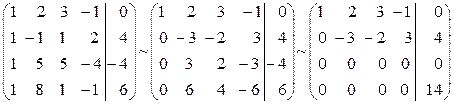

Зворотний хід: 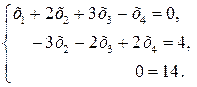Оскільки 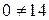, то система несумісна.

Однорідні лінійні рівняння — це рівняння, вільні члени яких рівні нулю.Система однорідних рівнянь завжди сумісна, оскільки має нульовий розв'язок (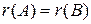, так як 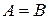). Важливим є питання: при якій умові система має ненульові розв'язки, тобто є невизначеною? Відповідь дають наступні теореми.

Теорема 1. Для того, щоб однорідна система мала ненульові розв'язки, необхідно і достатньо, щоб ранг r її матриці коефіцієнтів був менше п.

Дійсно, якщо 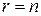, то система має єдиний розв’язок: .

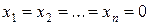Якщо ж 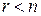, то система невизначена (несумісною вона не буває), отже, має ненульові розв’язки серед множини розв’язків.

Із доведеної теореми випливає:

Теорема 2. Для того, щоб однорідна система п лінійних рівнянь з п невідомими мала ненульові розв’язки, необхідно і достатньо, щоб її визначник дорівнював нулю.

Твердження теореми 2 є частинним випадком теореми Кронекера-Капеллі.

Таким чином, нами розглянуто 3 методи розв’язування систем лінійних рівнянь. На відміну від матричного методу і методу Крамера, метод Гаусса дозволяє розв'язувати системи, в яких кількість рівнянь і кількість невідомих можуть бути різні. Ця суттєва відмінність привела до поширеності цього методу в лінійному програмуванні та при використанні комп’ютерних технологій.

Дата добавления: 2014-01-07