Звездная система координат

СИСТЕМЫ ПРИМЕНЯЕМЫХ В ГЕОДЕЗИИ КООРДИНАТ, СПОСОБЫ ИХ ОПРЕДЕЛЕНИЯ

Установление систем координат и их измерение в избранной системе являются важнейшими задачами геодезии. Эти измерения могут быть абсолютными и относительными, определение может быть прямым или косвенным — посредством передачи координат с соседнего пункта. В настоящее время наибольшее распростране­ние в геодезии получили следующие системы координат: звезд­ная, астрономическая (поверхность относимости — геоид), гео­дезическая (поверхность относимости — эллипсоид), общезем­ная, или геоцентрическая (прямоугольная трехосная система с началом координат в центре масс Земли), государственная пря­моугольная на плоскости (картографическая проекция государ­ственных топографических карт).

Измерение астрономических координат — широты и долготы (ф, X) — основано на определении взаимного углового располо­жения вертикали места (отвесной линии) и направления на ка­кое-либо небесное светило, звездные координаты которого изве­стны. В результате суточного и годового движения Земли взаимное расположение этих линий непрерывно меняется, поэтому наряду с измерением угловых величин обязательным измерениям подле­жит и время.

Положение каждого небесного светила на небесном своде определяется двумя параметрами в звездной системе координат (рис. 5.1) — склонением 8 и прямым восхождением а. Исходными отсчетными кругами являются небесный экватор 1 (эту систему называют иногда экваториальной) и меридиан 2 точки Овна у — точки весеннего равноденствия. Прямое восхождение светила а — дуга, отсчитываемая вдоль экватора к востоку от точки Овна до меридиана светила М, может принимать значения от 0 до 360°. Склонением 8 называют дугу меридиана светила М от небесного экватора 1 до светила. Склонение может быть от 0 до 90° к северу или к югу (например, 39°Л^или 64° 5).

Установлению систем координат небесных светил и их измере­ниям посвящен раздел астрономии — астрометрия, иногда опре­деляемая как наука об измерении времени и пространства. Важ-

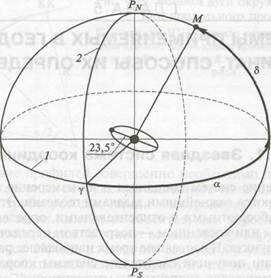
Рис. 5.1. Звездная система координат:

рк — Северный полюс мира; Р.5— Южный полюс мира; М — светило; у — точка Овна; а — прямое восхождение светила М; 8 — склонение светила М; 1 — небес­ный экватор; 2 — меридиан Овна; 23,5° — угол наклона орбиты Земли относи­тельно эклиптики

нейшая задача астрометрии — накопление измерений координат звезд и издание их в виде таблиц — звездных каталогов. С древней­ших времен человек затрачивал огромные усилия на создание этих каталогов, имена их авторов навечно записаны в историю науки: Гиппарх (125 г. до н.э., 1022 звезды, точность координат около 15'), Улугбек (1438 г., 1 017 звезд), Тихо Браге (1602 г., 1 005 звезд, точность 2'). Казалось, что последним наивысшим научным дос­тижением на этом пути станет фундаментальный каталог РК5 (1988 г.), обобщивший результаты 300 частных звездных катало­гов. Однако небольшими частями начинает выходить новый ката­лог РК6, объединяющий данные каталога РК5 и результаты, по­лучаемые с помощью астрометрического спутника Шррагсов. На­мечена замена фундаментальных опорных плоскостей звездных систем координат — плоскостей экватора и эклиптики — систе­мой фиксированных направлений на 212 квазаров, принимаемых за неподвижные. Новую небесную отсчетную систему предложено называть 1СК8 (ШегпаИопа! Се1ез11а1 КеГегепсе 8у81ет).

Каталог РК5 содержит координаты основных 1535 звезд до седь­мой звездной величины (1^т) с точностями: 5_а = 0,001 с, 5₅ = 0,01". Звездная величина — параметр яркости звезды, вычисляется по формуле

т = -2,5\!>Е + с,

где Е — освещенность, -2,5 — шаг шкалы звездных величин; с -постоянная величина, нулытункт шкалы. Для Солнца т = -26,78, доя Луны т = -12,71, самая яркая звезда Сириус имеет звездную величину -1,46, глаз человека различает звезды до 6 — 7™. Самые мощные телескопы путем накопления световой энергии на фото­слое позволяют регистрировать звезды до 23^т.

Во всех развитых странах издаются на несколько лет вперед таблицы координат звезд. В России Институтом теоретической ас­трономии (Санкт-Петербург) издается «Астрономический ежегод­ник» (АЕ), содержащий координаты 695 звезд ярче 4,5^т.

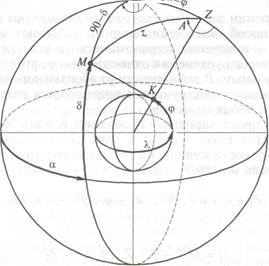
Задачи по определению астрономических координат ср и Я, обыч­но решаются раздельно. Астрономическая широта <р в общем слу­чае может быть найдена из решения параллактического треуголь­ника М2Р (рис. 5.2) по формулам:

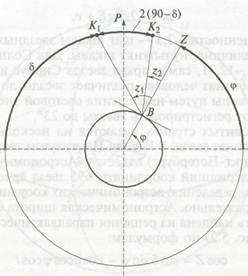
Рис. 5.3. Наблюдение близполюсной звезды в двух кульминациях:

В — точка наблюдения; Р — полюс мира; 2 — точка зенита; К_}, К_г — кульмина­ции Полярной звезды; ср — широта точки наблюдения; 5 — склонение Полярной звезды; гь ф — зенитные расстояния К\ и К₂

При измерении зенитных расстояний применяют первую фор­мулу, этот способ нахождения широты называют зенитальным. Второй путь — измерение астрономического азимута А светила М и решение второго уравнения относительно <р, этот способ назы­вают азимутальным. В зависимости от абсолютного значения ши­роты и имеющихся инструментов применяются различные част­ные варианты обоих способов.

Наиболее прост вариант наблюдений близполюсной звезды (например, Полярной звезды) в двух кульминациях (К^ и К₂, рис. 5.3) в плоскости меридиана точки наблюдения В, когда часо­вой угол ( равен 0 и 180°:

2! + ф + 8 = 180°; 2₂ + ф + 90° - 8 = 90°. Откуда

Ф = 180° - 8 - 21, Ф = 8 - 22.

Складывая почленно, получим

2ф = 180° - 2₁ - 2ъ

Ф = 90° - (2₁ +

Дата добавления: 2014-01-06