Переміщення, шлях, вектори швидкості і прискорення

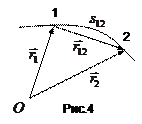Переміщенням, або вектором переміщення, називається вектор, початок якого співпадає з початковим положенням частинки, а кінець – з кінцевим положенням. Із рис.4 видно, що вектор переміщення точки 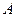є приріст радіуса-вектора 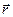за час : . Вказані на рис.4 вектори 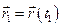і , визначають положення частинки, відповідно, початковий 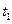і кінцевий моменти часу в процесі руху. Інтервалу часу 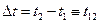відповідає вектор переміщення частинки .

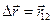Іншою характеристикою є шлях матеріальної точки.

Шляхом називається довжина дуги траєкторії, яка зв’язує початкове і кінцеве положення точки. Для порівняння на рис.5 показані шлях (довжина кривої) і переміщення (пряма).

Введемо поняття швидкості точки. Відношення 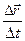називають середнім вектором швидкості 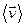за час .

.

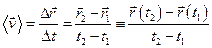Бачимо, що вектор 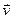співпадає за напрямом з вектором .

Введемо тепер миттєве значення вектора швидкості точки, як границю відношення 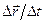при тому, що 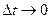, тобто

.

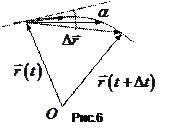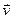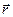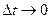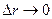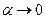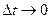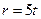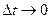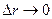Це означає, що вектор швидкості в даний момент часу дорівнює похідній від радіуса-вектора по часу і направлений по дотичній до траєкторії в напрямку руху точки. Сказане ілюструє рис.6, з якого видно, що при , , та . Але відношення може не дорівнювати нулю при (наприклад, при , , але ).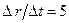

З означення швидкості випливає співнаправленість вектора швидкості і елементарного (за нескінченно малий час) переміщення: .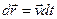

Модуль вектора швидкості 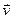дорівнює

.

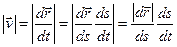Оскільки довжини хорди і дуги співпадають для нескінченно малих переміщень, тобто , з останнього рівняння одержимо

.

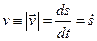Тоді 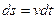, а введений раніше шлях, як довжина дуги траєкторії буде визначатися інтегралом за часом від модуля вектора швидкості

.

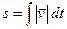Рух характеризується також прискоренням. Вектор прискорення характеризує швидкість зміни швидкості:

,

тобто дорівнює похідній від вектора швидкості по часу. Напрям вектора співпадає з напрямом вектора – приросту вектора 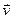за час (рис.7). Модуль вектора визначається аналогічно модулю вектора швидкості .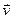

Знаючи залежність від часу проекцій радіуса-вектора , , 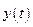, 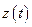можна знайти положення точки 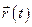в любий момент часу, а також швидкість і прискорення. Дійсно, диференціюючи по часу радіус-вектор 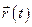, заданий виразом, одержимо

.

Проектуючи цей вираз на вісь 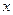, потім на осі і 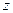одержимо відповідні проекції вектора швидкості:

Аналогічні співвідношення одержимо для вектора прискорення:

.

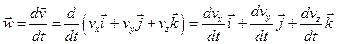Проекції вектора мають вигляд:

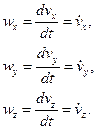
Використовуючи останні співвідношення можна записати

Аналогічний вигляд мають і . Тоді

.

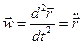Модулі векторів 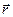, 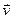і визначаються аналогічно тому, як визначається, наприклад, модуль вектора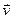

.

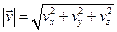Щоб характеризувати напрямки векторів вказують напрямляючі косинуси, які, наприклад, для радіуса-вектора 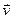, визначаються формулами

, , .

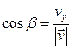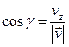Тут 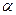, , 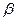, 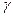– кути між вектором 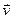і осями 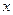, , , 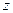відповідно. Аналогічні формули можна одержати для визначення напрямків векторів 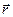і .

Таким чином, залежності , , 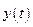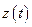повністю визначають рух точки. Знаючи їх можна знайти не тільки положення точки, а і проекції її швидкості і прискорення, а значить, модуль і напрям векторів 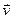і в любий момент часу.

Розв’язок оберненої задачі. По відомому значенню проекцій 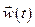, тобто знаючи прискорення, можна знайти проекці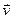ї і 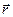, але для цього треба крім 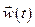знати ще і початкові умови, а саме 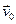і 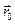в деякий початковий момент часу .

Щоб переконатися в цьому розглянемо простий приклад. Нехай відоме прискорення 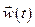точки, яка рухається прямолінійно.

Знайдемо спочатку швидкість точки 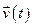. Згідно з приріст швидкості за проміжок часу дорівнює

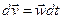
Проінтегрувавши цей вираз по часу від до , знайдемо приріст вектора швидкості 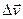за цей час

.

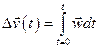Але приріст 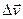– це ще не сама швидкість 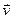. Щоб знайти 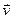, необхідно знати швидкість 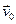в початковий момент часу. Тоді

.

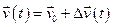Аналогічно розв’язується питання про знаходження радіуса-вектора 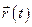точки. Перепишемо рівняння у вигляді

.

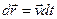Інтегруючи це рівняння з врахуванням знайденої залежності 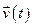, визначимо приріст радіуса-вектора за проміжок часу від до :

.

Як бачимо для знаходження самого радіуса-вектора 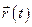необхідно знати ще положення точки 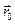в початковий момент часу. Тоді

.

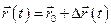Тут вважається знайденим в результаті інтегрування.

Отже, для розв’язку задачі про рух матеріальної точки, недостатньо знати залежність 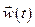, необхідно ще знати і початкові умови, швидкість 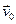і положення 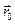в початковий момент часу.

Механічний стан частинки саме характеризується її положенням 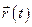і швидкістю .

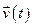Використаємо природній спосіб опису механічного руху та знайдемо тангенціальну (напрямлену вздовж траєкторії) та нормальну (перпендикулярну до траєкторії) складові вектора прискорення.

Дата добавления: 2014-01-06