Введемо для спрощення нові змінні

Чим вище степінь n поліному, що відображує частотну характеристику, тим ефективніше результат корекції за Баттервортом. 3і зростанням n у межах смуги пропускання підсилення все менше змінюється з частотою, а за її межами різче спадає до нуля.

Вираз (1.5) використовується для математичного опису реальних частотних характеристик. Таку операцію називають апроксимацією характеристик за Баттервортом. Квадрат модуля комплексної функції 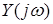можна подати у вигляді

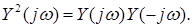
Тоді переходячи від до комплексної змінної р, отримаємо для (1.5)

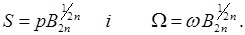
Тоді

Легко перевірити, що всі перші 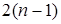похідні від при дорівнюють нулю, тобто відповідно з (1.2) функція, коректована за Баттервортом максимально плоска.

Знайдемо положення полюсів функції, коректованої за Баттервортом. Для цього необхідно розв'язати рівняння Як комплексне число, S можна подати у вигляді модуля та аргумента. У даному випадку модуль дорівнює одиниці, тоді

де k – будь–яке ціле число. Отже, розв'язок рішення для полюсів залежно від знака рівняння має вигляд:

якщо n – непарне,

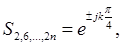
якщо n – парне,

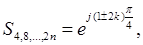(1.6)

Таким чином, усі полюси функції 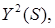коректованої за Баттевортом, знаходяться на колі одиничного радіуса поділеного однаковими кутовими відстанями, рис.1.2 (а).

Вони знаходяться як у лівій, так і у правій напівплощині комплексної змінної. Але необхідно мати на увазі, що аналізована функція є не функцією коефіцієнта передачі 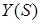, а квадратом її "модуля"

Отже, необхідну карту полюсів функції 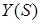можна дістати з рис.1.2 (а), якщо виключити з неї полюси, що належать до 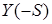і лежать у правій напівплощині.

Здобуті таким чином карти полюсів 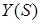для зображені на рис.1.2 (б, в, г). Щоб перейти від нормованої частоти 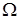до звичайної необхідно масштаб на рис.1.2 поділити на нормувальний множник 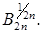Отже, всі корені 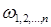лежать на колі з радіусом Цей радіус визначає значення граничної частоти , якщо її знаходити за рівнем послаблення –3дБ.

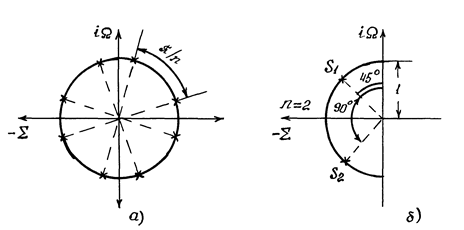
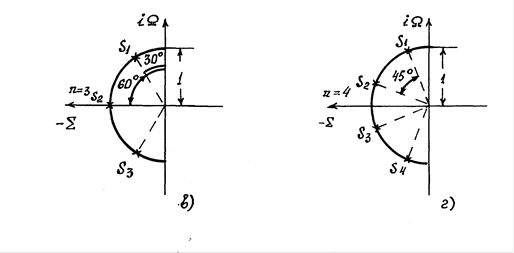
Рисунок 1.2 – Карти полюсів

Використовуючи (1.6) та враховуючи полюси, що знаходяться тільки у лівій напівплощині, можна дістати аналітичний запис функції коректованої за Баттервортом

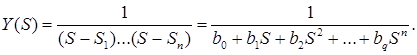
Коефіцієнти 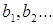знаходяться, розкриваючи дужки та об'єднуючи члени однакових степенів S. Їх також можна здобути аналітично, якщо скористуватися рівняннями

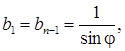
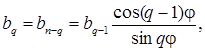
де

У випадку корекції частотних чи фазових характеристик за Брауде нуль–полюсна карта показує оптимальне положення не тільки полюсів, а й нулів.

Щоб з'ясувати це оптимальне положення, розглянемо коефіцієнт передачі, використовуючи його нулі та полюси:

(1.7)

де – нулі функції 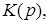а 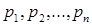– її полюси.

Припустимо, що всі полюси знаходяться на дійсній осі. Модуль коефіцієнта передачі можна подати у вигляді добутку частотних характеристик, що відповідають кожному полюсу. Якщо не враховувати нулі , то маємо

На рис.1.3(а) пунктирною прямою показані складові логарифмічної характеристики, що обумовлені кожним з полюсів, суцільною прямою – результувальна частотна характеристика.

З рис.1.3(а) можна бачити, що смуга пропускання практично визначається положенням найближчого до уявної осі полюса Отже, якщо в системі можна здійснити корекцію, яка створить окремий нуль то для ефективної корекції його необхідно розмістити там же де, і полюс 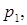тобто сумістити полюс з нулем 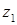, рис. 1.3 (б). Суміщення його, наприклад, з полюсом практично не розширить смуги, а тільки зменшить падіння частотної характеристики у межах від до . Якщо застосовуючи корекцію можна одержати два нулі – 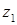та – то ними, як можна бачити з рис. 1.3 (б), необхідно компенсувати два найближчих до уявної осі полюси та Компенсація елементами корекції всіх полюсів неможлива, бо призводить до системи з фізично недосяжною необмеженою смугою пропускання.

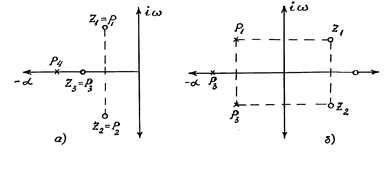На рис.1.4(а) показано випадок положення полюсів для оптимальної корекції.

У цьому випадку необхідно, у першу чергу, сумістити нулі з полюсами, найближчими до уявної осі, і, якщо полюси комплексні, тоді і компенсувальні нулі виявляються також комплексними.
При компенсації полюсів нулями відповідні пари нулів та полюсів у виразі (1.7) скорочуються, і вираз для частотної характеристики спрощується.

Оптимальне положення нулів та полюсів на рис. 1.4(а) відповідає системі мінімально–фазового типу, бо всі особливі точки розміщені в лівій напівплощині.

Здійснюючи корекцію iз залученням немінімально–фазових ланок, одержимо положення нулів та полюсів, що показані на рис. 1.4(б). У цьому випадку нулі, що корегують характеристику, як і раніше мають однакові з полюсами дійсні та уявні частини, але знак останніх для нулів додатний. Використовуючи такі ланки, можна здобути ідеальну частотну характеристику у широкому діапазоні частот. Фазовий зсув у такій ідеально–коригованій системі лишається залежним від частоти, тому включення подібних ланок у тракт підсилення, не змінюючи його частотних властивостей, дозволяє змінити його фазову характеристику. Такі ланки називають фазовими коректорами.

Розглянемо випадок, коли система має два комлексно–поєднаних полюси, а корекція можлива тільки з використанням одного нуля. У цьому випадку

де

Для спрощення подальших записів пропонується зміна р та введення замість неї змінно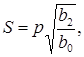ї тоді

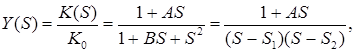
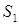де , a та 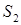– полюси

Розв'язуючи рівняння 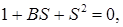знаходимо полюси При 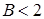полюси комплексно–поєднані. Тоді

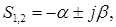
де 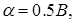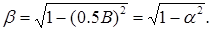Модуль коренів 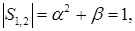тобто при будь-яких значеннях 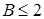полюси лежать на колі з одиничним радіусом, рис. 1.5 (а).

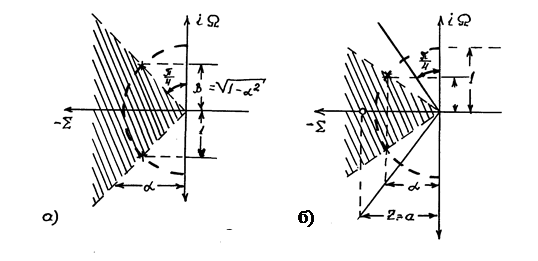Рисунок 1.5 – Зображення полюсів

Модуль частотної характеристики знаходиться після заміни S на

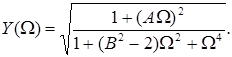
Згідно з умовою Брауде кореція має місце при 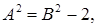або У цьому випадку може бути отримана частотна характеристика без підіймання з максимальною шириною смуги:

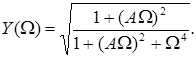
Якщо прирівняти цей вираз до 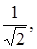можна знайти максимальну граничну частоту

Вона однозначно визначається можливою величиною при такому положенні нуля Зв'язок між 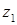та 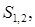що відповідає умовам корекції Брауде, має вигляд

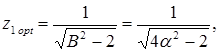
Числові значення 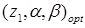та наведені у табл. 1.1.

Якщо нуль знаходиться у нескінченності, корекція за Брауде збігається з корекцією за Баттервортом. Обидва полюси при цьому розміщені на колі

Таблиця 1.1

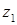
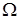
0,707 1,0 1,55

0,900 0,900 0,440 1,34

0,865 0,500 1,27

1,19 0,82 0,575 1,19

1,55 0,775 0,631 1,11

2,0 0,75 0,663 1,07

5,0 0,715 0,700 1,01

0,707 0,707 1,00

під кутом і знаходяться один від одного на кутовій відстані (рис.1.2(б) та рис.1.5(а)).

Якщо їх розташувати праворуч (відносно рис.1.5(а)), то частотна характеристика виявиться вже не максимально плоскою і на ній з'явиться нерівномірність у вигляді підйому. Якщо їх розташувати ліворуч (у межах заштрихованого сектора), то характеристики, не будучи максимально плоскими, лишаться монотонними. Поява кінцевого нуля на дійсній осі зменшує кут розташування полюсів, у межах якого зберігається монотонність частотних характеристик (заштрихований сектор на рис.1.5(б)). Конкретні співвідношення між можливими положеннями полюсів і нулів подані у табл.1.1.

Останній рядок таблиці дозволяє будувати логарифмічні частотні характеристики, використовуючи значення як точки на осі частот, після якої вони одержують нахил – 12 дБ/окт.

Усе розглянуте стосується так званої високочастотної корекції, коли внаслідок її дії смуга пропускання збільшується у бік високих частот. Часто виникає необхідність покращити частотну характеристику у області нижніх частот, тобто розширити смугу пропускання у такий спосіб, щоб пристрій ефективно підсилював низькі частоти.

Корекція, що розширює смугу пропускання в область більш низьких частот чи покращувальна характеристика у цій області, зветься низькочастотною. Частотна характеристика для області нижніх частот

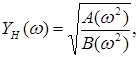
має такі особливості: 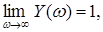отже поліноми 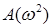та повинні мати однакові коефіцієнти при найвищих степенях і ці степені повинні бути однаковими: 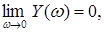отже, поліном 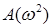не повинен містити постійного члена. Тоді

Проведемо інверсію частоти та введемо нову частоту 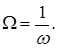Потім поділивши чисельник та знаменник на 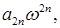дістанемо

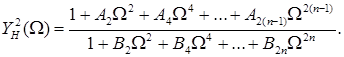
Ця форма запису характеристики тотожна тій, що розглянута вище. Отже, до неї застосовується все те, що раніше було запропоновано до ВЧ корекції. Розширення смуги пропускання, тобто збільшення у цьому випадку буде в дійсності означати розширення смуги пропускання у бік нижніх частот (зниження 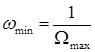). У такий спосіб "інверсією частоти" користуються не тільки при аналізі схем НЧ корекції, але і при їх синтезі.

1.3 Корекція характеристик за допомогою коригувальних індуктивностей

Каскад з індуктивною корекцією показано на рис.1.6 (а).

Рисунок 1.6 – Паралельно – індуктивна корекція

Корекція здійснюється за допомогою L, що включається послідовно з навантаженням. Така корекція зветься двополюсною або паралельною ВЧ корекцією. Розширення смуги частот у цьому випадку пояснюється тим, що коригуюча індуктивність L, навантаження та повна ємність каскаду утворюють резонансний контур. На низьких та середніх частотах навантаження транзистора практично дорівнює На ВЧ 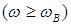при відповідному виборі резонансної частоти та резонансного опору можна дістати підсилення тоді як у звичайних каскадах на цих частотах воно вже суттєво менше за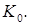

Індуктивність L впливає на властивості каскаду тільки в області верхніх частот, тому розрахункові формули для області НЧ та СЧ лишаються без змін. Еквівалентна схема каскаду для верхніх частот показана на рис.1.6(б). Щоб здобути широку смугу, опір навантаження транзистора вибирається невеликим. Це дозволяє не враховувати в еквівалентній схемі великі опори 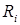та При цьому підсилення каскаду на середніх частотах

На ВЧ навантаження каскаду являє собою резонансний контур, що має провідність

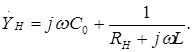
Підсилення на ВЧ відповідно становить

Для спрощення запису позначимо: – стала часу некоректованого каскаду; 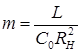– коефіцієнт корекції, що дорівнює квадрату добротності резонансного контуру.

Тоді

Комплексна частотна характеристика каскаду

Модуль її дає АЧХ каскаду

(1.8)

Аргумент визначає ФЧХ

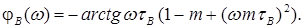(1.9)

У випадку, коли та 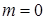вирази (1.8) та (1.9) визначають АЧХ та ФЧХ звичайного резисторного каскаду.

Знайдемо коефіцієнт корекції, що забезпечить найбільше розширення смуги без підйому частотної характеристики (оптимальна частотна характеристика).

Згідно з Брауде запишемо у вигляді відношення двох поліномів зі зростаючими ступенями частоти:

Для корекції необхідно забезпечити або звідки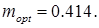

У випадку, коли 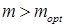на АЧХ виникає підйом, що зростає зі зростанням m. Одночасно з цим має місце незначне зростання смуги частот. На рис.1.7 побудовані АЧХ каскаду для деяких значень m.

Користуючись ними неважко побачити на скільки розширює смугу резисторного каскаду введення корекції, чому дорівнює підйом і т.і. Звичайно, смуга оцінюється на рівні Тоді для 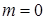маємо

Рисунок 1.7 – АЧХ каскаду для значень m

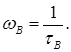Якщо гранична частота збільшується до значення Відношення 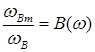показує у скільки разів розширюється смуга каскаду з корекцією. Залежність 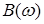подана на рис.1.8.

Рисунок 1.8 – Графіки розширення смуги каскаду з корекцією

Ці графіки побудовані при використанні (1.8) і дозволяють знайти величину підйому частотної характеристики та безрозмірну частоту 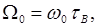на якій спостерігається цей підйом. Як можна бачити з графіків, розширення смуги при 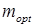складає 1,73. Подальший зріст m збільшує смугу незначно, максимальне розширення складає приблизно 1.82. Підйом частотної характеристики можна використати для компенсації спадання АЧХ попереднього або наступного каскаду.

Площа підсилення каскаду з корекцією

збільшується у разів.

Це збільшення площі можна використати або для розширення смуги частот, або для підвищення підсилення. У першому випадку за вибраним значенням на рис. 1.8 знаходять m і зберігають без зміни навантаження Тоді смуга каскаду розширюється у разів, а потрібна для корекції індуктивність дорівнює 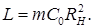У другому випадку за вибраним значенням знаходять m і, збільшивши навантаження до 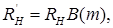одержують підсилення 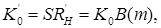тобто у разів більше. При цьому смуга частот зберігається без змін, тому що

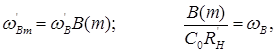
а необхідна індуктивність коректування

Аналіз показує, що при збереженні повної ємності каскаду (для польового транзистора) без змін, ніякими ускладненнями навантаження неможливо розширити смугу частот більше, ніж у 2 рази. Для каскадів на біполярних транзисторах цього о6меження немає, бо для них крутість та ємність, що шунтує навантаження, не лишаються постійними, а зменшуються з частотою. Отже, навіть така проста двополюсна корекція за допомогою тільки індуктивності дає результат, що мало відрізняється від граничного. Це свідчить про високу ефективність схеми і зумовлює її широке застосування.

Поряд з паралельною індуктивною ВЧ корекцією знаходить своє застосування і послідовна індуктивна ВЧ корекція, рис. 1.9.

Рисунок 1.9 – Послідовна індуктивна ВЧ корекція

В цьому випадку індуктивність коректування включається послідовно з розділовою ємністю. Еквівалентна схема каскаду з такою корекцією наведена на рис. 1.10.

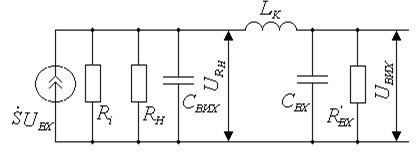
Рисунок 1.10 – Еквівалентна схема каскаду з послідовною індуктивною ВЧ корекцією

Повна паразитна ємність при такому включенні індуктивності коректування поділяється на дві частини і , у результаті чого загальна паразитна ємність дорівнює

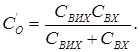
Паралельний резонансний контур, що утворюється 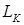і має резонансну частоту

тобто ця частота вище, ніж в схемі з паралельною ВЧ корекцією (якщо значення 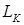однакові).

На частоті опір навантаження каскаду є опором паралельного контуру ІІІ виду, який частково шунтується опорами і

Визначимо опір навантаження каскаду на резонансній частоті 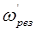. Враховуючи, що і (для ПТ), то шунтувальною дією 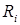i на еквівалентний резонансний опір контуру можна знехтувати. В цьому випадку

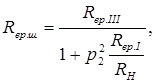
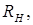Оскільки паралельно частині контуру підключено опір то величина і викиду АЧХ на частоті паралельного резонансу 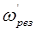не спостерігається, але викид АЧХ може спостерігатися на частоті послідовного резонансу 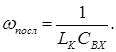Оскільки контур ІІІ виду має три реактивності і напруга виходу знімається з реактивного елемента (напруга збудження цього контуру 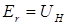) послідовного контуру 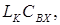то вихідна напруга 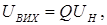і відповідно коефіцієнт підсилення на частоті може бути більшим за

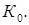
Для більш ефективного згладжування АЧХ часто застосовують опір шунтування що підключається паралельно до індуктивності коректування

Застосовуючи сполучення схем паралельної і послідовної ВЧ корекціі (складна корекція), можна досягнути більш широкої смуги пропускання і рівномірності коефіцієнта підсилення у досить широкій смузі.

1.4 ВЧ корекція характеристик за допомогою зворотного зв'язку

Як приклад застосування ВЗЗ для корекції АЧХ підсилювача розглянемо схему емітерної (витокової) ВЧ корекції, рис.1.11.

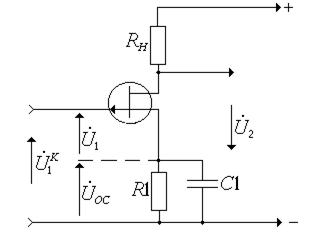
Рисунок 1.11 – Емітерна (витокова) ВЧ корекції

Ця корекція використовує ВЗЗ послідовного типу за струмом. Провідність у колі емітера вибирається таким чином, щоб у смузі НЧ та СЧ вона була активною і досить малою. Ця умова буде виконуватись у випадку Завдяки цьому у смузі НЧ та СЧ діє сильний ВЗЗ і підсилення значно зменшено. З ростом частоти шунтувальна дія ємності зростає, 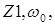ВЗЗ зникає, і зменшення коефіцієнта підсилення, що має місце з ростом частоти, компенсується зменшенням ВЗЗ. Таким чином, зменшуючи підсилення на НЧ та СЧ і зберігаючи його рівень на ВЧ можна отримати рівномірне підсилення у широкій смузі частот.

Коефіцієнт підсилення каскаду з ВЧ корекцією у смузі ВЧ дорівнює

(1.10)

де – стала часу кола ЗЗ (коректувального кола) – глибина ВЗЗ для НЧ і СЧ (випадок витокової корекції).

Вводячи узагальнену частоту зведемо вираз (1.10) до вигляду

де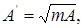

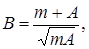
Згідно з умовою Брауде оптимальна (максимально плоска без підйому) АЧХ буде мати місце при виконанні умови

Дата добавления: 2014-01-06