Дисперсия случайной функции

Рассмотрим случайную функцию X (t). При фиксированном значении аргу­мента, например при t = t₁, получим сечение - случайную величину X (t₁) с дисперсией D [ X(t₁) ] 0 (предполагается, что дисперсия любого сечения существует). Таким образом, каждое фиксированное значение аргумента определяет сечение - случайную величину, а каждой случайной величине соответствует ее дисперсия. Отсюда следует, что каждому фиксированному значению аргумента t соответствует определенная дисперсия; это означает, что дисперсия случайной функции есть функция (неслучайная, причем неотрицательная) от аргумента t; ее обозначают через D_x(t). В частном случае D_x (t) может сохранять постоянное значение при всех допустимых значениях аргумента. Дадим теперь определение дисперсии.

Определение 2.3. Дисперсией случайной функции X(t) называют неслучайную неотрицательную функцию D_x(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии сечения, соответствующего этому же фиксированному значению аргумента:

D_x(t)=D [ X(t) ].

Дисперсия характеризует степень рассеяния возможных реализаций (кривых) вокруг математического ожидания случайной функции («средней кривой»). При фиксированном значении аргумента дисперсия характеризует степень рассеяния возможных значений (ординат) сечения вокруг математического ожидания сечения («средней ординаты»).

Часто вместо дисперсии рассматривают среднее квадратичное отклонение случайной функции, которое определяют по аналогии со средним квадратичным отклонением случайной величины.

Средним квадратичным отклонением случайной функции называют квадратный корень из дисперсии:

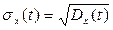
Свойства дисперсии случайной функции.

Используя свойства дисперсии случайной величины, легко получить свойства дисперсии случайной функции.

Свойство 1. Дисперсия неслучайной функции j(t) равна нулю:

Свойство 2. Дисперсия суммы случайной функций X(t) и неслучайной функции j(t) равна дисперсии случайной функции:

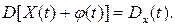
Свойство 3. Дисперсия произведения случайной функции X(t) на неслучайную функцию j(t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции:

Пример 2.2. Найти дисперсию случайной функции X(t) = Usin t, где U - случайная величина, причем D(U) = 6.

Решение. Найдем дисперсию, приняв во внимание, что неслучайный множитель sin t можно вынести за знак дисперсии, возведя его в квадрат:

D [ X(t) ] = D [ U sin t ] = sin² tD(U) = 6sin² t. Итак, искомая дисперсия D [ X(t) ] =6sin² t.

Математическое ожидание и дисперсия характеризуют случайную функцию далеко не полно. Можно привести примеры двух случайных функций, которые имеют одинаковые математические ожидания и дисперсии, но поведение которых различно. Зная лишь эти две характеристики, в частности, ничего нельзя сказать о степени зависимости двух сечений. Для оценки этой зависимости вводят новую характеристику - корреляционную функцию. Далее покажем, что, зная корреляционную функцию, можно найти и дисперсию; поэтому знать закон распределения для отыскания дисперсии нет необходимости. Уже это обстоятельство указывает на целесообразность введения корреляционной функции.

Определение 2.4. Ковариационной функцией n -мерного случайного процесса , называют матричную функцию типа n х n двух скалярных переменных t₁ и t₂ значение которой при фиксированных 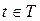равно ковариации двух случайных векторов 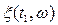и определяемой следующим образом:

,

где и - двумерная функция плотности вероятностей (возможно обобщенная) исходного случайного процесса.

Прежде чем перейти к дальнейшему изложению, введем следующие понятия.

Определение 2.5. Центрированной случайной функцией называют разность между случайной функцией и ее математическим ожиданием:

.

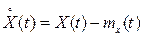Дата добавления: 2014-01-07