Магнитный поток. Закон электромагнитной индукции. Потокосцепление

Напряженность магнитного поля. Магнитодвижущая сила.

Магнитный поток. Закон электромагнитной индукции. Потокосцепление.

Лекция 3. Основные понятия теории магнитного поля

Поток вектора магнитной индукции сквозь некоторую поверхность 5 (рис. 1.23) называют кратко магнитным потоком сквозь эту поверхность и обозна­чают Ф.

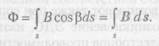
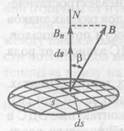
Магнитная индукция является плотностью магнитного потока в данной точ­ке поля. Действительно, проведя поверхность нормально к вектору В, будем иметь cos р = 1; d<& - В ds; В - d<$/ds.

Единицей магнитного потока является вебер (Вб). Едини­цей магнитной индукции — тесла, равная веберу па квадрат­ный метр (1 Тл = 1 Вб/м²).

Линиями магнитной индукции называют линии, прове­денные так, чтобы касательные к ним в каждой их точке сов­падали по направлению с вектором В. Эти линии изобража­ют со стрелками, указывающими направление вектора В.

Часть пространства, ограниченная трубчатой поверхно­стью, образованной совокупностью линий магнитной индук­ции, называется трубкой магнитной индукции.

Можно представить все магнитное поле подразделенным на трубки магнитной индукции и условиться изображать каждую такую трубку одной линией магнит­ной индукции, совпадающей с осью трубки.

Трубки магнитной индукции, поток сквозь поперечное сечение которых ра­вен единице, называются единичными трубками. Соответственно линии магнитной индукции, изображающие единичные трубки, называются единич­ными линиями магнитной индукции.

Принцип непрерывности магнитного потока, имеющий в теории электромаг­нитных явлений фундаментальное значение, гласит, что линии магнитной ин­дукции нигде не имеют ни начала, ни конца — они всюду непрерывны.

Мы убеждаемся в справедливости этого важного принципа во всех без исклю­чения случаях, когда магнитное поле существует в воздухе или вообще в такой среде, в которой поле может быть непосредственно исследовано опытным путем. Так, например, линии магнитной индукции около прямолинейного провода с то­ком являются окружностями, имеющими центры на оси провода (рис. 1.24). Направление линий связано с направлением тока правилом правого винта. На рис. 1.24 изображено нормальное сечение провода, причем ток уходит от наблю­дателя, что показано косым крестом, изображающим хвост стрелки. В том слу­

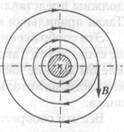чае, когда ток направлен на наблюдателя, ставят условную точку, изображающую острие стрелки.

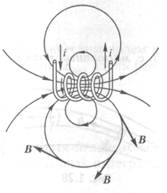
Как бы ни была сложна форма контура электрического тока, линии магнитной индукции, окружающие этот кон­тур, всегда оказываются непрерывными. В виде примера можно указать поле соленоида с током, картина линий ко­торого изображена на рис. 1.25.

Требует особого рассмотрения вопрос о непрерывности линий магнитной индукции в том случае, когда в магнит­ном поле расположены твердые тела и мы лишены воз­можности непосредственно исследовать поле внутри этих тел. Так, например, поле постоянного магнита изучить не­посредственно опытным путем можно только в пространстве вне магнита. Поэтому необходимо установить на основе каких-либо допол­нительных фактов или каких-либо соображений, продолжаются ли линии магнитной индукции и внутри тела самого магнита. Дей­ствительно, существование поля вне магнита можно было бы объяснить наличием на поверхности полю­сов магнита особых источников магнитного поля, на­зываемых магнитными массами. Согласно та­кому представлению, на северном полюсе магнита, где, как нам кажется, начинаются линии магнитной индукции, должна быть расположена положительная магнитная масса, и на южном, где линии кончаются -отрицательная магнитная масса. Такое представление о природе магнитных явлений и сложилось историче­ски до эпохи, началом которой явилось открытие маг­нитного поля электрических токов.

Если бы поле создавалось магнитными массами т, то поле внутри магнита должно было бы выглядеть так, как это изображено на рис. 1.26, — линии маг­нитной индукции внутри магнита, так же как и вне его, оказались бы направлен­ными от северного полюса к южному.

В настоящее время намагниченность магнита, или вообще намагниченность тела, объясняют существованием элементарных токов внутри вещества тела, являющихся результатом движения электронов по орбитам в атомах, а также

существованием магнитных моментов эле­ментарных частиц. Хотя внутреннее строе­ние элементарных частиц и, соответственно, природа их магнитных моментов в настоя­щее время еще не изучены, но можно вы­сказать предположение, что и магнитные моменты элементарных частиц являются ре­зультатом внутреннего движения в этих час­тицах, имеющего характер электрических токов.

Исходя из этих представлений, приходим к заключению, что внутри магнита линии магнитной индукции должны идти так же, как в соленоиде (см. рис. 1.25), — они должны представлять собой продолжение линий, расположенных вне магнита. Такая правильная картина поля изображена на рис. 1.27.

Эти соображения приводят к выводу, что магнитных масс в действительности не существует. Такой вывод подтверждается опытом с ломанием магнита. На ка­кие бы мелкие части ни дробили магнит, никогда невозможно получить такие его части, на которых наблюдалось бы наличие избытка магнитной массы одного знака.

Все эти соображения остаются в силе по отношению к любому телу, через ко­торое проходит магнитный поток.

Итак, магнитное поле всегда связано с электрическим током. Во всех без ис­ключения случаях линии магнитной индукции непрерывны.

Математически принцип непрерывности магнитного потока формулируется следующим образом:

т. е. магнитный поток сквозь любую замкнутую поверхность равен нулю.

В § 1.8 было высказано общее положение, что если линейный интеграл на­пряженности электрического поля вдоль замкнутого контура не равен нулю, то в контуре действует ЭДС, равная этому интегралу. Таким образом, последнее равенство свидетельствует, что во всех случаях, когда магнитный поток Ф, проходящий сквозь поверхность, ограниченную некоторым контуром, изменяется во времени, в этом контуре индицируется ЭДС, равная взятой со знаком минус скорости изменения этого потока:

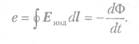
но в проводящей среде и частично в диэлектрике. Во всех без исключения слу­чаях при изменении во времени магнитного потока сквозь поверхность, огра­ниченную любым контуром, в последнем возникает ЭДС. В проводящей среде ЭДС может вызвать токи проводимости, в диэлектрике переменная ЭДС вызы­вает токи электрического смещения. При таком обобщении равенство (**) сви­детельствует, что при изменении во времени магнитного поля появляется в том же пространстве связанное с ним электрическое поле, причем электрическое напряжение вдоль любого замкнутого контура равно ЭДС, индуцируемой в этом контуре.

По сути дела, оба эти поля — магнитное и электрическое — являются при этом двумя сторонами единого электромагнитного поля.

Понимаемое в таком широком смысле уравнение (**) является одним из ос­новных уравнений электромагнитного поля.

В случае, когда контур образован проводником, в нем под действием ЭДС возникает ток проводимости, и этот ток создает вокруг контура свое магнитное поле. При этом Ф в выражении (**) является потоком, созданным внешними источниками и током i в самом контуре. Если в контуре нет других источников ЭДС, а именно сторонних ЭДС, рассмотренных в § 1.8, то и для напряженности результирующего ноля Е имеем

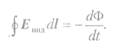
Величина &E_Hmdl есть сумма падений напряжения вдоль всего замкнутого кон­тура, равная току i в контуре, умноженному на электрическое сопротивление г контура. Следовательно, в этом случае

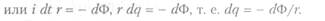
Для конечного изменения потока на величину ДФ получаем

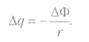
В этой форме закон электромагнитной индукции и был установлен экспери­ментально Фарадеем.

Магнитный поток Ф сквозь поверхность s, ограниченную контуром, например контуром проводящей цепи, равен поверхностному интегралу вектора магнит­ной индукции, распространенному по поверхности s: Ф = f В ds. Это выражение

S

справедливо для любой поверхности, ограниченной сколь угодно сложным кон­туром. В общем случае такая поверхность может иметь весьма сложную форму. Так, на рис. 1.31 штриховкой показана поверхность, «натянутая» на контур, рас­положенный по винтовой линии и образующий катушку из трех витков. Отдель­ные линии магнитной индукции пронизывают эту поверхность несколько раз: линии 4, 5, 6, 7 и 8 — три раза, линия 3 — два раза.

Целесообразно в таких сложных случаях ввести понятие о потокосцеп-л е н и и У. Термин «потокосцепление» необходимо ввести в связи с тем, что от-

дельные линии магнитной индукции несколько раз сцепляются со всем контуром. Значение Ч* можно получить, умножая поток каждой единичной ли­нии магнитной индукции на число витков цепи, с которыми она сцепляется, и складывая получен­ные результаты. Сложение следует производить ал­гебраически, причем положительными следует счи­тать линии магнитной индукции, направление ко­торых связано с положительным направлением то­ка в контуре электрической цепи правилом право­го винта.

Ясно, что ЭДС, индуцируемая во всей цепи, определяется потокосцеплени-ем Ч*. Действительно, при уменьшении потока до нуля каждая линия магнитной индукции столько раз пересечет контур тока, сколько раз она с ним сцепляется. Поэтому должно быть равенство

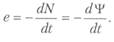
Потоки, сцепляющиеся с отдельными витками катушки, различны. Поэтому различны и ЭДС, индуцируемые в отдельных витках. В ряде случаев прибли­женно можно считать, что все линии магнитной индукции сцепляются со всеми w витками катушки. Тогда потокосцепление катушки связывается с потоком Ф в одном витке простым соотношением 4^х - даФ. В таком случае ЭДС, индуцируе­мая в катушке,

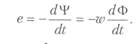
Таким упрощенным расчетом обычно можно пользоваться при вычислении ЭДС, индуцируемых в катушках с замкнутыми сердечниками из ферромагнит­ных материалов.

В простейшем случае для одного контура с электрическим током магнитный поток, сцепляющийся с этим контуром, определяется током г, протекающим в этом же контуре. Такой поток называют потоком самоиндукции. Потокосцепление самоиндукции некоторого электрического контура или, что то же, некоторой неразветвленной электрической цепи, обозначают y_L. Мож­но представить его в виде

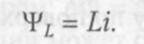
Величину L называют собственной индуктивностью или просто индуктивностью контура. Индуктивность зависит от геометрических вели­чин g, определяющих размеры и форму контура, а также от абсолютной магнит­ной проницаемости ц среды, в которой существует магнитное поле: L = F(g, ц). Для однородной среды с ц = const имеем L = nf(g).

При изменении потока самоиндукции в контуре возникает электродви­жущая сила самоиндукции. Изменение потока *Ґ_L может происходить как вследствие изменения тока, так и вследствие изменения индуктивности. По­этому в общем случае ЭДС самоиндукции e_L может быть представлена в виде суммы двух членов:

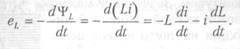При L = const

Для двух или нескольких контуров с токами магнит­ный поток, сцепляющийся с одним из этих контуров, оп­ределяется токами во всех контурах. Рассмотрим два кон­тура и предположим, что ток протекает только в первом из них (рис. 1.32). Может оказаться, что часть линий маг­нитной индукции потока самоиндукции первого контура сцепляется также и со вторым контуром. При этом поток, сцепляющийся со вторым контуром и определяемый то­ком в первом контуре, называют потоком взаимной индукции. Потокосцепление взаимной ин­дукции со вторым контуром будем обозначать Ч₂м ^или У21. Первый индекс всегда будет указывать, с какой це­пью рассматривается сцепление потока. Второй индекс

(М или 1) указывает, что поток определяется током, протекающим в другой, в данном случае в первой, цепи. Можно написать

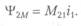
Величину М₂₁ называют взаимной индуктивностью контуров. Она зависит от геометрических величин g, определяющих размеры и формы конту­ров и их взаимное расположение, а также от абсолютной магнитной проницае­мости ц среды: М = f(g, ц). Если ц = const, то М = (J/(g).

Единицей индуктивности и взаимной индуктивности является генри (Гн).

При изменении потока взаимной индукции, сцепляющегося со вторым кон­туром, в этом контуре возникает электродвижущая сила взаимной и н д у к ц и и. Поток ^9^ может изменяться либо вследствие изменения тока ц, либо вследствие изменения взаимной индуктивности М₂₁. Соответственно, ЭДС взаимной индукции, возникающая во втором контуре, может быть представлена в виде

Остановимся еще на общем характере индуцированных ЭДС. Знак «минус» в выражении для индуцированной ЭДС" свидетельствует о том, что эта ЭДС стре­мится вызвать токи, направленные таким образом, чтобы воспрепятствовать изменению магнитного потока. Это положение выражает сформулированный Ленцем принцип э л е к т р о м а г н и т н о и и н е р ц и и. В самом деле, пред­положим, что поток, сцепляющийся с контуром, убывает, т. е. d*Ґ < 0. В таком случае е = - d*Ґ/dt > 0, и следовательно, возникающая в контуре ЭДС стремится вызвать ток в положительном направлении и тем самым воспрепятствовать убы­ванию потока. Наоборот, если поток возрастает, то d*Ґ > 0 и е < 0. В этом случае ЭДС в контуре стремится вызвать ток в отрицательном направлении и этим вос­препятствовать увеличению потока. Мы видим, что индуцированные ЭДС име­ют характер сил инерции.

На основании сказанного можно сформулировать принцип электромагнитной инерции в отношении электромагнитных процессов, совершающихся в системе контуров с электрическими токами, а именно: в системе контуров с электриче­скими токами существует тенденция к сохранению неизменными магнитных по­токов, сцепляющихся с отдельными контурами системы. При всякой попытке изменить потоки, сцепляющиеся с контурами, в контурах возникают электро­движущие силы, стремящиеся воспрепятствовать этому изменению. В простей­шем случае для одного контура с током возникает ЭДС самоиндукции, равная

В простейшем случае, который рассматривается в динамике, а именно, при движении свободной материальной точки, принцип инерции заключается в том, что свободной материальной точке свойственно сохранять свое количество дви­жения. Если под действием внешних сил изменяется количество движения точ­ки, то, вводя в рассмотрение силы инерции, равные и противоположные внеш­ним силам, можно рассматривать эти силы инерции как препятствующие изменению количества движения. Если направление силы совпадает с направле­нием скорости v, то сила инерции имеет выражение

где т — масса материальной точки.

Мы видим, что магнитный поток можно рассматривать как количество дви­жения в электромагнитном процессе, индуктивность контура — как коэффици-

Дата добавления: 2014-01-07