Курс физики

Физические основы механики,

молекулярная физика и термодинамика

ОПОРНЫЙ КОНСПЕКТ

1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

1.1. Введение. Предмет и задачи физики

Физика изучает наиболее общие формы движения материи (механические, тепловые, электромагнитные и т.д.) и их взаимные превращения. Эти формы движения имеют место во всех высших и более сложных формах движения (химических, биологических процессах и т.п.) и неотделимы от них.

За последние десятилетия физика разрослась и разветвилась. Этот процесс нашел отражение в появлении таких областей, как астрофизика, биофизика, геофизика, радиофизика, кристаллофизика и т.д. Эта дифференциация, тем не менее, не привела к потере физикой единства фундамента, общности методов исследования. В настоящее время физика развивается не в направлении измерений, вычислений, технических разработок, а ставит вопросы о возможности создания новых материалов, раскрытия неизвестных явлений.

Возникли физические направления, которые в корне изменяют технику. Это получение энергии за счет термоядерных реакций, развитие лазерной техники, создание магнито-гидродинамических (МГД) генераторов, Таким образом, физика и техника оказывают взаимное влияние друг на друга.

Механика - учение о простейшей форме движения материи. Движение представляет собой форму существования материи и, в философском смысле, движение - это всякое изменение материи.

Механика изучает простейшую форму движения - перемещение материальных тел, т.е. изменение их взаимного расположения с течением времени. Простое механическое перемещение всегда сопровождает все более сложные и высшие формы движения.

Движение тел происходит как в пространстве, так и во времени (пространство и время - неотъемлемые формы существования материи).

Классическая механика, созданная в XVII - XVIII вв., описывает закономерности движения тел со скоростями, много меньшими скорости света в вакууме v<<c, и является фундаментом физики. Однако, в классической механике использовались старые метафизические представления, согласно которым пространство и время существуют независимо друг от друга, а также от материи.

В ХХ в. возникли новые, обоснованные опытом представления о взаимосвязи пространства и времени. На основе этих представлений Эйнштейном была создана “Теория относительности” - механика больших скоростей.

Движение относительно, поэтому необходимо ввести понятие “тело отсчета”, которое условно считается неподвижным и относительно которого

рассматривается движение, а связанная с ним система координат называется системой отсчета.

Движущиеся тела обладают размерами, однако, изучение основных закономерностей движения в механике проводится на простейшей модели - материальной точке. Под материальной точкой понимается объект, имеющий конечную массу и бесконечно малые размеры. Понятно, что это - абстракция: реальные физические тела имеют конечные размеры. Однако, если размерами тела можно пренебречь в условиях данной задачи, то его массу можно считать сосредоточенной в геометрической точке и само тело принять за материальную точку.

При изучении вращательного движения применяется другая модель - “абсолютно твердое тело”, т.е. тело, не подверженное деформации. Это, конечно, тоже абстракция. Реальные тела всегда более или менее подвержены деформации. Однако, если этой деформацией можно пренебречь в условиях данной задачи, то тело можно считать абсолютно твердым.

Использование простейших моделей позволяет рассмотреть основные закономерности движения.

1.2. Элементы кинематики материальной точки и

вращательного движения твердого тела

Кинематика изучает движение тел без учета причин, вызывающих это движение.

Динамика рассматривает движение тел в зависимости от причин, вызывающих это движение.

Рассмотрим произвольное криволинейное движение материальной точки, положение которой в пространстве определяется тремя координатами, которые в свою очередь являются функциями времени. Существует множество систем координат, однако мы будем пользоваться простейшей - трехмерной декартовой системой координат, представляющей собой три взаимно-ортогональные координатные оси - x, y и z (рис. 1-1).

Принято определять положение точки при помощи радиуса-вектора. Радиусом-вектором r (t) называется вектор, проведенный из начала координат в точку пространства, где в момент времени t находится материальная точка. Радиус-вектор выражается через координаты x, y и z следующим образом:

r (t) = i x + j y + k z,

где i, j и k - соответствующие орты, т.е. единичные векторы, направленные вдоль соответствующих осей.

Рис. 1-1

Геометрическими характеристиками движения являются траектория, путь, перемещение.

Траекторией называется пространственная кривая, которую описывает материальная точка, перемещаясь в пространстве.

Путь D S - это расстояние, пройденное по криволинейной траектории из начальной точки 1, в которой материальная точка находилась в момент времени t, в положение 2. Этот путь она проходит за время D t. (D S - скалярная величина).

Перемещение - это вектор D r, проведенный из точки 1 в точку 2.

Основные характеристики движения: скорость и ускорение.

Скорость характеризует быстроту перемещения материальной точки по траектории.

Средняя скорость:

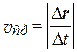. (1.1)

Мгновенная скорость:

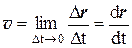(1.2)

Через проекции скорость выражается так:

.

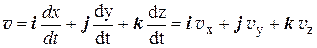Ускорение характеризует быстроту изменения скорости. В общем случае скорость может изменяться как по абсолютной величине, так и по направлению. Изменение скорости по направлению характеризуется нормальным ускорением 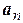. Изменение скорости по абсолютной величине характеризуется тангенциальным или касательным ускорением 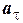. Мгновенное ускорение, т.е. ускорение в данный момент времени определяется как предел отношения приращения скорости 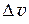к интервалу времени D t, за который произошло это приращение:

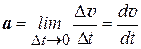. (1.3)

Пусть в точке 1 траектории скорость равна v ₁, а в точке 2 – соответственно v ₂ (рис. 1-2).

Рис. 1-2

Отложим на АС отрезок AF = v ₁ и разобьем D v на две составляющие:

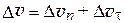. (1.4)

Тогда

, (1.5)

где

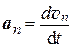, а 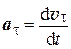. (1.6)

Можно показать, что нормальная составляющая ускорения равна

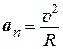(1.7)

и направлена по радиусу к центру кривизны в данной точке, а касательная составляющая ускорения равна

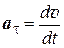
и характеризует изменение скорости по модулю.

Динамика изучает механическое движение тел и связь основных кинематических параметров движения с причинами, вызывающими это движение, т.е. с силами. Основные принципы механики сформулированы Ньютоном в виде трех законов.

Первый закон Ньютона: Существуют такие системы отсчета, относительно которых все тела, не взаимодействующие с другими телами, движутся равномерно и прямолинейно.

Этот закон называется законом инерции. Он устанавливает существование инерциальных систем отсчета, в которых выполняются второй и третий законы. Инерциальных систем отсчета может быть бесчисленное множество. Любая система отсчета, движущаяся относительно инерциальной с постоянной скоростью, также является инерциальной системой.

Основой динамики является второй закон Ньютона, который формулируется следующим образом:

Если на тело действует сила, то тело приобретает ускорение, прямо пропорциональное этой силе и обратно пропорциональное массе тела:

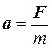. (1.8)

Второму закону Ньютона можно придать иной, более общий вид, введя понятие импульса тела (или материальной точки):

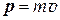. (1.9)

Это векторная величина, совпадающая по направлению с направлением вектора скорости. Она имеет еще одно название - количество движения.

Тогда

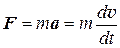. (1.10)

В классической механике считается, что масса тела не зависит от его скорости. Поэтому можно массу внести под знак производной. Выражение (1.10) приобретает вид:

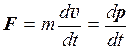. (1.11)

В таком виде этот закон выражает зависимость скорости изменения импульса тела от силы, приложенной к этому телу. Этот закон можно назвать законом изменения импульса:

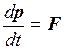. (1.12)

Закон изменения импульса может быть записан иначе:

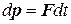. (1.13)

Слева в этом выражении стоит изменение импульса за бесконечно малое время dt. Выражение F dt в правой части (1.13) называется импульсом силы, действующей на тело за это же время.

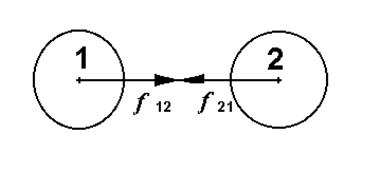
Третий закон формулируется следующим образом:

Всякое действие тел друг на друга носит характер взаимодействия. Силы, с которыми действуют друг на друга взаимодействующие тела, находящиеся в равновесии, равны по величине и противоположны по направлению (рис.1-3), т.е..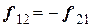

Рис. 1-3

Одним из наиболее важных законов механики является закон сохранения импульса. Рассмотрим закон сохранения импульса применительно к системе тел. Под системой тел понимается совокупность взаимодействующих тел, движение которых рассматривается совместно и одновременно.

Импульсом системы p _с называется векторная сумма импульсов N тел или N материальных точек, составляющих механическую систему:

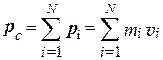. (1.14)

Силы взаимодействия между телами, составляющими систему, называются внутренними силами. Силы, действующие со стороны тел, не входящих в данную систему, называются внешними силами.

Система называется замкнутой или изолированной, если действием на нее внешних сил можно пренебречь по сравнению с внутренними силами.

Для получения закона изменения импульса системы тел возьмем производную по времени от импульса системы p _с:

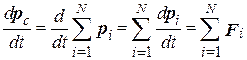. (1.15)

Последний член в этом выражении содержит только сумму внешних сил, приложенных к телам системы.

На изолированную систему внешние силы не действуют и поэтому:

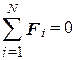и ,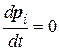

что, в свою очередь означает, что импульс замкнутой системы тел сохраняется постоянным во времени при любых процессах, происходящих в этой системе:

или: 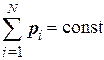. (1.16)

Это и есть закон сохранения импульса замкнутой системы материальных точек.

1.4. Работа и энергия

В школьном курсе физики работа определялась как произведение силы на пройденный путь и на косинус угла между ними:

A=FS cos a. (2.1)

Однако такое определение справедливо лишь в тех случаях прямолинейного движения, когда сила на всем пути остается постоянной по величине и направлению. Чаще встречаются случаи, когда материальная точка перемещается по криволинейной траектории, а сила на всем пути перемещения меняет свое направление и/или величину.

Пусть, например, материальная точка перемещается по криволинейной траектории от исходного положения 1 до положения 2. Определим элементарную работу на бесконечно малом участке траектории dS. Для этого вначале выделим этот участок, на котором в момент времени t находится точка. Радиус-вектор ее положения равен r (t). Вектор перемещения d S, определим как вектор, по абсолютному значению равный элементу dS, и направленный по касательной к траектории.

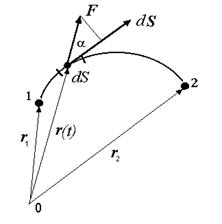
Рис.2-1

На бесконечно малом участке траектории силу F можно считать постоянной, и работу определить как скалярное произведение вектора силы F на вектор перемещения d S:

dA=( F d S)=FdS cos a. (2.2)

Работа силы F положительна dA> 0 (т.е. сила совершает работу), если 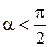, т. е. 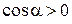. Если же 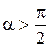, то c osa<0 и работа силы F отрицательна: dA< 0 (работа совершается против направления действия силы).

Полная работа по перемещению материальной точки из положения 1 в положение 2 определяется интегралом от dA по всему пути S:

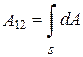. (2.3)

В качестве примера определим работу, совершаемую переменной силой при изменении скорости тела от v ₁ до v ₂. Так как работа совершается только касательной составляющей силы F _t, то:

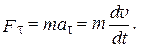(2.4)

Тогда работа силы с учетом (2.4) будет:

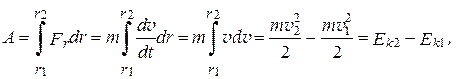(2.5)

где

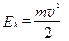(2.6)

есть кинетическая энергия, которая характеризует движение тела и зависит от его массы и скорости. А работа - это процесс взаимодействия тел, приводящий к изменению энергии системы, которая определяет состояние, т.е. совокупность свойств системы. Важно, что работа характеризует только изменение энергии, поэтому кинетическая энергия задается с точностью до произвольной постоянной С:

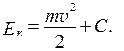(2.7)

При v =0 по отношению к данной системе отсчета следует считать E_k =0 и, таким образом, положить C =0. Тогда:

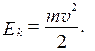(2.8)

Под механической энергией понимают сумму кинетической и потенциальной энергий. Потенциальная энергия характеризует взаимодействие тел, зависит от их взаимного расположения и действующих в системе сил, но не зависит от скорости тел. Установлено, что потенциальную энергию можно задать не для любого силового поля, а только в случае консервативных сил, работа которых не зависит от формы пути, а определяется только разностью потенциальных энергий в начальной и конечной точках пути. Примером такой силы является гравитационная сила, т.е. сила тяжести, действующая в гравитационном поле.

Рассмотрим пример: тело массы m находится в поле тяготения Земли. Определим работу, которую совершает сила тяжести при свободном падении (перемещение тела изменяется от r ₁ до r ₂). Покажем, что работа силы тяжести совершается за счет убыли потенциальной энергии тела.

Сила тяготения - переменная сила:

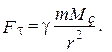(2.9)

Здесь r - расстояние от центра Земли до тела; M _з - масса Земли. Тогда элементарная работа определится следующим образом:

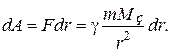(2.10)

Полная работа при перемещении тела на всем пути от r ₁ до r ₂ равна

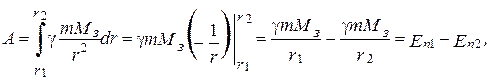(2.11)

где

(2.12)

есть потенциальная энергия тела в гравитационном поле Земли. Как видно из (2.11), работа сил тяжести совершается за счет убыли потенциальной энергии. Потенциальная энергия, как и кинетическая, задается с точностью до произвольной постоянной.

За нуль отсчета потенциальной энергии Е _п=0 принимается значение потенциальной энергии в бесконечности (т.е. при r → ∞), когда прекращается взаимодействие тел.

Закон сохранения механической энергии формулируется так: полная механическая энергия замкнутой системы, в которой действуют консервативные силы, сохраняется постоянной во времени.

Если, например, тело падает, т.е. перемещается в гравитационном поле, то сила тяжести совершает работу за счет убыли потенциальной энергии. На малом отрезке dr элементарная работа равна:

(2.13)

Однако при этом кинетическая энергия тела увеличивается, т.е. совершаемая работа идет на увеличение кинетической энергии тела:

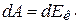(2.14)

Поскольку левые части выражений (2.13) и (2.14) равны, то равны и правые, т.е.:

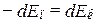(2.15)

Следовательно,

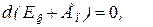(2.16)

или:

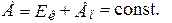(2.17)

Это и есть закон сохранения механической энергии. Убыль потенциальной энергии сопровождается равным возрастанием кинетической энергии.

Если же в системе действуют также и неконсервативные силы, например силы трения, то механическая энергия системы уменьшается и переходит в немеханические виды энергии (тепловую энергию и др.). При этом работа сил трения равна убыли механической энергии тела:

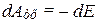. (2.18)

В таких системах выполняется общий закон сохранения: в изолированной системе сумма всех видов энергии остается постоянной.

Иллюстрацией действия законов сохранения энергии и импульса является задача об ударе шаров. Рассмотрим прямой центральный удар шаров, т.е. такой удар, при котором вектор скорости одного из шаров в момент столкновения проходит через центр тяжести другого. Возможны два крайних случая - абсолютно упругий и неупругий удары.

При абсолютно упругом ударе кинетическая энергия движения шаров полностью, без потерь переходит в потенциальную энергию деформации шаров. Шары деформируются, а затем восстанавливают свою первоначальную форму. Потенциальная энергия деформации полностью переходит в кинетическую энергию движения шаров. Если шары движутся без трения, то систему из двух шаров можно считать замкнутой и для такой системы закон сохранения импульса запишется в следующем виде:

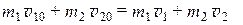, (2.19)

где

m ₁ и m ₂ - массы первого и второго шаров соответственно;

v ₁₀ и v ₂₀ - векторы начальных скоростей первого и второго шаров;

v ₁ и v ₂ - векторы скоростей обоих шаров после удара.

Одного этого уравнения недостаточно для того, чтобы найти скорости шаров после удара. Воспользуемся еще законом сохранения энергии для замкнутой системы из двух шаров, который будет иметь следующий вид:

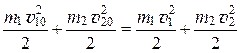. (2.20)

Отсюда находим:

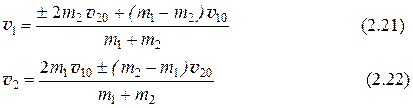
В этих выражениях знак "-" соответствует случаю шаров, движущихся навстречу друг другу, а знак "+" соответствует случаю, когда первый шар догоняет второй.

В случае абсолютно неупругого удара шары деформируются необратимо. После столкновения шары не восстанавливают свою форму и движутся дальше (или покоятся) вместе с одной и той же скоростью, образуя как бы единое целое. Закон сохранения импульса имеет вид

. (2.23)

Откуда можно найти общую скорость шаров после удара:

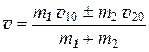. (2.24)

1.5. Элементы динамики вращательного движения твердого тела

При описании вращательного движения применяется идеализация - абсолютно твердое тело. При вращении все его точки описывают окружности, а центры этих окружностей лежат на одной прямой - оси вращения.

Если тело за время D t поворачивается на угол Dj, то угловая скорость определяет быстроту изменения угла поворота во времени:

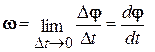. (3.1)

Направление вектора угловой скорости w определяется правилом правого винта: вектор w направлен так же, как направлен винт с правой резьбой при завинчивании, причем направление вращения винта совпадает с направлением вращения тела.

Изменение угловой скорости во времени характеризуется угловым ускорением:

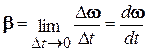. (3.2)

Если тело вращается вокруг неподвижной оси, то направления векторов w и b совпадают с направлением оси вращения.

Установим связь между линейными и угловыми характеристиками движения. При вращении твердого тела все угловые величины - Dj, w и b остаются неизменными для различных точек твердого тела, а линейные величины - скорость v и ускорение a - существенно зависят от расстояния R точек до оси вращения. Покажем это.

Действительно, при малых значениях интервала времени D t можно принять:

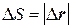. (3.3)

Как видно из рис.3-1, длина секущей D r равна:

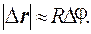
По определению:

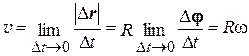, (3.4)

или в векторной форме:

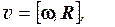(3.5)

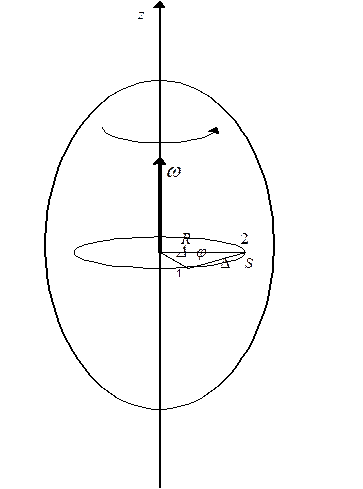
Рис. 3-1

Так как:

,

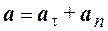где

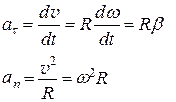(3.7)

Модуль полного ускорения:

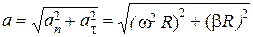. (3.8)

Таким образом, и нормальное и тангенциальное ускорения увеличиваются линейно с увеличением расстояния от точки до оси вращения.

Рассматривая вращение тела относительно неподвижной оси z, проходящей через центр масс, введем понятие момента силы относительно некоторой точки (относительно начала отсчета) (рис.3-2).

Рис.3-2

Сила F приложена в точке А, точка О - начало отсчета, т.е. точка, относительно которой определяется момент силы F, а r - радиус-вектор точки приложения силы. Момент силы определяется как векторное произведение радиуса-вектора r на саму силу F:

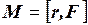. (3.9)

Вектор М перпендикулярен плоскости, в которой лежат векторы r и F, причем, если смотреть вдоль вектора М, то поворот от r к F по кратчайшему пути должен происходить по часовой стрелке (т.е. здесь также можно пользоваться правилом буравчика). Векторное произведение можно представить в виде определителя:

(3.10)

раскрывая который по элементам первой строки, можно получить выражение для момента. Модуль вектора М равен

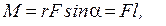(3.11)

где a - угол между направлением векторов r и F, а l - плечо силы, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.

Вращение твердого тела вызвано касательными силам F, т.е. силами, лежащими в плоскости, перпендикулярной оси вращения, и направленными по касательной к окружности в точках приложения сил (рис.3-4).

Проекция момента на ось Z представляет собой момент силы относительно оси Z:

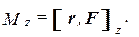(3.13)

Разложим вектор r на две составляющие - направленную вдоль оси Z (R _z) и перпендикулярно оси (R):

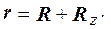
Тогда:

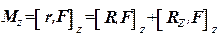. (3.14)

Рис. 3-4

Последний член этого выражения обращается в нуль, так как векторы R _z и F коллинеарны (т.е. направлены вдоль одной оси). Поэтому:

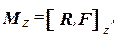(3.15)

т.е. проекция момента также направлена вдоль оси вращения.

Разобьем (мысленно) вращающееся твердое тело на множество N малых объемов. Понятие малый объем означает, что он настолько мал по сравнению с размерами тела, что его можно считать материальной точкой. Один из таких элементарных объемов массой m _i показан на рис. 3-5.

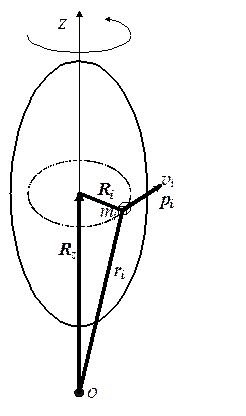
Рис. 3-5

Расстояние от этого элементарного объема до оси вращения равно R _i. Если тело вращается вокруг оси с угловой скоростью w, то i- й элементарный объем обладает линейной скоростью v _i, импульсом p_i = m _i p _i и моментом импульса относительно оси Z:

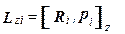(3.16)

Векторы R _i и p _i взаимно перпендикулярны и поэтому (3.16) можно переписать так:

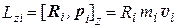. (3.17)

Подставив в (3.17) выражение для линейной скорости получим

(3.18)

где величина:

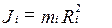(3.19)

называется моментом инерции материальной точки относительно оси вращения. Момент инерции определяет инерциальные свойства материальной точки при вращательном движении. Суммируя теперь (3.18) по всем элементарным объемам, на которые мы разбили тело, получим:

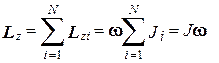, (3.20)

где величина:

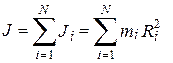(3.21)

называется моментом инерции твердого тела относительно оси Z. Строго говоря, момент инерции определяется не суммой, а интегралом, который представляет собой предел этой суммы:

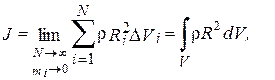(3.22)

где r - плотность материала, из которого состоит тело, а D V_i - элементарный объем. Таким образом, масса этого элементарного объема равна: m_i= rD V_i. Интегрирование ведется по всему объему тела.

Приведем выражения для моментов инерции некоторых тел.

Момент инерции круглого прямого цилиндра (рис. 3-6,а) относительно оси вращения, совпадающей с осью симметрии цилиндра. Выберем элемент объема в виде бесконечно тонкого цилиндра радиусом r, толщиной dr и высотой h. Тогда объем этого цилиндра будет равен dV=2prhdr. Подставив это выражение в (3.22), получим

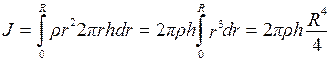. (3.23)

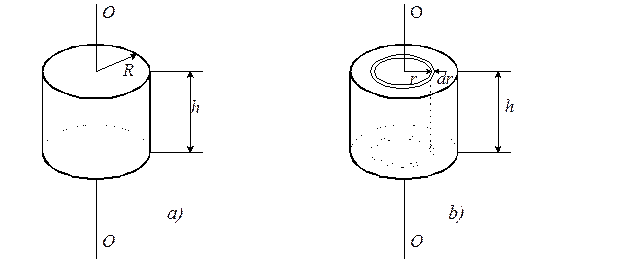Рис. 3-6

Цилиндр предполагается однородным, поэтому плотность r вынесена за знак интеграла. Поскольку масса цилиндра равна ,получим:

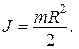(3.24)

Момент инерции круглого прямого кольцевого цилиндра (рис. 3-7), наружный радиус которого - R ₂, внутренний - R ₁,вычисляется аналогично, с той лишь разницей, что пределы интегрирования теперь будут соответственно равны R ₁ и R ₂.

Рис.3-7

Получим:

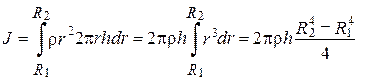. (3.25)

Поскольку масса цилиндра в этом случае равна

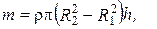(3.26)

получим окончательно

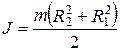. (3.27)

Момент инерции стержня длиной L и сечением S, относительно оси, относительно оси ОО^′ (рис. 3-8), проходящей через его середину.

Рис. 3-8

Выберем элементарный объем dV=Sdr в виде бесконечно короткого отрезка стержня dr, находящегося на расстоянии r от оси вращения. Из (3.22), получим

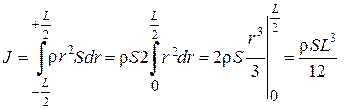. (3.28)

Учитывая, что масса стержня равна: m= r SL, получим

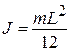. (3.29)

Момент инерции стержня, относительно оси, проходящей через один из его концов (рис.3-9), вычисляется так же, как и в предыдущем случае, но пределы интегрирования будут другими:

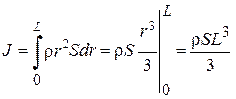. (3.30)

Поскольку масса стержня равна m= r SL, получим

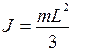(3.31)

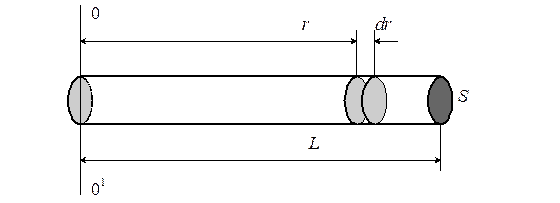
Рис. 3-9

Теорема Штейнера позволяет вычислить момент инерции тела относительно смещенной оси. Пусть, например, некоторое тело, изображенное на рис.3-10, обладает моментом инерции J ₀ относительно некоторой оси 0, проходящей через центр масс этого тела.

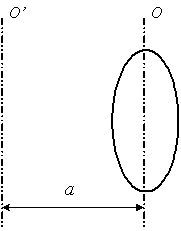
Рис. 3-10

Момент инерции того же тела, но относительно другой оси O’, смещенной относительно первой оси на расстояние а, будет выражаться формулой

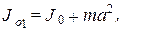(3.32)

где m - масса тела, а а - расстояние между осями.

Эту формулу легко проверить на примере двух последних случаев.

Стержень, изображенный на рис.3-8, имеет, согласно формуле (3.26), момент инерции, равный:

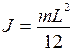
Например, стержень, изображенный на рис. 3-9, отличается от стержня, изображенного на рис. 3-8, тем, что ось его вращения смещена относительно прежней на расстояние

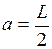
В соответствии с (3.28) получим для нового момента инерции:

.

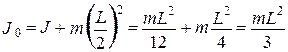Вернемся к рис. 3-5. Для i -го элемента, принадлежащего вращающемуся телу, второй закон Ньютона запишется в виде:

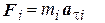(3.33)

Здесь:

F _i - касательная сила, действующая на элемент;

m_i - масса элемента;

a_{t i} - тангенциальное (касательное) ускорение:

(3.34)

где:

b - вектор углового ускорения тела;

R_i - расстояние от i -го элемента до оси вращения.

Таким образом:

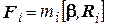. (3.35)

Момент этой силы получается в виде

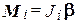. (3.36)

Суммируя теперь выражение моменты всех элементарных объемов, получим основное уравнение динамики вращательного движения:

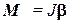, (3.37)

где J - момент инерции вращающегося тела, который определяется выражением (3.22).

По существу, это выражение является обобщением второго закона Ньютона на случай вращения тела. Важно подчеркнуть, что М - это суммарный момент всех внешних сил, действующих на тело.

Угловое ускорение тела представляет собой первую производную угловой скорости по времени. Поэтому:

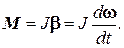
Поскольку момент инерции от времени не зависит, получим:

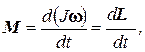
т.е.:

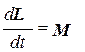. (3.38)

Выражение (3.38) представляет собой закон сохранения момента импульса твердого тела и является обобщением закона сохранения импульса (1.15) на случай вращательного движения. Моментом импульса твердого тела в выражении (3.38) называется величина:

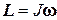. (3.39)

Если вращающееся тело изолировано, т.е. на него не действуют внешние силы, то и суммарный момент всех внешних сил также равен нулю. В этом случае мы получаем закон сохранения момента импульса для изолированного тела:

(3.40)

Для удобства запоминания основных соотношений, характеризующих поступательное и вращательное движение, а также для более глубокого понимания связей между этими видами движений можно воспользоваться следующей таблицей аналогий. Следует подчеркнуть, что эта таблица описывает формальные аналогии, однако связь между соотношениями не только формальная, а более глубокая - соотношения для вращательного движения являются обобщениями соотношений для поступательного движения.

Таблица аналогий

Поступательное движение Вращательное движение

1.Вектор перемещения 1. Угол поворота:

2. Линейная скорость: 2. Угловая скорость:

3. Линейное ускорение: 3. Угловое ускорение:

4. Внешняя сила: 4. Вращающий момент:

Дата добавления: 2014-01-07