Основные понятия. Помехозащищенные коды

Помехозащищенные коды

Лекция № 5

Помехозащищенными, или корректирующими, кодами называются коды, позволяющие обнаружить или обнаружить и исправить ошибки в кодовых комбинациях. Отсюда и деление этих кодов на две группы: коды с обнаружением ошибок и коды с обнаружением и исправлением ошибок.

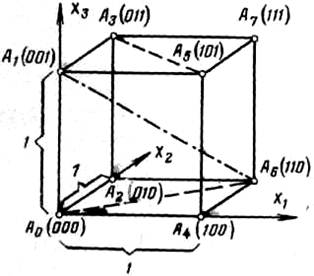Принципы обнаружения и исправления ошибок кодами хорошо иллюстрируются при помощи геометрических моделей. Любой n -элементный двоичный код можно представить с помощью n-мерного куба, в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояния между вершинами (кодовыми комбинациями) измеряется минимальным количеством ребер, находящихся между ними, обозначается буквой d и называется кодовым расстоянием.

Таким образом, кодовое расстояние – это то минимальное число элементов, в которых одна кодовая комбинация отличается от другой.

При n =1 n–мерный куб превращается в прямую длиной d=1, на одном конце которой располагается 1, а на другом 0. (n – число разрядов)

При n =2 имеем четыре возможные комбинации (N = 2² =4), которые располагаются на четырех вершинах квадрата. При этом комбинации 00 и 11, а также 10 и 01 отличаются друг от друга в двух разрядах, т.е. d = 2.

Кодовое расстояние между двумя комбинациями двоичного кода равно числу единиц, полученных при сложении этих комбинаций по модулю 2, например, 10 01 = 11 и 00 11 = 11. Такое определение кодового расстояния удобно при большой разрядности кодов. Так, складывая комбинации 10110101101

10000000010

мы определяем, что расстояние между ними d =7.

Для кода с n =3 восемь кодовых комбинаций размещаются на вершинах трехмерного куба. Этот куб строится так, что одна из его вершин лежит в начале координат. Каждой вершине куба приписывается кодовая комбинация по следующему правилу: на i -ом месте кодовой комбинации ставится 0, если проекция этой вершины на i -ую ось координат равна 0, и 1, если проекция равна 1. Например, мы хотим узнать, какую следует записать комбинацию в вершине А_6. Проектируя эту вершину на ось X₁, мы получим единицу.

На втором месте комбинации запишется также 1 (проекция на ось X ₂ равна единице). Т.к. проекция на ось X₃ равна нулю (проекция в начале координат), то на третьем месте комбинации запишется 0. Вся комбинация в точке А₆ – 110. Если использовать все восемь слов, то образуется двоичный код на все сочетания. Как было показано выше, такой код непомехоустойчив. Если же уменьшить число используемых комбинаций с 8 до 4,то появится возможность обнаружения одиночных ошибок. Для этого выберем только такие комбинации, которые отстоят друг от друга на расстоянии d= 2, например, А₀ А₆ А₃ А₅

000 110 011 101

Если будет принята комбинация 100, отстоящая от комбинации 000, 110 и 101 на расстоянии d =1, то очевидно, что при приеме такой комбинации произошла одиночная ошибка.

Представленные комбинации построены по определенному правилу, а именно содержат четное число единиц, а принятая комбинация 100-нечетное. Можно утверждать, что комбинация 100 образовалась при искажении одного разряда одной из разрешенных комбинаций, но определить, какая именно комбинация искажена, невозможно. Поэтому такие коды называются кодами с обнаружением ошибок.

Кроме указанной выше группы комбинаций, в кубе можно найти еще одну группу комбинаций с кодовым расстоянием d =2 А₇ А₁ А₂ А₄

(111 001 010 100)

В этих кодовых комбинациях нечетное число единиц и каждая из них может быть использована для обнаружения ошибки, возникшей при передаче, т.к. при одиночном искажении в комбинации будет четное число единиц. Однако если мы хотим получить код с обнаружением одиночной ошибки, то в передаче в передаче может участвовать только одна группа,т.е. четыре комбинации из возможных 8. В противном случае мы придем к непомехоустойчивому коду, в котором будут встречаться комбинации с d =1.

Таким образом, в помехозащищенных кодах есть комбинации разрешенные, составленные по определенному правилу и есть комбинации запрещенные, не соответствующие этому правилу. Так, если из восьми комбинаций трехразрядного кода мы образовали четыре комбинации, позволяющие обнаруживать одиночную ошибку (например, 111, 001, 010 и 100), то эти комбинации будут разрешенными, а остальные четыре (000, 011, 101, 110) являются запрещенными и должны фиксироваться на приеме как искаженные. Иногда совокупность разрешенных кодовых комбинаций, которые при заданных возможных искажениях не могут перейти друг в друга, называют системой непереходящих друг в друга сигналов.

Построение помехоустойчивого кода связано с недоиспользованием кодовых комбинаций, приводящим к так называемой избыточности. Избыточность означает, что из исходных символов можно построить больше комбинаций, чем их используется в данном коде. Если еще больше ограничить число разрешенных комбинаций, то можно создать код и с исправлением ошибок.

Выберем в трехмерном кубе такие вершины, кодовые обозначения которых отличались бы друг от друга на d =3. Такие вершины расположены на концах пространственных диагоналей куба. Их может быть только четыре пары: 000 и 111 или 001 и 110, или 100 и 011, или 010 и 101. Однако из этих четырех пар для передачи можно использовать только одну любую пару, т.к. использование большего числа пар приведет к тому, что в передаче будут использоваться комбинации, отличающиеся друг от друга на d <3.

Код, образованный по такому правилу и состоящий в данном случае из двух комбинаций, может исправить одиночную ошибку или обнаруживать две ошибки без возможности их исправления.

Пусть, например, передается код, состоящий из слов 001 и 110. На приеме получена комбинация 100. Сравнение ее с исходными комбинациями показывает, что от комбинации 110 она отличается в одном (втором) разряде, а от комбинации 001 в двух разрядах. Если считать, что сделана одна ошибка, то полученную комбинацию 100 следует исправить на 110.

От разрешенной комбинации 001 отличаются на d =1 комбинации 011, 000 и 101, а от комбинации 110 – комбинации 111,100 и 010. Они и являются своего рода комбинациями – спутниками, которые после приема можно относить к той или иной исходной комбинации.

Когда мы говорим об исправлении одиночной ошибки, то считаем, что вероятность двойной ошибки в канале связи пренебрежимо мала. Если такая вероятность достаточно велика, то код с d =3 можно использовать для обнаружения двойных ошибок, но при этом он уже исправлять одиночную ошибку не может. Действительно, если в нашем примере была принята комбинация 100,то уже нельзя утверждать, что была передана комбинация 110, т.к. при двойных ошибках это могла быть и искаженная комбинация 001.

Таким образом, дальнейшее повышение помехоустойчивости кода связано с увеличением кодового расстояния d, а это приводит к увеличению избыточности (вместо восьми комбинаций в нашем примере используются уже только две).

Корректирующая способность кода тесно связана с кодовым расстоянием:

а) при d =1 ошибка не обнаруживается;

б) при d =2 обнаруживаются одиночные ошибки;

в) при d =3 исправляются одиночные ошибки или обнаруживаются двойные.

В общем случае d=r+s+1, (3-5)

где d – минимальное кодовое расстояние;

r – число обнаруживаемых ошибок в слове;

s – число исправляемых ошибок в слове.

При этом обязательным условием является 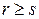. Если r=s, то код обнаруживает 2 x или исправляет x ошибок. Так в нашем примере d= 3, и если r=s =1, то код может обнаружить одну ошибку и исправить ее, т.е. x= 1. Если r= 2, s= 0, то код может обнаружить только две ошибки. Как следует из уравнения (3-5), для того чтобы код мог исправить одну ошибку и обнаружить две, необходимо, чтобы d= 2+1+1=4. При том же d= 4 может быть и вариант, когда r= 3, s= 0. Если d= 5, то могут быть уже три варианта: r= s= 2; r= 3, s= 1; r= 4, s= 0.

Если код только обнаруживает ошибки, то d=r+1, т.е. r=d - 1 (3-6)

Если код только исправляет ошибки, то d= 2 s+ 1, т.е. (3-7)

Итак, использование геометрических моделей позволяет просто строить малоразрядные корректирующие коды. Однако при длине кода n > 3 трудно уже воспользоваться геометрической моделью, т.к. такая модель должна быть многомерной. Если еще для n =4 можно вычертить четырехмерный “куб”, так называемый гиперкуб, то для n >4 это практически сделать невозможно. Поэтому для построения многоразрядных помехоустойчивых кодов используются различные правила и методики, к рассмотрению которых мы и перейдем.

Дата добавления: 2014-01-07