Выбор математической модели

Уже отмечалось, что под моделью понимается вид функции отклика Y=F(x₁, x₂,..., x_n). Выбрать модель, это значит выбрать вид этой функции, и записать ее уравнение. Тогда остается так спланировать эксперимент и провести его, чтобы можно было оценить численные значения констант (коэффициентов) этого уравнения.

Рассмотрим принципы выбора моделей на геометрической интерпретации уравнения на примере двухфакторного эксперимента.

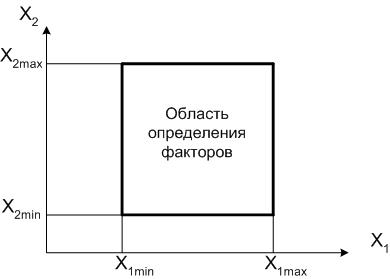
Рис. 3. Область определения факторов

Чтобы указать на области определения факторов параметр оптимизации, требуется еще одна ось координат. Если построить ее нормально к плоскости определения факторов, то поверхность параметра оптимизации будет выглядеть следующим образом (рис.4).

Пространство, на котором строится поверхность параметра оптимизации носит название факторного пространства. Если провести сечение поверхности параметра оптимизации плоскостями, параллельными плоскости OX₁X₂, и полученные кривые спроецировать на факторное пространство, мы будем иметь графическое изображение изолиний – линий равных значений параметра оптимизации.

Точка М – точка с максимальными значениями параметра оптимизации.

После этого отступления можно вернуться к вопросу: как спланировать эксперимент, чтобы найти экстремум параметра оптимизации при минимуме затрат?

Если бы мы имели таблицу всех возможных состояний объекта и соответствующих им параметров оптимизации, то необходимости в математической модели не было бы, мы бы просто выбрали значения факторов, соответствующих экстремуму параметра оптимизации. Но эта ситуация нереальна из-за сложности объекта исследования.

Другой алгоритм решения задачи заключается в том, чтобы осуществить выбор некоторого числа состояний объекта и определить экспериментально в них значения параметра оптимизации с последующим построением математической модели, используемой далее для предсказания результатов

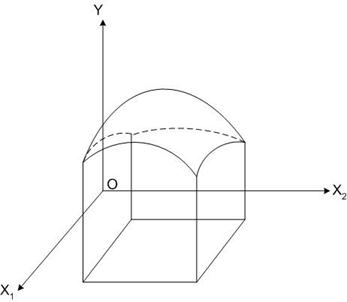
Рис. 4. Область определения параметра оптимизации

Этот метод получил название шагового принципа поиска экстремума.

В основе реализации шагового принципа поиска оптимального решения задачи находятся следующие предположения.

1. Поверхность параметра оптимизации непрерывна.

2. Поверхность параметра оптимизации имеет единственный оптимум (что соответствует монотонности функции).

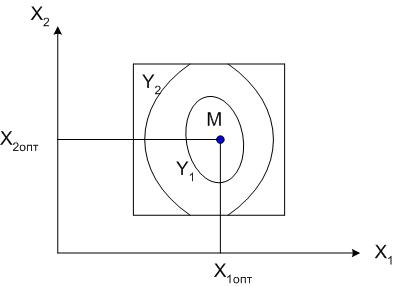
Рис. 5. Линии равных значений параметра оптимизации

Эти предположения позволяют представить функцию в виде степенного ряда в окрестностях любой точки факторного пространства. Если мы знаем значение параметра оптимизации в нескольких соседних точках, то сможем (в силу непрерывности и гладкости функции) предсказать значение параметра оптимизации в любой точке. Следовательно, можно найти точку на факторном пространстве, для которой значение параметра оптимизации экстремально. Отсюда ясно, что следующий эксперимент следует переносить именно в эту точку, двигаясь в одном направлении и пренебрегая другими. Рано или поздно, реализуя шаговый принцип, мы уткнемся в оптимум.

Дата добавления: 2014-01-07