Алгоритм метода Розенкранца

Другой способ преобразования КС-грамматики к нормальной форме Грейбах (Метод Розенкранца)

Рассмотрим другой способ построения грамматики, в которой каждое правило имеет вид , где 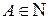, , 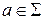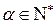. Здесь грамматика переписывается только один раз. Пусть 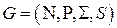- КС-грамматика, в которой нет пустых правил (даже вида 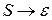) и цепных правил.

Определение: Пусть 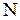и 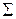- два непересекающихся алфавита. Системой определяющих уравнений в алфавитах , называется система уравнений вида

, (1)

где

, , .

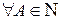Если 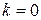, то уравнение записывается .

Определение: Решением системы (1) называется отображение вида , и это отображение называется наименьшей неподвижной точкой системы определяющих уравнений.

Определение: Матричная форма записи системы уравнений выглядит следующим образом

, (2)

где

-вектор строка;

- матрица порядка 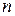(квадратная матрица);

-вектор строка.

Причем , (3)

где

.

Если во множестве правил для 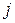-го нетерминала существуют правила вида

,

где

, ,

то выполняется условие (3), иначе, если таких правил нет, то .

Рассматриваем множество правил для 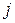-го нетерминала, которые начинаются с 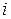-го нетерминала.

Если существуют правила вида

,

тогда

.

Если множество правил для данного нетерминала пусто, то .

.

Построим для системы (1) эквивалентную систему определяющих уравнений.

Лемма: Пусть система (1) – система определяющих уравнений, тогда наименьшей неподвижной точкой данной системы будет выражение вида

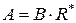, (4)

где

;

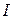- единичная матрица, на главной диагонали которой находятся 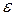, все остальные элементы данной матрицы – пустые выражения.

Если положить

,

то наименьшую неподвижную точку матричного уравнения

можно записать в виде

.

К сожалению, для данной системы нельзя найти соответствующую грамматику: она не является системой определяющих уравнений, так как элементы матрицы могут буть бесконечными суммами членов исходных уравнений. Однако можно заменить новой матрицей «неизвестных» 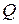, каждый элемент которой, расположенный в 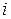-й строке и 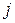-м столбце, - новый символ.

Тогда, заметив, что

,

можно получить систему определяющих уравнений

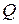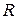с неизвестными . Отметим, что если матрицы и - матрицы порядка 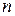, то система состоит из 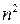уравнений.

Лемма: Пусть система – система определяющих уравнений в алфавитах 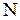и 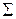и пусть матрица 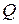- матрица того же порядка что и 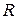. Причем, все её элементы –различные новые символы, тогда система определяющих уравнений вида

имеет наименьшую неподвижную точку, которая совпадает с наименьшей неподвижной точкой системы .

Вход: Приведенная КС-грамматика без правил вида .

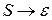Выход: КС-грамматика в нормальной форме Грейбах.

Метод:

1. Строим систему определяющих уравнений вида

;

2. Строим эквивалентную систему определяющих уравнений вида

и соответствующую ей грамматику 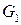. Так как, в вектор-строке 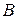каждая непустая компонента начинается терминалом, то в силу приведенности грамматики 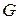все правые части правил для нетерминала 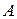грамматики 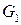будут начинаться с терминала;

3. В силу того, что в грамматике 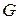отсутствуют пустые правила, то есть 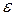не является элементом матрицы 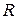, поэтому для каждого элемента матрицы 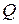все соответствующие правила будут начинаться с символов из . В тех правых частях правил если на первом месте находится нетерминал из 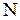, то заменяем его на соответствующие правые части для данного нетерминала правил. В результате получится грамматика, у которой правые части всех правил начинаются с терминала;

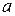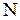4. Если в правых частях правил терминал находится не на первом месте, то заменяем его на новый нетерминал , который добавляем , и во множество правил добавляем правило вида

.

Результирующую грамматику обозначить через .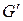

Пример:

.

Решение:

1. Строим систему определяющих уравнений

,

где

;

;

2. Строим эквивалентную систему определяющих уравнений

,

где

;

;

;

;

;

;

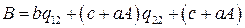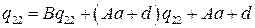Строим грамматику с правилами

,

,

,

,

,

;

3. Заметим, что символ - бесполезный символ.

4. Делаем замену всех нетерминалов стоящих на первом месте в матрице 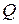на соответствующие правые части правил. В результате получаем грамматику с правилами вида

,

,

,

,

,

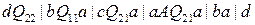
Домашнее задание: Привести к нелеворекурсивному виду грамматику

.

И привести к нормальной форме Грейбах первым и вторым способом.

Дата добавления: 2014-01-07