
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Система двух случайных величин
1) 9,44; 2) 10,12; 3) 10, 56; 4) 11,08.
Минус бесконечности; 2) нулю; 3) единице; 4) бесконечности.
1) -3; 2) -1; 3) -0,5; 4) 0.
53.
Плотность распределения; 2) центральный момент первого порядка; 3) нормальная функция распределения.
Тесты
51. Как для непрерывной случайной величины называется функция, являющаяся производной функции распределения этой случайной величины?
52. Случайная величина, обладающая распределением Паскаля является:
1) дискретной; 2) непрерывной; 3) распределённой.

54. По какой формуле можно вычислить вероятность попадания значения случайной величины с функцией распределения F (x) на интервал (a, b)?
1) F (b - a); 2) F (a) + F (b); 3) F (b) - F (a); 4) F (a) - F (b).
55. Чему равно значение функции распределения случайной величины на минус бесконечности?
56. Случайная величина, обладающая показательным распределением является:
1) непрерывной; 2) дискретной; 3) распределённой; 4) постоянной.
57. Средняя дальность полета снарядов в учебных стрельбах равна 2000 метров. Предполагая, что дальность полёта распределена по нормальному закону со средним квадратическим отклонением 40 метров, найти процент снарядов улетевших на расстояние более 2050 метров?
Лекция 7
До сих пор рассматривалась одна случайная величина X. Но на практике часто имеют дело сразу с несколькими случайными величинами. Интересен, конечно, случай, когда есть вероятностная (стохастическая) зависимость их друг от друга. Тогда можно говорить о законе совместного распределения случайных величин.
Пример 1. Кирпичи формируют из кусков глины одинаковой массы М, но длина X, ширина Y и высота Z каждого из них случайны. Эти величины не могут быть совершенно произвольными, т.к. между ними должно соблюдаться соотношение: r × X × Y × Z = М, где r - плотность глины.
Пример 2. Обследуется группа людей: измеряются их рост X и вес Y. Эти случайные величины, конечно же, не будут независимыми: как правило, чем больше X, тем больше Y.
Пример 3. Количество выкуренных сигарет и число прожитых лет.
Закон распределения двумерной дискретной случайной величины можно задать таблично. Например, в таком виде
| Y | X | ||
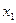 =2 =2
| 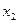 =5 =5
| 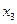 =7 =7
| |
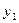 =3 =3
| 0,25 | 0,15 | 0,20 |
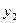 =6 =6
| 0,15 | 0,10 | 0,15 |
Здесь, к примеру, число 0,20 – это вероятность паре случайных величин (X, Y) принять значения (7, 3). Сумма стоящих во всех клетках вероятностей, конечно, должна быть равна 1.
Количественной мерой взаимосвязи двух случайных величин является ковариация (корреляционный момент, корреляционная функция, второй смешанный центральный момент), равная математическому ожиданию произведения отклонений случайных величин X и Y от своих математических ожиданий:
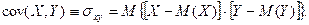
Используя свойства математического ожидания, можно вывести более удобную для вычислений формулу ковариации:
cov (X, Y) = M (X × Y) – M (X) × M (Y).
Если поделить ковариацию на произведение средних квадратических отклонений случайных величин X и Y, то получим коэффициент корреляции
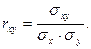 (11)
(11)
З а д а ч а. Для приведённого выше закона распределения найти коэффициент корреляции.
Решение. Математическое ожидание произведения X × Y равно М (X, Y) =
= 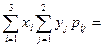 2×(3×0,25+6×0,15)+5×(3×0,15+6×0,1)+7×(3×0,2+6×0,15) = 19,05.
2×(3×0,25+6×0,15)+5×(3×0,15+6×0,1)+7×(3×0,2+6×0,15) = 19,05.
Вероятности значений X и Y будут такими: Р (X = 2) = 0,25 + 0,15 = 0,4; Р (X = 5) = 0,15 + 0,1 = 0,25; Р (X = 7) = 0,2 + 0,15 = 0,35; Р (Y = 3) = 0,25 + 0,15 + 0,2 = 0,6; Р (Y = 6) = 0,15 + 0,1 + 0,15 = 0,4. Следовательно, математические ожидания получатся равными: М (X) = 2 × 0,4 + 5 × 0,25 + 7 × 0,35 = 4,5; М (Y) = 3 × 0,6 + 6 × 0,4 = 4,2. Дисперсия D (X) = 4 × 0,4 + 25 × 0,25 + 49 × 0,35 - 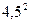 = 4,75, а D (Y) = 9 × 0,6 + 36 × 0,4 -
= 4,75, а D (Y) = 9 × 0,6 + 36 × 0,4 - 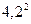 = 2,16. Средние квадратические отклонения равны
= 2,16. Средние квадратические отклонения равны 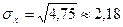 и
и 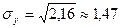 . Теперь по формуле (11) находим коэффициент корреляции:
. Теперь по формуле (11) находим коэффициент корреляции:
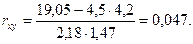
Близкое к нулю значение коэффициента корреляции говорит о слабой взаимозависимости заданных выбранным законом распределения случайных величин.
Вообще же, абсолютная величина коэффициента корреляции в любом случае не может превышать единицу: 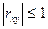 . Если случайные величины независимы, то их коэффициент корреляции равен нулю. Однако в обратную сторону это утверждение не действует: если коэффициент корреляции равен нулю, то случайные величины могут быть зависимыми и даже связаны между собой функционально (но не линейно). Если он отличен от нуля, то говорят о коррелированности случайных величин, т.е. о вероятностной (не строго функциональной) зависимости величин, которая возникает, когда одна из величин зависит не только от второй, но и других факторов, или когда их изменения обусловлены одними и теми же условиями. Если коэффициент корреляции близок по модулю к 1, то взаимозависимость величин сильная (например, уровень заработной платы и качество потребляемых продуктов питания). Если он отрицателен, то говорят об антикорреляции (например, количество выкуренных сигарет и продолжительность жизни).
. Если случайные величины независимы, то их коэффициент корреляции равен нулю. Однако в обратную сторону это утверждение не действует: если коэффициент корреляции равен нулю, то случайные величины могут быть зависимыми и даже связаны между собой функционально (но не линейно). Если он отличен от нуля, то говорят о коррелированности случайных величин, т.е. о вероятностной (не строго функциональной) зависимости величин, которая возникает, когда одна из величин зависит не только от второй, но и других факторов, или когда их изменения обусловлены одними и теми же условиями. Если коэффициент корреляции близок по модулю к 1, то взаимозависимость величин сильная (например, уровень заработной платы и качество потребляемых продуктов питания). Если он отрицателен, то говорят об антикорреляции (например, количество выкуренных сигарет и продолжительность жизни).
З а д а ч а. Даны законы распределения двух независимых случайных дискретных величин Х и Y:
| Y | -1 | |
| р | 0,2 | 0,3 |
| Х | -1 | |
| р | 0,3 | 0,7 |
Найти закон распределения случайной величины Z = 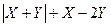 , математическое ожидание М (Z), дисперсию D (Z), среднее квадратическое отклонение s и вероятность р попадания значений Z в интервал (M - s, M + s).
, математическое ожидание М (Z), дисперсию D (Z), среднее квадратическое отклонение s и вероятность р попадания значений Z в интервал (M - s, M + s).
Решение. Сначала посчитаем, какие значения может принимать величина Z и каковы вероятности этих значений с учетом независимости X и Y. Для этого нужно перебрать все возможные комбинации (X, Y):
1) (-1, -1): Z = 3, 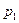 = Р (X × Y) = Р (X = -1) × Р (Y = -1) = 0,3 × 0,2 = 0,06;
= Р (X × Y) = Р (X = -1) × Р (Y = -1) = 0,3 × 0,2 = 0,06;
2) (-1, 0): Z = 0, 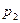 = 0,3 × 0,3 = 0,09;
= 0,3 × 0,3 = 0,09;
3) (-1, 1): Z = -3, 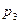 = 0,3 × 0,5 = 0,15;
= 0,3 × 0,5 = 0,15;
4) (2, -1): Z = 5, 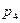 = 0,7 × 0,2 = 0,14;
= 0,7 × 0,2 = 0,14;
5) (2, 0): Z = 4, 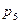 = 0,7 × 0,3 = 0,21;
= 0,7 × 0,3 = 0,21;
6) (2, 1): Z = 3, 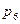 = 0,7 × 0,5 = 0,35.
= 0,7 × 0,5 = 0,35.
Все значения Z встречаются по одному разу, кроме Z = 3, для которого вероятности надо сложить 0,06 + 0,35 = 0,41. В результате получаем закон распределения случайной величины Z:
| Z | -3 | ||||
| p | 0,15 | 0,09 | 0,41 | 0,21 | 0,14 |
Складывая теперь произведения, найдём математическое ожидание М (Z) = -3 × 0,15 + 0 × 0,09 + 3 × 0,41 + 4 × 0,21 + 5 × 0,14 = 2,32. Дисперсия равна D (Z) = 9 × 0,15 + 0 × 0,09 + 9 × 0,41 + 16 × 0,21 + 25 × 0,14 - 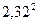 » 6,52. Среднее квадратическое отклонение s =
» 6,52. Среднее квадратическое отклонение s = 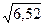 » 2,55. Интервал значений (М - s, М + s), следовательно, будет таким: (-0,23; 4,87), а значит, в него попадут три значения Z (0, 3, 4). Суммируя три соответствующие вероятности, получим Р = 0,71.
» 2,55. Интервал значений (М - s, М + s), следовательно, будет таким: (-0,23; 4,87), а значит, в него попадут три значения Z (0, 3, 4). Суммируя три соответствующие вероятности, получим Р = 0,71.
Лекция 8
|
|
Дата добавления: 2014-01-07; Просмотров: 2174; Нарушение авторских прав?; Мы поможем в написании вашей работы!