
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение знакопеременного ряда. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов
|
|
|
|
Ряды с положительными членами. Достаточные признаки сходимости положительных рядов (принцип сравнения, радикальный признак Коши, признак Даламбера). Интегральный признак Коши-Маклорена.
Определение. Ряд 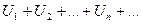 называется положительным, если все его члены неотрицательны:
называется положительным, если все его члены неотрицательны: 
Теорема (критерий сходимости положительных рядов).
Для того, чтобы положительный ряд сходился, необходимо и достаточно, чтобы последовательность частных сумм ряда была ограничена (критерий носит теоретическое значение, и является основой, на которой базируются
другие признаки).
Достаточные признаки сходимости положительных рядов.
Признаки сравнения.
Теорема 1. Пусть члены положительных рядов  (1) и
(1) и 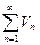 (2) с вязаны соотношением
(2) с вязаны соотношением  , тогда из сходимости ряда (2) (большего) следует сходимость ряда (1) (меньшего); если ряд (1) (с меньшими членами) расходится, то расходится ряд (2) (с большими членами).
, тогда из сходимости ряда (2) (большего) следует сходимость ряда (1) (меньшего); если ряд (1) (с меньшими членами) расходится, то расходится ряд (2) (с большими членами).
Теорема 2. Если предел отношения общих членов положительных рядов (1) и (2) есть конечное не равное нулю число 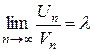 , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
Примечание. В качестве рядов сравнения используют эталонные ряды, о поведении которых известно:
1) ряд, составленный из членов геометрической прогрессии 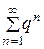 , который сходится
, который сходится  , и расходится при
, и расходится при  ;
;
2) обобщённый гармонический ряд 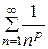 с показателем сходимости р, который сходится при
с показателем сходимости р, который сходится при 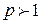 , и расходится при
, и расходится при 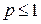 .
.
Выбор одного из двух эталонных рядов для исследования неизвестного ряда определяется по виду исследуемого ряда.
Пример 1. Исследовать сходимость ряда 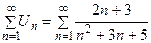 .
.
Сравним исследуемый ряд  с рядом
с рядом  , который расходится. Найдём
, который расходится. Найдём  , следовательно исходный ряд
, следовательно исходный ряд  расходится (на основании предельного признака сравнения).
расходится (на основании предельного признака сравнения).
Пример 2. Исследовать ряд 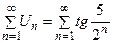 .
.
|
|
|
Сравним исследуемый ряд  с рядом
с рядом 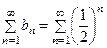 , который сходится. Определим
, который сходится. Определим  , исходный ряд сходится, так как сходится ряд сравнения.
, исходный ряд сходится, так как сходится ряд сравнения.
Признак Даламбера.
Пусть для положительного ряда 
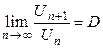 , тогда при
, тогда при 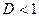 ряд сходится, при D >1 ряд расходится.
ряд сходится, при D >1 ряд расходится.
Замечание. При D =1 вопрос о сходимости ряда остается открытым.
Радикальный признак Коши.
Пусть для положительного ряда  ,
,  , тогда при k<1 ряд сходится, а при k >1 ряд расходится.
, тогда при k<1 ряд сходится, а при k >1 ряд расходится.
Замечание. При k =1 вопрос о сходимости ряда остается открытым.
Теорема (интегральный признак Коши-Маклорена).
Пусть функция 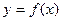 удовлетворяет условиям: 1) определена и непрерывна на
удовлетворяет условиям: 1) определена и непрерывна на  ; 2)
; 2) 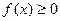 ; 3) монотонно убывает; 4)
; 3) монотонно убывает; 4) 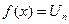 . Тогда если несобственный интеграл
. Тогда если несобственный интеграл 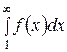 сходится, то сходится ряд
сходится, то сходится ряд  ; а если несобственный интеграл
; а если несобственный интеграл 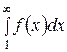 расходится, то расходится ряд
расходится, то расходится ряд  .
.
Пример. Исследовать сходимость гармонического ряда 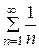 .
.
Так как  , ТО
, ТО 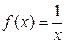 И
И 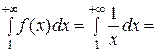
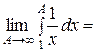

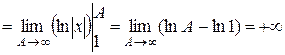 . Несобственный интеграл расходится, поэтому гармонический ряд расходится.
. Несобственный интеграл расходится, поэтому гармонический ряд расходится.
Рассмотрим ряды с членами произвольного знака, иначе знакопеременные ряды. Среди них часто встречаются ряды, члены которых имеют чередующиеся знаки.
Определение. Числовой ряд называется знакопеременным, если среди его членов встречаются как положительные, так и отрицательные.
Пример. 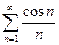 .
.
Определение. Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки. 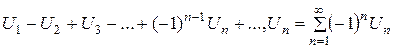 , где
, где 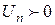 (3)
(3)
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и общий член ряда стремится к нулю, то ряд сходится и его сумма не превосходит первого члена ряда.
Любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак.
Пример. Доказать сходимость ряда 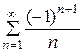 . Сколько членов ряда нужно взять, чтобы вычислить сумму с точностью 0,1.
. Сколько членов ряда нужно взять, чтобы вычислить сумму с точностью 0,1.
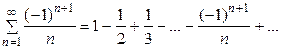 – сходится по признаку Лейбница, так как члены ряда убывают по абсолютной величине и общий член ряда
– сходится по признаку Лейбница, так как члены ряда убывают по абсолютной величине и общий член ряда  стремится к нулю при
стремится к нулю при 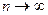 . Для вычисления суммы ряда с точностью 0,1 воспользуемся оценкой остатка
. Для вычисления суммы ряда с точностью 0,1 воспользуемся оценкой остатка 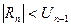 , то есть
, то есть  . Таким образом достаточно, чтобы выполнялось неравенство
. Таким образом достаточно, чтобы выполнялось неравенство  . Для нахождения суммы ряда с заданной точностью необходимо сложить девять первых членов.
. Для нахождения суммы ряда с заданной точностью необходимо сложить девять первых членов.
|
|
|
Пусть  (4) – знакопеременный ряд. Рассмотрим ряд, составленный из модулей членов ряда (4), то есть
(4) – знакопеременный ряд. Рассмотрим ряд, составленный из модулей членов ряда (4), то есть  (5).
(5).
Определение. Сходящийся ряд (4) называется абсолютно сходящимся, если сходится ряд (5), составленный из модулей членов ряда (4).
Определение. Сходящийся ряд (4) называется условно сходящимся, если ряд (5) расходится.
Теорема. Если ряд (5) сходится, то ряд (4) сходится. (абсолютная сходимость влечет за собой обычную сходимость/расходимость).
Примеры. Исследовать сходимость рядов.
1) 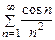 . Составим ряд из модулей
. Составим ряд из модулей  ,
,  . Ряд
. Ряд  сходится, ряд
сходится, ряд 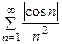 сходится, и потому ряд
сходится, и потому ряд  сходится абсолютно.
сходится абсолютно.
2) 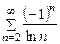 . Ряд из модулей
. Ряд из модулей 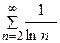 расходится, так как
расходится, так как 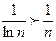 и ряд
и ряд 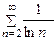 расходится. Исследуемый ряд
расходится. Исследуемый ряд  сходится по признаку Лейбница. Этот ряд сходится условно.
сходится по признаку Лейбница. Этот ряд сходится условно.
3)  . Ряд из модулей
. Ряд из модулей  расходится, так как общий член ряда не стремится к нулю:
расходится, так как общий член ряда не стремится к нулю: 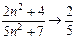 при
при  . Исследуемый ряд расходится.
. Исследуемый ряд расходится.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1008; Нарушение авторских прав?; Мы поможем в написании вашей работы!