Статистические оценки параметров распределения

Элементы математической статистики.

Основная задача математической статистики состоит в получении выводов о массовых явлениях и процессах, по данным наблюдений над ними или экспериментов. Эти статистические выводы относятся не к отдельным испытаниям, а представляют собой утверждения об общих характеристиках этого явления (вероятностях, законах распределения и их параметрах, математических ожиданиях, дисперсиях и т. д.) в предположении постоянства условий, порождающих исследуемое явление.

Математическая статистика опирается на теорию вероятностей, и её цель - оценить характеристики генеральной совокупности по выборочным данным.

Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов.

Генеральной совокупностью называется совокупность объектов, из которых производится выборка.

Объёмом совокупности (выборочной или генеральной) называется число объектов этой совокупности.

При составлении выборки можно поступать двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращён или не возвращён в генеральную совокупность. Соответственно выборки разделяют на повторные и бесповторные.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы выборка правильно представляла пропорции генеральной совокупности. Это требование кратко формулируют так: выборка должна быть репрезентативной (представительной).

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществлять случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.

Способы отбора.

Принципиально делятся на два вида:

1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся:

а) простой случайный бесповторный отбор;

б) простой случайный повторный отбор (объекты извлекают по одному из всей генеральной совокупности).

2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:

а) типический отбор (Объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, а из продукции каждого станка в отдельности. Типическим отбором пользуются тогда, когда исследуемый признак заметно колеблется в различных типических частях генеральной совокупности);

б) механический отбор (Генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают по одному объекту. Например, если надо отобрать 20% деталей, то отдирают каждую 5-ю деталь. Иногда механический отбор может не обеспечивать репрезентативность выборки. Например, если отбирают каждую 20-ю обтачиваемую деталь, а после отбора производят замену резца, то отобранными окажутся все летали, обточенные затупленным резцом);

в) серийный отбор (Объекты отбирают из генеральной совокупности не по одному, а сериями, которые подвергаются сплошному обследованию. Используется тогда, когда исследуемый признак колеблется в различных сериях незначительно).

На практике часто применяют комбинированный отбор. Например, иногда разбивают генеральную совокупность на серии одинакового объёма, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.

Статистическое распределение выборки.

Пусть из генеральной совокупности извлечена выборка, причём значение признака x₁ наблюдается n₁ раз, признака x₂ наблюдается n₂ раз, …, признака x_к - n_к раз.

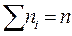- объем выборки.

Наблюдаемые значения x_i называются вариантами. Последовательность x_i в возрастающем порядке называется вариационным рядом.

Числа наблюдений n_i называются частотами, а их отношения к объёму выборки 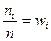называются относительными частотами.

Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение также можно задать в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Пример: задано распределение частот выборки:

xi
ni

Написать распределение относительных частот.

Решение:

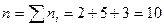- объём выборки.

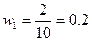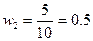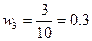; ; - относительные частоты.

Распределение относительных частот:

xi
wi	0.2	0.5	0.3

Контроль: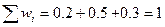

Полигон и гистограмма.

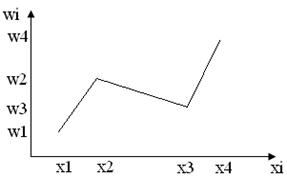
Полигон частот – это ломаная, отрезки которой соединяют точки (x_i, n_i).

Полигон относительных частот – это ломаная, отрезки которой соединяют точки (x_i, w_i).

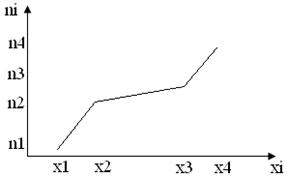
В случае непрерывного признака строят гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинны h и для каждого частичного интервала находят n_i - сумму частот вариант, попавших в i-ый интервал.

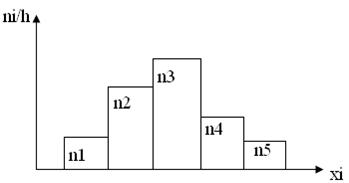Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длинной h, а высоты равны отношению 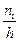- плотность частоты.

Площадь i-го частичного прямоугольника равна n_i –сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объёму выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длинной h, а высоты равны - плотность относительной частоты.

Площадь гистограммы относительных частот равна 1.

Эмпирическая функция распределения.

Пусть известно статистическое распределение частот количественного признака X. Введём обозначения: n_x – число наблюдений, при которых наблюдалось значение признака, меньшее x; n – общее число наблюдений (объём выборки). Ясно, что относительная частота события {X<x} равна 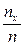. Если x изменяется, то изменяется и относительная частота, т. е. относительная частота 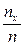есть функция от x. Так как эта функция находится эмпирическим (опытным) путём, то её называют эмпирической.

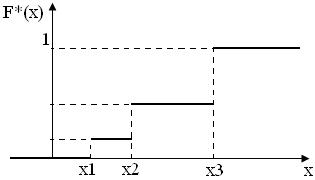
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F^*(x), определяющую для каждого значения x относительную частоту события X<x:

,

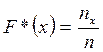где n_x – число вариант, меньших x; n – объём выборки.

В отличие от эмпирической функции распределения выборки, функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между ними состоит в том, что теоретическая функция распределения F(x) определяет вероятность события X<x, а эмпирическая функция F^*(x) – относительную частоту этого события. Из теоремы Бернулли следует, что относительная частота события X<x, т. е. F^*(x) стремиться по вероятности к вероятности F(x) этого события. Другими словами, при больших n числа F^*(x) и F(x) мало отличаются друг от друга. Поэтому F^*(x) используют для приближённого вычисления F(x).

F^*(x) обладает всеми свойствами F(x):

1. F^*(x) 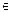[0, 1];

2. F^*(x) – неубывающая функция;

3. если x₁ - наименьшая варианта, то F^*(x)=0 при x ≤ x₁;

если x_k – наибольшая варианта, то F^*(x)=1 при x > x_k.

Статистические оценки параметров распределения.

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно, возникает задача оценки параметров, которыми определяется это распределение (нормальное распределение – а и 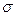, распределение Пуассона - ).

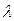Обычно в распоряжении исследователя имеются лишь данные выборки, например, значения количественного признака x₁, x₂, …, x_n, полученные в результате n наблюдений.

Через эти данные и выражают оцениваемый параметр. Рассматривая x₁, x₂, …, x_n как независимые случайные величины x₁, x₂, …, x_n, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая и даёт приближённое значение оцениваемого параметра.

Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определённым требованиям.

Пусть Q^* - статистическая оценка неизвестного параметра Q теоретического распределения.

Несмещённой называют статистическую оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объёме выборки, т. е.

M (Q^* ) = Q.

Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объёме выборки) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объёма (n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при 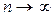стремится по вероятности к оцениваемому параметру.

Генеральная средняя.

Генеральной средней 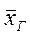называется среднее арифметическое значений признака генеральной совокупности

.

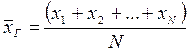Если значения признака x₁, x₂, …, x_к имеют соответственно частоты N₁, N₂, …, N_k, то

.

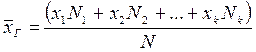Выборочной средней 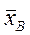называют среднее арифметическое значений признака выборочной совокупности

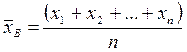или .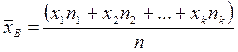

В качестве оценки 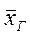принимают .

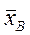Убедимся, что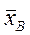- несмещённая оценка, т. е. покажем, что математическое ожидание этой оценки равно 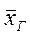. Будем рассматривать 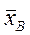как случайную величину и x₁, x₂, …, x_n – как независимые, одинаково распределённые случайные величины x₁, x₂, …, x_n. Поскольку эти величины одинаково распределены, то они имеют одинаковые числовые характеристики, в частности, одинаковые математические ожидания. А так как математическое ожидание среднего арифметического одинаково распределенных случайных величин равно математическому ожиданию каждой из величин, то . (*)

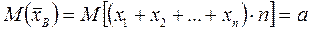Приняв во внимание, что каждая из величин x₁, x₂, …, x_n имеет то же распределение, что и генеральная совокупность, заключаем, что числовые характеристики этих величин и генеральной совокупности одинаковы. В частности, математическое ожидание a каждой из величин равно математическому ожиданию признака x генеральной совокупности, т. е. .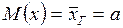

Заменив в (*) математическое ожидание a на 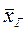, окончательно получим .

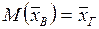Можно показать, что 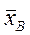является состоятельной оценкой .

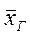Генеральной дисперсией D_Г называется среднее арифметическое квадратов отклонения значений признака генеральной совокупности от их среднего значения :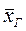

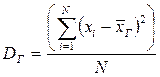или .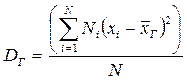

Выборочной дисперсией D_В называется среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :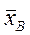

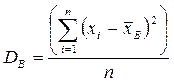или .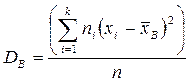

Формула для вычисления дисперсии.

Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:

.

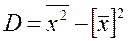Доказательство:

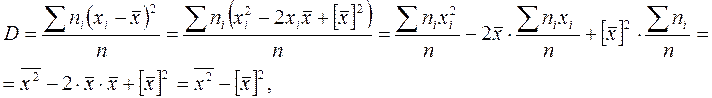
где ; .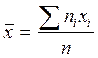

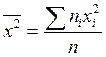D_В является смещённой оценкой D_Г.

Можно показать, что .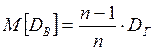

Легко «исправить» D_В так, чтобы её математическое ожидание было равно D_Г. Достаточно для этого умножить D_В на (n-1)/n. Получаем исправленную выборочную дисперсию:

.

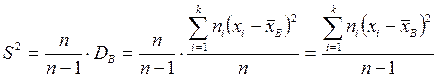S² является несмещённой оценкой D_Г.

Действительно, .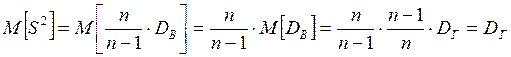

Итак, в качестве оценки D_Г принимают исправленную выборочную дисперсию:

,

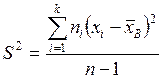где S – исправленное среднеквадратическое отклонение.

Дата добавления: 2014-01-07