
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Несобственный интеграл по бесконечному промежутку
|
|
|
|
Просматривая математические тексты, нетрудно наткнуться на выражения вида 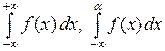 или
или 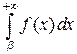 . С точки зрения введенного нами понятия интеграла Римана по отрезку приведенные интегральные выражения представляются бессмыслицей. Действительно, мы не сможем составить ни одной интегральной суммы, так как никогда не кончим разбивать бесконечный промежуток на конечные отрезки и выбирать на них отмеченные точки. И тем более, мы не сможем рассматривать последовательности интегральных сумм, соответствующих последовательностям таких разбиений с диаметрами разбиений, стремящимся к нулю. Что же понимают под такими интегралами?
. С точки зрения введенного нами понятия интеграла Римана по отрезку приведенные интегральные выражения представляются бессмыслицей. Действительно, мы не сможем составить ни одной интегральной суммы, так как никогда не кончим разбивать бесконечный промежуток на конечные отрезки и выбирать на них отмеченные точки. И тем более, мы не сможем рассматривать последовательности интегральных сумм, соответствующих последовательностям таких разбиений с диаметрами разбиений, стремящимся к нулю. Что же понимают под такими интегралами?
Приведенные интегралы называются несобственными интегралами по бесконечному промежутку и определяются они при помощи интегралов Римана по конечным отрезкам следующим образом.
Пусть функция  интегрируема на любом конечном отрезке
интегрируема на любом конечном отрезке 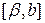 ,
,  . То есть для любого
. То есть для любого  существует
существует  . Если существует конечный предел
. Если существует конечный предел 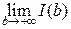 , то такой предел обозначают
, то такой предел обозначают 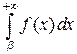 и говорят, что этот несобственный интеграл сходится. Если предел бесконечен или не существует, то говорят, что соответствующий несобственный интеграл расходится.
и говорят, что этот несобственный интеграл сходится. Если предел бесконечен или не существует, то говорят, что соответствующий несобственный интеграл расходится.
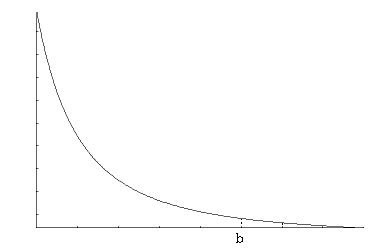
Пример. Исследуем сходимость интеграла 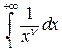 . Очевидно, что
. Очевидно, что 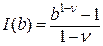 при
при 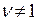 и
и 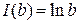 при
при 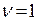 . Устремим теперь
. Устремим теперь 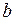 к
к 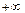 . Очевидно, что конечный предел функции
. Очевидно, что конечный предел функции 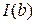 существует только при
существует только при  . Он равен
. Он равен 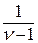 . При
. При 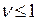 предел
предел 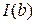 бесконечен. Таким образом, несобственный интеграл
бесконечен. Таким образом, несобственный интеграл 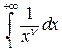 сходится только при
сходится только при  , причем
, причем 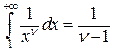 . При
. При 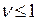 несобственный интеграл
несобственный интеграл 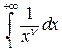
расходится.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 764; Нарушение авторских прав?; Мы поможем в написании вашей работы!