Вероятностный смысл математического ожидания

Пусть произведено «n» испытаний, в которых слу-

нятых случайной величиной, для чего разделим найден­ную сумму на общее число испытаний:

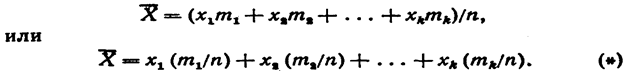
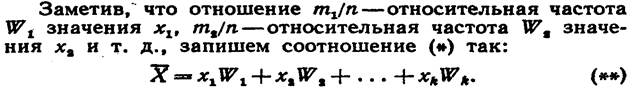
Допустим, что число испытаний достаточно велико. Тогда относительная частота приближенно равна вероят­ности появления события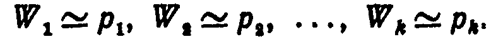

Заменив в соотношении (**) относительные частоты соответствующими вероятностями, получим

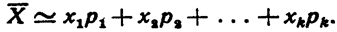
Правая часть этого приближенного равенства есть М(Х ). Итак,

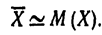
Вероятностный смысл полученного результата таков:

математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифмети­ческому наблюдаемых значений случайной величины.

Замечание 1. Легко сообразить, что математическое ожида­ние больше наименьшего и меньше наибольшего возможных значе­ний. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания.

В этом смысле математическое ожидание характеризует расположение рас­пределения и поэтому его часто называют центром распреде­ления .

Итак,математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы—их вероятностям.

Замечание 2. Происхождение термина «математическое ожи­дание» связано с начальным периодом возникновения теории вероят­ностей (XVI—XVII вв.), когда область ее применения ограничива­лась азартными играми. Игрока интересовало среднее значение ожи­даемого выигрыша, или, иными словами, математическое ожидание выигрыша.

2. Свойства математического ожидания

Свойство 1. Математическое ожидание по­стоянной величины равно самой постоянной:

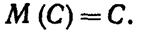
Доказательство. Будем рассматривать постоян­ную С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью р = 1. Следовательно.

Замечание 1. Определим произведение постоянной величины С на дискретную случайную величину Х как дискретную случайную СХ, возможные значения которой равны произведениям постоянной С на возможные значения X; вероятности возможных значений СХ равны вероятностям соответствующих возможных значений X. Напри­мер, если вероятность возможного значения x₁ равна p₁, то вероят­ность того, что величина СХ примет значение Сх₁, также равна р₁.

Свойство 2.

Постоянный множитель можно выно­сить за знак математического ожидания:

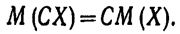
Доказательство. Пусть случайная величина Х задана законом распределения вероятностей:

Учитывая замечание 1, напишем закон распределения случайной величины СХ:

Математическое ожидание случайной величины СХ:

Итак,

Замечание 2.

Прежде чем перейти к следующему свой ству, укажем, что две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие воз­можные значения приняла другая величина. В противном случае случайные величины зависимы.

Несколько случайных величин назы­вают взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Замечание 3.

Определим произведение независимых случай­ных величин Х и У как случайную величину XY, возможные зна­чения которой равны произведениям каждого возможного значения Х на каждое возможное значение У; В ероятности возможных значе­ний произведения XY равны произведениям вероятностей возможных значений сомножителей.

Например, если вероятность возможного

Свойство 3.

Математическое ожидание произведе­ния двух независимых случайных величин равно произведе­нию их математических ожиданий:

Доказательство.Пусть независимые случайные величины Х и У заданы своими законами распределения вероятностей:

Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все воз­можные значения Х на каждое возможное значение У

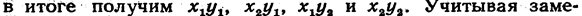
чание 3, напишем закон распределения XY, предполагая для простоты, что все возможные значения произведения различны (если это не так, то доказательство проводится аналогично):

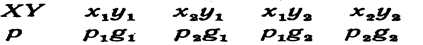
Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

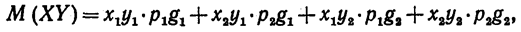
или

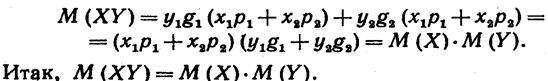
Следствие.Математическое ожидание произведе­ния нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Например, для трех случайных величин имеем:

Для произвольного числа случайных величин дока­зательство проводится методом математической индукции.

Пример 1. Независимые случайные величины Х и У заданы следующими законами распределения:

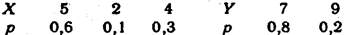
Найти математическое ожидание случайной величины XY.

Решение. Найдем математические ожидания каждой из данных величин:

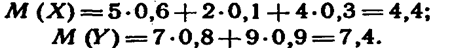
Для упрощения выкладок мы ограничились малым числом возможных значений. В общем случае доказательство аналогичное.

Случайные величины Х и У независимые, поэтому искомое ма­тематическое ожидание

Замечание 4.Определим сумму случайных величин XиY как случайную величину X + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным зна­чением У;

вероятности возможных значений X + Y для независимых величин Х и У равны произведениям вероятностей слагаемых; для зависимых величин — произведениям вероятности одного слагаемого на условную вероятность второго.

Заметим, что некоторые суммы х+у могут оказаться равными между собой. В этом случае вероятность возможного значения суммы

Следующее ниже свойство справедливо как для неза­висимых, так и для зависимых случайных величин.

Свойство 4.Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

Доказательство.Пусть случайные величины Х и Y заданы следующими законами распределения:

Составим все возможные значения величины X+Y.

Для этого к каждому возможному значению Х прибавим

возможные значения различны (если это не так, то доказательство проводится аналогично), и обозначим их ве

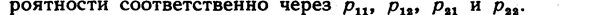
Математическое ожидание величины Х + Y равно сумме произведений возможных значений на их вероятности:

или

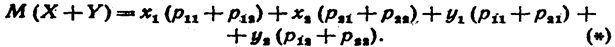Чтобы упростить вывод, мы ограничились лишь двумя возмож­ными значениями каждой из величин. В общем случае доказатель­ство аналогичное.

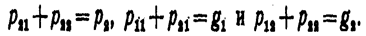
Подставляя правые части этих равенств в соотноше­ние (*), получим

или окончательно

Следствие.Математическое ожидание суммы нескольких случайных величин равно сумме математичес­ких ожиданий слагаемых.

Например,для трех слагаемых величин имеем

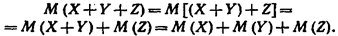
Для произвольного числа слагаемых величин доказа­тельство проводится методом математической индукции.

Пример 2. Производится 3 выстрела с вероятностями попадания в цель, равными р₁==0,4; p₂==0,3 и р₃ =0,6. Найти математическое ожидание общего числа попаданий.

Решение. Число попаданий при первом выстреле есть слу-

Общее число попаданий есть также случайная величина, состоя­щая из суммы попаданий в каждом из трех выстрелов:

Искомое математическое ожидание находим по теореме о мате- магическом ожидании суммы:

Пример 3.Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение.Обозначим число очков, которое может выпасть на первой кости, через Х и на второй—через У. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5 и 6, причем вероят­ность каждого из этих значений равна 1/6.

Найдем математическое ожидание числа очков, которые могут выпасть на первой кости:

Очевидно, что и М (У) ==7/2.

Искомое математическое ожидание

М (X + У) = М (X) + М У) = 7/2 + 7/2 = 7.

3. Теорема о математическом ожидании биномиального закона распределения

Пусть производится «п» независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна «р». Чему равно среднее число появле­ний события А в этих испытаниях? Ответ на этот вопрос дает следующая теорема.

Теорема.

Математическое ожидание М(Х) числа по­явлений события А в «n» независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

Доказательство. Будем рассматривать в качестве случайной величины Х число наступления события А в «n» независимых испытаниях. Очевидно, общее число Х появ­лений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому, если X₁ – число появлений события в первом испытании, Х₂ – во втором, …, Х_n – в «n» - м, то общее число появления события Х = X₁ + Х₂ + …. + Х_n.

По третьему свойству математического ожидания,

Каждое из слагаемых правой части равенства есть математическое ожидание числа появлений события в одном испытании: М(Х₁) – в первом, М(Х₂) – во втором и т.д.

Так как математическое ожидание числа появ­лений события в одном испытании равно вероятности события «p» (см. пример 2 учебного вопроса 1 данной лекции), то М(Х₁) = М(Х₂) = М(Х₃) =… = М(Х_n) = p.

Подставляя в правую часть равенства (*) вместо каждого слагаемого р, получим

Замечание. Так как величина Х распределена по биноми­альному закону, то доказанную теорему можно сформулировать и так: математическое ожидание биномиального распределения с па­раметрами «n» и «р» равно произведению «пр».

Пример. Вероятность попадания в цель при стрельбе из орудия р= 0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Решение.Попадание при каждом выстреле не зависит от ис­ходов других выстрелов, поэтому рассматриваемые события незави­симы и, следовательно, искомое математическое ожидание

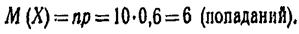
Дата добавления: 2014-01-07