Модуля 2

Конспект лекций

«Продвинутые модели и алгоритмы физического синтеза»

дисциплины
«Базовые модели и алгоритмы в САПР СБИС»

для подготовки магистров по ООП НИУ
«Физическое проектирование микро и нанометровых САПР СБИС»

профиль «Системы автоматизированного проектирования»

Лекция 5 Направленные графы. Двудольные графы. Циклические. Гиперграфы. Взвешенные графы. Граф Кёнига. Эйлеров граф. Гамильтонов граф. Планарный граф. Планаризация и проблемы планаризации графов.

Содержание:

1. Введение.

2. Основные понятия. Путь, цикл.

3. Элементарный путь и цикл.

4. Ориентированные графы.

5. Двудольные графы.

6. Гиперграфы.

7. Взвешенные графы.

8. Эйлеров путь, цикл и граф.

9. Гамильтонов путь, цикл и граф.

10. Планарные графы.

Кроме обычных графов в задачах физического синтеза зачастую используются специальные виды графов. Такие графы позволяют полнее представить модели ИС либо точнее отобразить отношения между элементами схемы. К специальным видам графов относятся направленные графы - графы, чьи ребра ориентированы от одной вершины к другой, двудольные графы или графы Кёнига, чьи вершины разбиты на два подмножества. Циклические, гамильтоновы и эйлеровы графы, которые содержат циклы и пути специального вида. Кроме того, для учета свойств не только вершин, т.е. объектов, но и отношений между этими объектами используется взвешивание ребер, что порождает взвешенные графы, так же для выделения семейств вершин часто используются гиперграфы. Далее мы рассмотрим эти группы подробнее.

Но сначала введем основные понятия.

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром. Например, рассмотрим последовательность вершин (v₁,v₂,v₃), принадлежащих графу G. Если множество ребер графа – E, содержит ребра (v₁,v₂) и (v₂,v₃), то исходная последовательность является цепью или путем в графе. Соответственно при построении путей можно ориентироваться как на выбор подмножества из множества вершин, так и подмножества из множества ребер. На первом варианте основаны например алгоритмы обхода графов в ширину и глубину, на втором – алгоритм построения остовного дерева.

Рисунок 1 Путь в графе

Циклом называют путь, в котором первая и последняя вершины совпадают. Т.е. если в последовательность из предыдущего примера добавить ее же первую вершину - (v₁,v₂,v₃,v₁) и при этом граф G содержит ребро (v₃, v₁), то такая последовательность будет являться циклом. При этом длиной пути (или цикла) называют число составляющих его рёбер (в данном случае – 3). Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Рисунок 2. Элементарный цикл

Путь (или цикл) называют простым, если ребра в нём не повторяются, т.е. подмножество ребер включает не больше одного экземпляра любого ребра из E. Такой цикл похож на скомканное веревочное кольцо – пути могут пересекаться, но никогда не идут вдоль друг друга. Число ребер, принадлежащих такому пути и выходящих из одной вершины может быть любым. Путь называется элементарным, если он простой и вершины в нём не повторяются. Такой цикл похож уже на расправленное веревочное кольцо. Из каждой вершины выходит только одно или два ребра, принадлежащих такому пути. Если это цикл, то из каждой вершины пути выходит в точности два ребра. Несложно видеть, что:

Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины. Действительно, вспомним аналогию со смятой веревкой. Если мы разрежем ее во всех местах где она касается друг друга, а потом свяжем минимальное число сегментов, то получим прямую веревку, соединяющую два своих конца.

Всякий простой неэлементарный путь содержит элементарный цикл, ведь посещая одну и ту же вершину дважды, мы должны были вернуться и описать цикл, а как мы уже знаем, всякий цикл содержит в себе элементарный цикл.

Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро). И в самом деле, если наш цикл элементарный, то задача уже решена, в противном случае всегда можно выделить элементарный подцикл.

Будем называть петлей элементарный цикл.

Рисунок 3. Орграф

Направленный или ориентированный граф (кратко орграф) это граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Дуга это такое ребро (v_i, v_j), что во все пути, содержащие v_i и v_j, эти вершины входят именно в таком порядке.

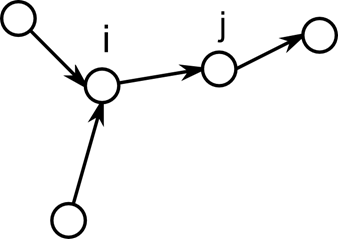
Рисунок 4. Все пути ведут от i к j

Часто такое представление удобно для случаев, когда вершины в графе не равноправны, например одна из них обладает большим потенциалом. Количество путей в таких графах, как правило, меньше, поскольку в ненаправленном графе каждому пути соответствует обратный путь, в направленном же графе порядок вершин в путях строго фиксирован. Однако для удобства, уже после представления графа в виде направленного применяется поиск путей, идущих против направления ребер. Такой прием бывает, полезен, например, при иерархическом представлении схемы. Допустим, вершинами графа являются компоненты схемы на разных уровнях иерархии. Если представить направленные ребра графа как отношение «содержит», то для ответа на вопрос, содержит ли крупный компонент маленький, требуется проделать много работы, поскольку каждый крупный компонент содержит множество маленьких, которые содержат в себе еще и еще. С другой стороны каждый маленький компонент содержится только в одном более крупном. Поэтому чтобы узнать, содержится ли он в нем достаточно один раз трассировать иерархию.

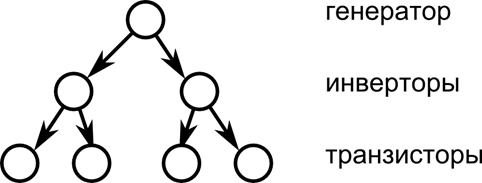
Рисунок 5. Иерархическое представление схемы

Двудольный граф или биграф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Рисунок 6. Двудольный граф

Так же двудольный граф называют графом Кёнига.

Такой граф обычно представляет схему электрических соединений. В такой схеме четко выделяются два вида компонентов – цепи и элементы схемы. Ясное дело, что цепи не могут соединяться друг с другом (иначе это была бы одна цепь), так же компоненты не могут быть «просто связаны», между ними должна пролегать хотя бы одна цепь. Таким образом, компоненты и цепи – идеальные кандидаты на группы вершин двудольного графа. В таком графе ребра будут представлять отношения «присоединен к» цепи или компоненту. Так же в алгоритме Кернигана-Лина стоимость сечения оценивается как число ребер двудольного графа, вершины которого представляют собой подмножества декомпозиции.

Гиперграф — обобщённый вид графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества вершин. Такой граф удобен для представления подмножеств на множестве вершин, например различных по напряжению участков схем или относящихся к областям, тактируемым различными сигналами. По сути, гиперграф легко приводится к двудольному графу – одно подмножество вершин – вершины гиперграфа, второе – ребра. Из-за такого однозначного соответствия гиперграфы часто не выделяют в отдельный класс.

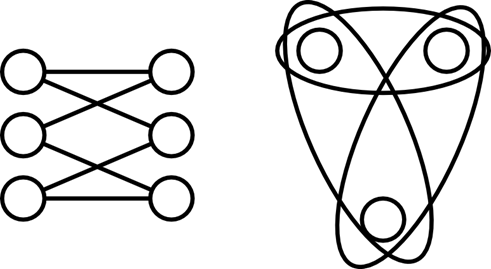
Рисунок 7. Двудольный граф и соответствующий ему гиперграф

Каждому ребру или вершине графа можно поставить в соответствие некоторое число, называемое весом. Такие графы называются взвешенными. Вес может означать площадь элемента, длину цепи или любое другое свойство моделируемого объекта. Часто вес используется при поиске путей, задача формулируется так: «найти путь с наименьшим весом», т.е. найти путь, ребра и/или вершины, входящие в который имеют меньший суммарный вес по сравнению со всеми остальными возможными путями. Часто для разных вариантов поиска ребрам и вершинам присваивают различные веса – это называется поиском по разным критериям. Иногда при поиске путей в графе в задачах, тесно связанных с топологией вес пути отождествляется с его длиной. Часто так и говорят – длина ребра. Так же в качестве свойств ребер можно использовать и другие. Например ребра графа могут быть анизотропными, вершины могут изменять направления ребер и так далее. Числовые характеристики однако хороши тем, что могут быть использованы в стандартных алгоритмах без их существенной модификации.

Рисунок 8. Пунктирный путь длиннее

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. Нахождения такого пути требует например задача о Кенигсбергских мостах: требуется пройти по каждому мосту кенигсберга, при этом не проходя нигде дважды. Если добавить к этому классическое требование вернутся в точку отправления, то получим уже задачу о поиске эйлерова цикла.

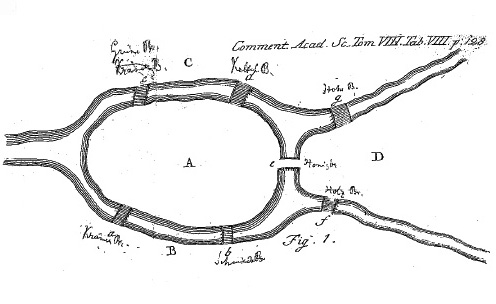
Рисунок 9. Задача о мостах

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров граф — граф, содержащий эйлеров цикл.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Отличие эйлерова и полуэйлерова графа в том, обязательно ли нам возвращатся в исходную точку. Эйлеров граф является связным и содержит вершины только четных степеней (т.е. с четным количеством примыкающих ребер). Ориентированный граф является эйлеровым, если все вершины в нем сильно связаны (т.е. для каждой пары вершин существует как прямой так и обратный путь) и в каждой вершине число входящих в нее ребер равно числу исходящих.

Более строго: Орграф называется сильно связным, если любые две его вершины сильно связаны. Две вершины s и t любого графа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s. Сильно связными компонентами орграфа называются его максимальные по включению сильно связные подграфы.

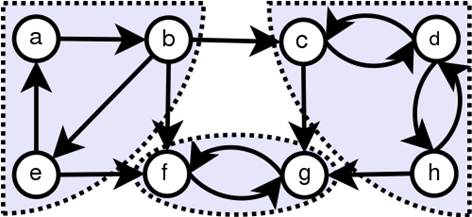
Рисунок 10. Сильно связанные компоненты графа

Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом. А гамильтонова цепь – остовным деревом.

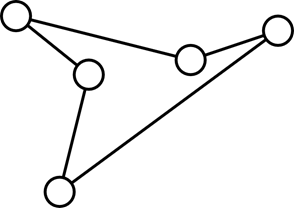
Рисунок 11. Гамильтонов (и эйлеров) цикл

Если в графе не содержится ребер, кроме входящих в гамильтонов цикл, то такой цикл является и эйлеровым.

Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру, узловые вершины которого символизировали крупнейшие города Земли, а рёбра — соединяющие их дороги.

Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Рисунок 12. Планарный и непланарный граф

Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.

Для связного плоского графа справедливо следующее соотношение между количеством вершин | V(G) |, ребер | E(G) | и граней | F(G) | (включая внешнюю грань):

| V(G) | − | E(G) | + | F(G) | = 2

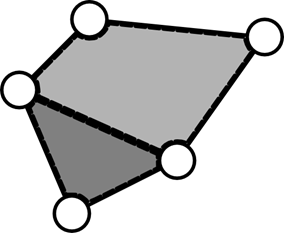
Рисунок 13. Грани планарного графа

Оно было найдено Эйлером в 1736 г. при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум.

Критерий непланарности:

· достаточное условие — если граф содержит двудольный подграф K_3,3 или полный подграф K₅, то он является не планарным;

· необходимое условие — если граф не планарный, то он должен содержать больше 4 вершин, степень которых больше 3, или больше 5 вершин степени больше 2.

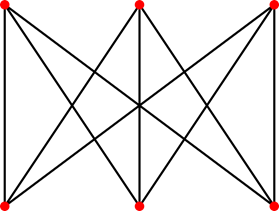
Рисунок 14. К_3,3

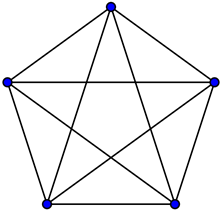
Рисунок 15. К₅

Планарными графами являются большинство графов, используемых на этапе физического синтеза – трассировочная сетка, графы вертикальных и горизонтальных ограничений.

Практический пример:

DCCC(direct-current connected component) или компонентом объединенным по постоянному току называется часть электрической схемы, такая, что при любых сигналах на входах этой части схемы токи протекают только внутри нее. Например, инвертор или элемент ИЛИ-НЕ в схемотехнике КМОП являются DCCC, поскольку ток не протекает через затворы полевых транзисторов.

Для нахождения таких компонентов в произвольной части схемы можно использовать направленные графы, рассмотрим например элемент 2И:

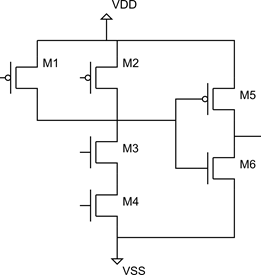
Рисунок 16 Схема элемента 2И

Не сразу понятно, какие части схемы являются DCCC. Конечно, используя метод «пристального взгляда», нарисовав все возможные токи, и перебрав все входные состояния, мы рано или поздно выделим независимые компоненты. Однако что делать, если транзисторов будет несколько десятков или сотен? Попробуем формализовать задачу. Для этого представим узлы схемы в виде вершин направленного графа, а элементы в виде ребер. Поскольку ток не может течь через затвор МОП-транзистора, то такой транзистор будет представлен в виде одного ребра, соединяющего исток и сток. Пусть так же направление ребер показывает направление тока текущего через транзистор.

Через p-канальные транзисторы ток течет от шины питания(VDD) к выходу схемы, а через n-канальные от выхода на шину земли (VSS). Построим орграф, соответствующий нашей схеме.

Теперь найдем все пути, которые ведут из вершины VDD в вершину VSS. Таких путей три – (M1, M3, M4), (M2, M3, M4), (M5, M6). Ясно, что ток выбравший первый или второй путь обязательно пройдет через транзисторы М3 и М4, поэтому все транзисторы первых двух путей относятся к одному DCCC. Третий путь не содержит общих транзисторов ни с одним другим путем, поэтому представляет собой еще один DCCC.

Рисунок 17 Графовая модель схемы 2И

Итак, для того чтобы найти все компоненты DCCC в КМОП схеме необходимо:

1. Построить орграф схемы, где каждому узлу соответствует вершина, а каждому транзистору – ребро, ориентированное в направлении течения тока через этот транзистор.

2. Найти все пути, соединяющие шины земли и питания.

3. Если два пути имеют хотя бы один общий элемент, то все элементы этих путей принадлежат к одному DCCC.

В качестве упражнения найдите все DCCC для схемы, представленной на рисунке.

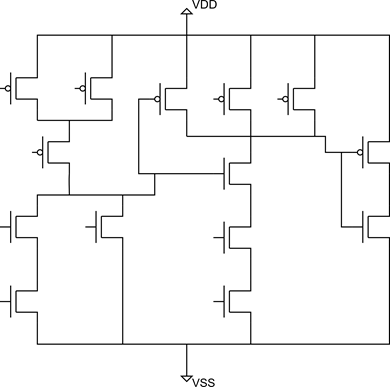
Рисунок 18 Задание для самостоятельного поиска DCCC

Вопросы и задания для самостоятельной проработки:

1. Придумайте или найдите в литературе алгоритм для определения наличия циклов в графе ([4]).

2. Разработайте набор формализованных критериев для определения элементарного пути и цикла в графе ([2] стр. 69-83).

3. Всегда ли можно так ориентировать ребра в ненаправленном графе с циклом, чтобы результирующий орграф тоже содержал цикл? Приведите примеры ([2] стр. 157-227).

4. Приведите примеры взаимного соответствия гиперграфов и двудольных графов. Можно ли однозначно сопоставлять гиперграфы и другие типы графов? Приведите примеры ([6] гл. IX).

5. Приведите примеры планарного и непланарного графа. Приведите пример планарного и непланарного графа, которые отличаются одним ребром ([1] ч. 5).

Список литературы:

1. А. Ю. Ольшанский. Плоские графы

2. Седжвик Р. Фундаментальные алгоритмы на С++. Часть 5

3. http://www.univer.omsk.su/departs/compsci/kursi/disc/graphs.htm

4. http://e-maxx.ru/algo/

5. http://rain.ifmo.ru/cat/view.php/theory/list

6. http://vmg.pp.ua/books/Математика/Графы/Емеличев%20В.А.%20и%20др.%20Лекции%20по%20теории%20графов/

Лекция 6 Понятие о дереве. Канонический код дерева. Обход дерева. Специальные виды деревьев. Бинарные деревья. Черно-красные деревья. Рассеченные множества. Балансированные деревья. k-мерные деревья. Дерево как модель данных.

Содержание:

1. Понятие о дереве.

2. Остовное дерево.

3. Минимальное остовное дерево.

4. Канонический код графа.

5. Поиск в глубину и ширину.

6. Двоичное дерево.

7. Двоичная куча.

8. Красно-черное дерево.

9. Система непересекающихся множеств.

10. Б-дерево.

Дерево — это связный ациклический граф (то есть граф, не содержащий циклов, между любой парой вершин которого существует ровно один путь). Деревья связывают все вершины графа.

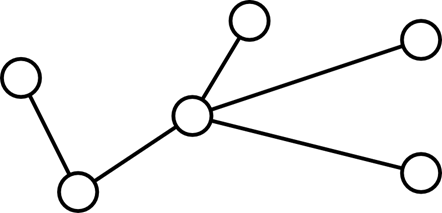
Рисунок 19. Дерево

Остовным деревом графа называется дерево, построенное на множестве вершин графа с использованием подмножества его ребер. Для построения дерева можно воспользоваться двумя подходами. Конструктивный подход состоит в том, чтобы сначала произвольно выбрать ребро, соединяющее две вершины графа. Назовем получившуюся структуру деревом. Найдем ребро, которое соединяет вершину дерева с вершиной вне дерева, и добавим его в дерево. Как только мы не сможем найти ни одного такого ребра – построение дерева завершено. В деструктивном подходе мы находим цикл в графе и удаляем из него произвольное ребро. Поскольку концы этого ребра входят в цикл, то граф не потеряет связности. Повторяя эту операцию пока в графе не останется ни одного цикла мы получим остовное дерево.

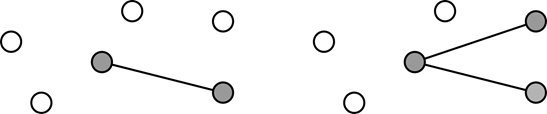
Рисунок 20. Конструктивное построение дерева

Часто в задачах физического синтеза требуется найти минимальное остовное дерево. Такая задача ставится для взвешенных графов. Под минимальностью здесь подразумевается минимальность суммы весов ребер входящих в дерево. Такая задача может быть полезна, например для нахождения конфигурации цепи, соединяющей несколько выводов разных элементов. Так как при ее решении образуется оставное дерево, то все выводы будут соединены, а так как мы ищем минимальное дерево, то длина цепей тоже будет минимальна.

Наиболее известным алгоритмом для решения этой задачи является алгоритм Краскала:

- найти ребро с минимальным весом и добавить его к дереву;

- пока построение дерева не завершено:

- найти ребро минимального веса, не входящее в дерево и не образующее циклов в дереве

- добавить его в дерево

Так же используется алгоритм Прима: построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву присоединяется самое лёгкое из рёбер, соединяющих вершину из построенного дерева, и вершину не из дерева.

Число ребер E в дереве с числом вершин n:

E = n - 1

Канонический код графа (graph canonical code) — это уникальная строка, которая не зависит от порядка нумерации вершин. У изоморфных графов одинаковые канонические коды, у неизоморфных — разные.

Вершины и рёбра графа могут быть снабжены дополнительными метками (цветами). В этом случае канонический код включает в себя цветовые идентификаторы.

Канонические коды графов позволяют избавиться от дорогостоящей процедуры проверки изоморфизма (graph isomorphism), и определять совпадение графов по сравнению строк.

Например, как найти дубликаты в множестве N графов? Вычислить N канонических кодов, отсортировать их и последовательно сравнить. Гораздо выгоднее, чем делать N*(N-1)/2 проверок изоморфизма. Можно сказать, что канонический код — это хеш-код без промахов.

Канонический код может выглядеть по-разному: как матрица смежности, развёрнутая в строку, или как маршрут обхода графа в ширину, или в глубину. Какое представление выбрать, не столь важно. Задача в любом случае сводится к вычислению канонической нумерации вершин (canonical numbering, canonical labeling). Каноническая нумерация — это нумерация (перестановка) вершин графа, гарантирующая, что изоморфные графы будут пронумерованы одинаково. Получив нужную перестановку, уже не составит труда построить канонический код, например, по обходу графа в глубину: начать обход с вершины под номером 1 и при ветвлении выбирать ту вершину, «канонический номер» которой меньше.

Рисунок 21. Поиск в ширину. Цифрами обозначен порядок обхода. Более светлые обходятся после темных.

Поиск в ширину (BFS, Breadth-first search) — метод обхода и разметки вершин графа.

Поиск в ширину выполняется в следующем порядке: началу обхода s приписывается метка 0, смежным с ней вершинам — метка 1. Затем поочередно рассматривается окружение всех вершин с метками 1, и каждой из входящих в эти окружения вершин приписываем метку 2 и т. д.

Если исходный граф связный, то поиск в ширину пометит все его вершины. Дуги вида (i, i+1) порождают остовный бесконтурный орграф, содержащий в качестве своей части остовное ордерево, называемое поисковым деревом.

Легко увидеть, что с помощью поиска в ширину можно также занумеровать вершины, нумеруя вначале вершины с меткой 1, затем с меткой 2 и т. д.

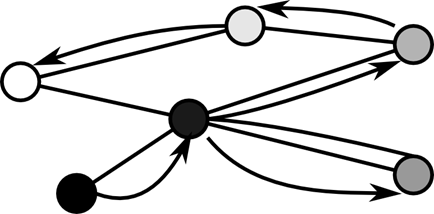
Рисунок 22. Поиск в глубину.

Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.

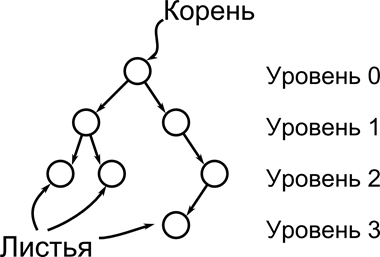
Рисунок 23. Двоичное дерево

Двоичное дерево — древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Каждый узел содержит какую-то информацию – свойства, величины, ссылки и так далее. Можно сказать, что двоичное дерево это ориентированное дерево. У каждой вершины в нем, кроме одной, называемой корневой или просто корнем есть родитель. Вершины, у которых нет наследников, называются листьями.

Как правило такие деревья разбивают на уровни. На 0 уровне содержится только корень дерева, на 1 – до двух его наследников(потомков), на 2 – до четырех их наследников и так далее. Говорят что дерево сбалансировано, если число его уровней (то есть уровней, на которых есть хотя бы один элемент (вершина дерева)) равно log₂(n), где n – общее число вершин дерева.

Для практических целей обычно используют два подвида бинарных деревьев — двоичное дерево поиска и двоичная куча.

Рисунок 24. Двоичное дерево поиска

Двоичное дерево поиска содержит в каждой вершине значение некоторого типа, для которого определена операция «меньше». Двоичное дерево называется деревом поиска, если для каждой его вершины значение ее левого потомка «меньше» собственного значения, а правого «не-меньше» собственного. В сбалансированном двоичном дереве корень лежит примерно в середине диапазона возможных значений. При этом в левом поддереве лежат значения меньше, а в правом не меньше корня. Поэтому при поиске в подобном дереве требуется всего log₂(n) операций (по одной на каждый уровень дерева) чтобы найти искомое значение. Чем хуже сбалансировано дерево, тем больше эта оценка будет отличатся от логарифма.

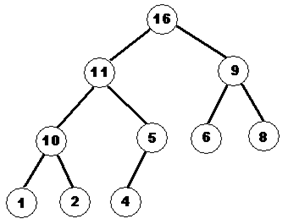
Рисунок 25. Двоичная куча

Двоичная куча это такое двоичное дерево, в котором каждая вершина не меньше своих потомков (или не больше). Кроме того для того чтобы дерево было кучей, требуется чтобы оно было идеально сбалансировано, т.е. все его вершины должны иметь и правого и левого потомка, за исключением всех вершин последнего уровня и возможно части вершин предпоследнего. Все поддеревья всех вершин этого дерева так же являются кучами. Кучи удобно использовать для сортировки массива «на месте». Для этого нужно построить кучу из массива, а потом перенести ее корень в конец массива. Построив кучу на оставшихся элементах мы снова сможем повторить процедуру. Такая сортировка называется пирамидальной или сортировкой кучей (heapsort).

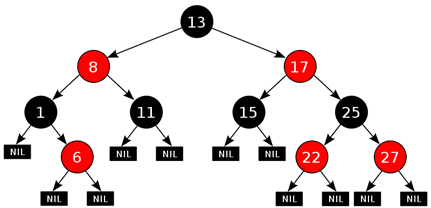
Рисунок 26. Красно-черное дерево

Красно-чёрное дерево (англ. Red-Black-Tree, RB-Tree) — это одно из самобалансирующихся двоичных деревьев поиска, гарантирующих логарифмический рост высоты дерева от числа узлов и быстро выполняющее основные операции дерева поиска: добавление, удаление и поиск узла. Сбалансированность достигается за счёт введения дополнительного атрибута узла дерева — «цвета». Этот атрибут может принимать одно из двух возможных значений — «чёрный» или «красный». Красно-чёрное дерево — двоичное дерево поиска, в котором каждый узел имеет атрибут цвет, принимающий значения красный или черный. В дополнение к обычным требованиям, налагаемым на двоичные деревья поиска, к красно-чёрным деревьям применяются следующие требования:

1. Узел либо красный, либо чёрный.

2. Корень — чёрный. (В других определениях это правило иногда опускается. Это правило слабо влияет на анализ, так как корень всегда может быть изменен с красного на чёрный, но не обязательно наоборот).

3. Все листья — черные.

4. Оба потомка каждого красного узла — черные.

5. Всякий простой путь от данного узла до любого листового узла, являющегося его потомком, содержит одинаковое число черных узлов.

Эти ограничения реализуют критическое свойство красно-черных деревьев: путь от корня до самого дальнего листа не более чем в два раза длиннее пути от корня до ближайшего листа. Результатом является то, что дерево примерно сбалансировано. Так как такие операции как вставка, удаление и поиск значений требуют в худшем случае времени, пропорционального длине дерева, эта теоретическая верхняя граница высоты позволяет красно-чёрным деревьям быть более эффективными в худшем случае, чем обычные двоичные деревья поиска.

Чтобы понять, почему это гарантируется, достаточно рассмотреть эффект свойства 4 и 5 вместе. Пусть для красно-чёрного дерева T число черных узлов в свойстве 5 равно B. Тогда кратчайший возможный путь от корня дерева T до любого листового узла содержит B черных узлов. Более длинный возможный путь может быть построен путем включения красных узлов. Однако, свойство 4 не позволяет вставить несколько красных узлов подряд. Поэтому самый длинный возможный путь состоит из 2B узлов, попеременно красных и черных. Любой максимальный путь имеет одинаковое число черных узлов (по свойству 5), следовательно, не существует пути, более чем вдвое длинного, чем любой другой путь.

Во многих реализациях структуры дерева возможно, чтобы узел имел только одного потомка и листовой узел содержал данные. В этих предположениях реализовать красно-чёрное дерево возможно, но изменятся несколько свойств и алгоритм усложнится. По этой причине данная статья использует «фиктивные листовые узлы», которые не содержат данных и просто служат для указания, где дерево заканчивается. Эти узлы часто опускаются при графическом изображении, в результате дерево выглядит противоречиво с вышеизложенными принципами, но на самом деле противоречия нет. Следствием этого является то, что все внутренние (не являющиеся листовыми) узлы имеют два потомка, хотя один из них может быть нулевым листом. Свойство 5 гарантирует, что красный узел обязан иметь в качестве потомков либо два черных нулевых листа, либо два черных внутренних узла. Для чёрного узла с одним потомком нулевым листовым узлом и другим потомком, не являющимся таковым, свойства 3, 4 и 5 гарантируют, что последний должен быть красным узлом с двумя черными нулевыми листьями в качестве потомков.

Иногда красно-чёрное дерево трактуют как бинарное дерево поиска, у которого вместо узлов в красный и чёрный цвета раскрашены ребра, но это не имеет какого-либо значения.

Популярность красно-чёрных деревьев связана с тем, что на них часто достигается подходящий баланс между степенью сбалансированности и сложностью поддержки сбалансированности. В частности, при сравнении с идеально сбалансированными деревьями часто обнаруживается, что последние имеют слишком жесткое условие сбалансированности и при выполнении операций удаления из дерева много времени тратится на поддержание необходимой сбалансированности.

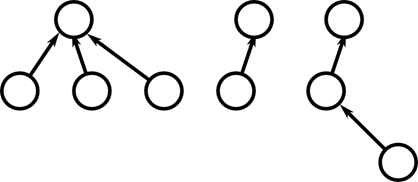
Рисунок 27. Система непересекающихся множеств

Система непересекающихся множеств позволяет администрировать множество элементов, разбитое на непересекающиеся подмножества. При этом каждому подмножеству назначается его представитель — элемент этого подмножества. Абстрактная структура данных определяется множеством трех операций {Union, Find, MakeSet}.

Система непересекающихся множеств очень удобна для хранения компонент связности в графах. К примеру, Алгоритму Краскала необходима подобная структура данных для эффективной реализации.

В этой структуре каждое множество представлено в виде дерева с одним корневым элементом. Каждая вершина в этом множестве имеет ссылку только на своего родителя. Верно что для каждой вершины поднимаясь по иерархии родителей мы придем к корню множества и только к нему. Таким образом осуществляется операция Find. Операция Union осуществляется назначением корня одного из множеств родителем корня другого множества. MakeSet позволяет создать новое пустое множество, содержащее только корневой элемент.

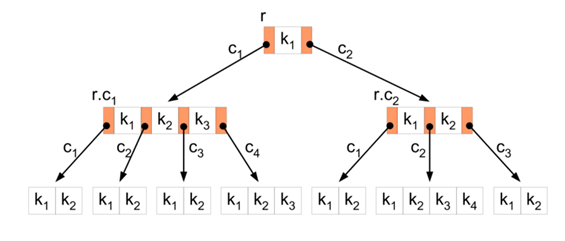
Рисунок 28. Б-дерево

Б-дерево — структура данных, дерево поиска. С точки зрения внешнего логического представления, сбалансированное, сильно ветвистое дерево во внешней памяти.

Использование B-деревьев впервые было предложено Р. Бэйером (англ. R. Bayer) и Е. МакКрейтом в 1970 году.

Сбалансированность означает, что длина любых двух путей от корня до листов различается не более, чем на единицу.

Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков.

С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, то есть каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.

Структура B-дерева применяется для организации индексов во многих современных СУБД.

B-дерево может применяться для структурирования (индексирования) информации на жёстком диске (как правило, метаданных). Время доступа к произвольному блоку на жёстком диске очень велико (порядка миллисекунд), поскольку оно определяется скоростью вращения диска и перемещения головок. Поэтому важно уменьшить количество узлов, просматриваемых при каждой операции. Использование поиска по списку каждый раз для нахождения случайного блока могло бы привести к чрезмерному количеству обращений к диску, вследствие необходимости осуществления последовательного прохода по всем его элементам, предшествующим заданному; тогда как поиск в B-дереве, благодаря свойствам сбалансированности и высокой ветвистости, значительно позволяет сократить количество таких операций.

Относительно простая реализация алгоритмов и существование готовых библиотек (в том числе для C) для работы со структурой B-дерева обеспечивают популярность применения такой организации памяти в самых разнообразных программах, работающих с большими объёмами данных.

Практический пример:

Межсоединения в СБИС состоят из множества прямоугольных сегментов. Для того чтобы проверить соответствие топологии схеме необходимо узнать к каким цепям принадлежат эти сегменты. Для решения части этой задачи попробуем найти все сегменты, которые пересекаются друг с другом. Такие сегменты гарантированно входят в одну цепь, так как они электрически соединены. Рассмотрим простой пример. Пусть у нас есть три сегмента – 1, 2 и 3. Отнесем их к трем различным цепям – красной, зеленой и синей.

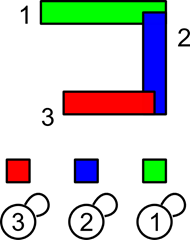
Рисунок 29 Начальное состояние

Список сегментов, принадлежащих одной цепи, представим в виде дерева с единственным исключением – циклом у корня. Вершина, которая является собственным родителем – это корень. То, что вершина является корнем, можно было обозначить с помощью любого другого признака – флага вершины, нулевого родителя и т.п. Это не принципиально.

Произвольным способом найдем теперь, что сегменты 1 и 2 пересекаются, значит, они оба принадлежат к одной цепи. Пусть эта объединенная цепь в дальнейшем называется зеленой.

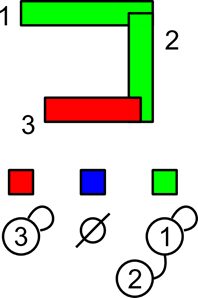
Рисунок 30 Первый шаг

Чтобы указать, что второй сегмент переходит во множество, которому принадлежит первый сегмент, сделаем первый сегмент родителем второго. Аналогично поступаем со 2 и 3 сегментом.

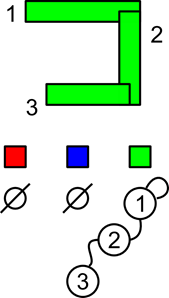
Рисунок 31 Конечное состояние

В результате мы увидим, что все сегменты принадлежат зеленому множеству, а значит и входят в одну цепь. Повторяя данный алгоритм для всех случаев пересечения сегментов в схеме, мы получим множество всех цепей схемы.

Вопросы и задания для самостоятельной проработки:

1. Сколько деревьев существует как подмножество конкретного графа? Приведите примеры ([3]).

2. Может ли граф содержать несколько минимальных остовных деревьев? Приведите примеры([3]).

3. Предложите несколько видов канонического кода для произвольного графа([5]).

4. Подберите примеры для иллюстрации превосходства поиска в ширину над поиском в глубину и наоборот ([1] стр. 99, 132).

5. Покажите соответствие между двоичной кучей и двоичным деревом ([2] стр. 178 – 193).

6. Разработайте операцию вставки в красно-черное дерево ([2] стр. 336-364).

7. Предложите эвристики для улучшения скорости поиска в системе непересекающихся множеств ([2] стр. 1296).

Список литературы:

1. Седжвик Р. Фундаментальные алгоритмы на С++. Часть 5

2. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Introduction to algorithms. — 2-е изд.

3. http://www.lvf2004.com/dop_t4r13part1.html

4. http://ric.uni-altai.ru/Fundamental/pascal3/lab7/teor7-4.htm

5. http://www.lib.tsu.ru/mminfo/000349342/01/image/1-101.pdf

Лекция 9 Иерархическое разбиение пространства. Плоская укладка. BSP-деревья. kd-деревья. Квадродерево.

Содержание:

1. Введение.

2. Разбиение на сектора.

3. Плоская укладка.

4. Двоичное разбиение пространства.

5. kd-дерево.

6. Квадродерево.

7. R-дерево.

Во многих задачах физического синтеза требуется работа с пространственными отношениями объектов. Требуется искать пересечения прямоугольников, считать их расстояние друг до друга. Часто объектов, с которыми требуется работать – многие тысячи. Для того чтобы не перебирать их все в поисках подходящего применяются методы иерархического (и не только) разбиения пространства. Основная идея всех этих методов в том, что объекты группируются соответственно своему расположению в пространстве, что отсекает ненужные проверки – например проверку пересечения объектов, находящихся в другой части кристалла.

Одним из самых простых способов разбиения является разбиение на сектора. Все пространство, в котором могут находиться элементы, разбивается на сектора, обычно прямоугольные. После этого, для каждого элемента вычисляется сектор, в котором он находится и это значение (номер сектора) записывается в метаданные элемента. Теперь, чтобы узнать, пересекаются два объекта или нет, достаточно сравнить номера секторов этих объектов. Если номера разные, то объекты точно не пересекаются. Если же они одинаковые, можно запустить более точную процедуру проверки. Таким образом, большая часть объектов будет отсеяна на первой стадии проверки, что позволяет сильно ускорить вычисления.

Рисунок 32. Разбиение на сектора

Тонким моментом является присутствие элемента на границе секторов. Какому сектору принадлежит такой элемент? Какой бы сектор мы не выбрали, всегда есть вероятность, что мы пропустим пересечение с объектом, который находится близко к границе, но не в том секторе, который мы выбрали для данного элемента. Тут приходится идти на компромисс и запускать точную проверку для всех смежных секторов, либо считать, что элемент лежит сразу во всех секторах, в которых лежит хотя бы его часть.

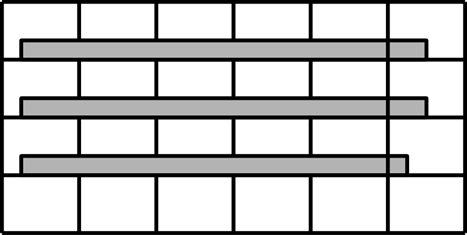
Рисунок 33. В каком секторе расположены объекты?

Проблема частично решается так же увеличением размеров секторов относительно элементов. При этом элементы все реже будут оказываться сразу в нескольких секторах. Однако такой подход влечет за собой более частые проверки пересечения, поскольку в один сектор будет подать больше элементов.

Важным топологическим алгоритмом является плоская укладка - это расположение элементов на плоскости с помощью последовательного деления этой плоскости секущими. Существуют различные виды плоской укладки, зависящие от числа секущих на каждом шаге. Мы будем рассматривать ПУ-2 с одной секущей и соответственно двумя областями.

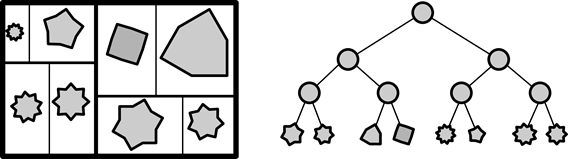
Рисунок 34. ПУ-2 и дерево декомпозиции

Для того чтобы применить алгоритм к какому либо множеству элементов, для начала нужно произвести его иерархическую бинарную декомпозицию. Для этого первым делом каждому элементу назначается «вес», прямо связанный с площадью, занимаемой этим элементом. Затем строится дерево декомпозиции. Дерево декомпозиции – это бинарное дерево, листьями которого являются все элементы множества, а корнем все множество в целом. На первом шаге отмечается корень дерева, включающий все множество. Затем это множество разбивается на две примерно равные (по сумме весов элементов) части. Каждый элемент может входить только в одно это подмножество. Эти подмножества отмечаются как левый и правый потомок корня дерева. Затем процедура повторяется для каждого из этих потомков. Рекурсивно повторяя данные шаги до тех пор, пока в каждом потомке не останется по одному элементу, мы и получим дерево декомпозиции.

Корень этого дерева соответствует всей области размещения элементов. Разделим эту область пополам, так чтобы отношение площадей половин было таким же, как и отношение весов потомков корня. Как вы уже догадались: проделаем ту же процедуру рекурсивно для всех потомков корня. В результате мы получим разбиение плоскости, в котором для каждого элемента определена область, куда он будет помещен. Так как разбиение плоскости на две можно провести двумя способами, выбирается тот, при котором дочерние области имеют соотношение сторон, ближайшее к соотношению сторон родителя.

Такое разбиение позволяет эффективно использовать площадь – задача, которую часто пытаются решить при расположении элементов СБИС. Однако качество решения очень сильно зависит от качества декомпозиции, кроме того не гарантируется глобальная оптимальность решения, поскольку алгоритм «жадный» - на каждом шаге принимает локально-оптимальное решение. Например если элемент, чья оптимальная позиция в левой части плоскости попадает при декомпозиции в правое поддерево, то уже нет способа вернуть его обратно.

Плотная укладка, как вы уже, наверное, заметили, является иерархическим разбиением пространства, в отличие от разбиения его на сектора. Иерархическое разбиение характеризуется более сложной, вложенной структурой данных, представляющих пространственные группы. Обычно для такой структуры выбирают дерево, так как оно является естественным представлением иерархии (вспомните например генеалогическое дерево).

BSP-дерево — это структура данных, используемая в трехмерной графике. Аббревиатура BSP означает Binary Space Partition — двоичное разбиение пространства. BSP-дерево используется для эффективного выполнения следующих операций:

· Сортировки визуальных объектов в порядке удаления от наблюдателя;

· Обнаружение столкновений.

BSP-деревья были впервые применены специалистами компании Lucas Arts в начале 80-х годов. Популярность у разработчиков они завоевали благодаря компании id Software, разработавшей движки Doom (1993) и Quake (1996).

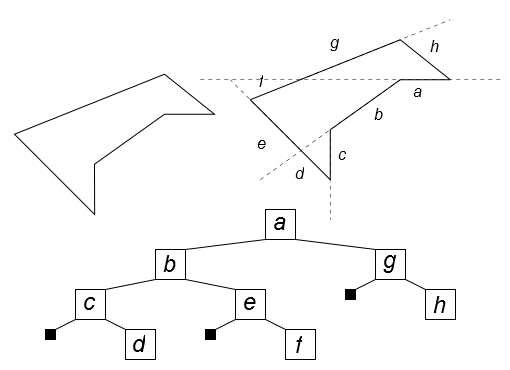
Рисунок 35. BSP-дерево

В BSP-дереве каждый узел связан с разбивающей прямой или плоскостью в 2-мерном или 3-мерном пространстве соответственно. При этом все объекты, лежащие с фронтальной стороны плоскости относятся к фронтальному поддереву, а все объекты, лежащие с оборотной стороны плоскости относятся к оборотному поддереву. Для определения принадлежности объекта к фронтальной или оборотной стороне разбивающей прямой или плоскости необходимо исследовать положение каждой его точки. Положение точки относительно плоскости определяется скалярным произведением нормали плоскости и координат точки в однородных координатах. Возможно три случая:

1. Скалярное произведение больше 0 — точка лежит с фронтальной стороны плоскости;

2. Скалярное произведение равно 0 — точка лежит на плоскости;

3. Скалярное произведение меньше 0 — точка лежит с обратной стороны плоскости.

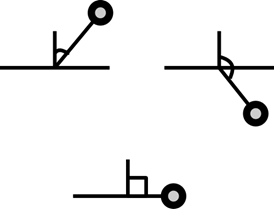
Рисунок 36. Скалярное произведение

Если для всех точек объекта скалярное произведение больше или равно 0, то он относится к фронтальному поддереву. Если для всех точек объекта скалярное произведение меньше или равно 0, то он относится к оборотному поддереву. Если для всех точек объекта скалярное произведение равно 0, то не играет роли к какому поддереву он принадлежит. Если скалярные произведения для точек объекта имеют разный знак, то он рассекается разбивающей плоскостью так, чтобы полученные объекты лежали только с фронтальной или только с оборотной стороны. Для каждого подузла BSP-дерева справедливо вышеприведенное утверждение, с тем исключением, что рассмотрению подлежат только те объекты, которые принадлежат к фронтальной или оборотной стороне разбивающей плоскости родительского узла.

Важным для BSP дерева является выбор рассекающих плоскостей. От этого зависит, насколько сбалансированным будет дерево, то есть насколько быстрым будет поиск элементов в нем. Как вы уже догадались, дерево декомпозиции для плоской укладки является BSP деревом. Только для него решается обратная задача – размещение объектов на плоскости так, чтобы они попали в уже сформированную структуру BSP дерева.

Рассмотрим структуру бинарного пространственного разбиения, называемая kd-дерево. Эта структура представляет собой бинарное дерево ограничивающих параллелепипедов, вложенных друг в друга. Каждый параллелепипед в kd-дереве разбивается плоскостью, перпендикулярной одной из осей координат на два дочерних параллелепипеда.

Рисунок 37. kd-дерево разбивает плоскость на области

Вся сцена целиком содержится внутри корневого параллелепипеда, но, продолжая рекурсивное разбиение параллелепипедов, можно прийти к тому, что в каждом листовом параллелепипеде будет содержаться лишь небольшое число примитивов. Таким образом, kd-дерево позволяет использовать бинарный поиск для нахождения примитива, пересекаемого лучом.

Отличием трехмерного случая является то, что кроме положения секущей плоскости есть три способа ее провести – перпендикулярно каждой из осей координат.

Плоская укладка и kd-дерево являются лишь частными случаями бинарного разбиения пространства, когда разбивающая плоскость ортогональна осям координат. Такое ограничение не случайно, оно позволяет легче считать пересечение объектов с линиями и плоскостями сечения. Действительно, для того чтобы определить, лежит точка спереди или сзади плоскости, перпендикулярной какой либо из осей, достаточно сравнить эту координату плоскости и точки. Кроме того вы видите, что для хранения информации о сечении достаточно одной координаты и указания – вертикальное это, горизонтальное или для трехмерного случая еще один вид сечения.

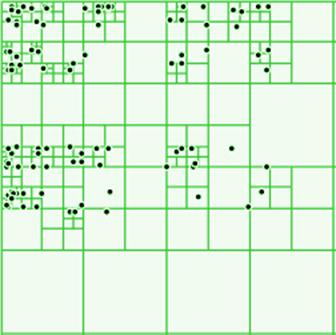
Рисунок 38. Разбиение плоскости квадродеревом

Стоит заметить, что для случая, когда множество элементов не меняет своего положения достаточно один раз вычислить дерево. В таком случае более выгодным может оказаться рассечение плоскости наклонными линиями, а пространства – наклонными плоскостями. Способ разбиения следует выбирать исходя из динамики разбиваемого множества, количества и размера элементов, а так же имеющихся вычислительных мощностей.

Однако что будет, если разбить пространство не на две части, а например на четыре? Такое решение сильно уменьшает высоту дерева, однако усложняет поиск. Можно назвать такое решение комбинацией иерархического разбиения и разбиения на секторы. Для двумерного случая существует квадродерево, в котором каждый узел имеет четырех потомков, а для трехмерного октодерево.

Рисунок 39. Квадродерево

В квадро- и октодереве потомки имеют одинаковый размер, это позволяет не хранить координаты секущих плоскостей (они всегда лежат посередине области текущего узла. Кроме того в таких структурах используется соглашение о перпендикулярности секущих линий и плоскостей координатным осям. Такой подход позволяет при уменьшении потребления памяти, что может быть критично для количества элементов, характерных для современных СБИС, добиваться серьезного ускорения пространственных операций.

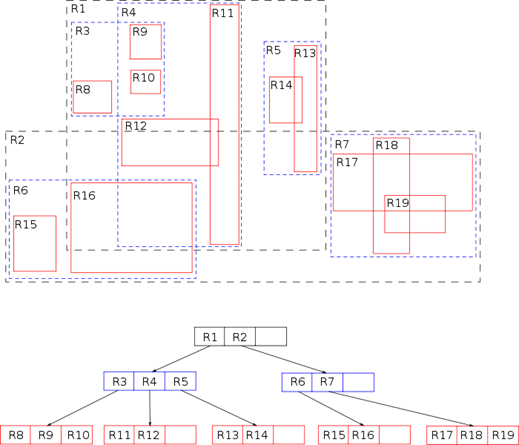
Рисунок 40. R-дерево

Тут можно спросить: зачем мы группируем пустое место? Давайте группировать объекты! Для решения подобной задачи подходит R-дерево или дерево прямоугольников. Такое дерево больше всего похоже на B-дерево для числовых значений. Только каждая вершина представляет собой набор прямоугольников, каждый из которых ссылается на дочернюю вершину и включает все её прямоугольники. Такое представление позволяет снизить чувствительность дерева к добавлению и удалению элементов, однако делает важным порядок вставки. При добавлении элемента ищется вершина, в которую можно добавить его, минимально расширяя охватывающий прямоугольник этой вершины. Если в этой вершине и так достаточно элементов (максимальное количество элементов в вершине является параметром дерева), то вершина расщепляется на несколько вершин.

Иногда вместо R-дерева используют так называемое cR-дерево (c означает clustered). Основная идея в том, что для разделения вершин или точек используются алгоритмы кластеризации, такие как k-means. Сложность k-means тоже линейная, но он в большинстве случаев даёт лучший результат, чем линейный алгоритм разделения Гуттмана, в отличие от которого он не только минимизирует суммарную площадь огибающих параллелепипедов, но и расстояние между ними, и площадь перекрытия. Для кластеризации точек используется выбранная метрика исходного пространства, для кластеризации вершин можно использовать расстояние между центрами их огибающих параллелепипедов или максимальное расстояние между ними.

Алгоритмы кластеризации не учитывают то, что число потомков вершины ограничено сверху и снизу константами алгоритма. Если кластерный сплит выдаёт неприемлемый результат, можно использовать для этого набора классический алгоритм, так как на практике такое происходит не часто.

Интересна идея использовать кластеризацию на несколько кластеров, где несколько может быть больше двух. Однако надо учитывать, что это накладывает определённые ограничения на параметры структуры р-дерева.

Отметим, что помимо cR-дерева существует его вариация clR-дерево, основанное на методе кластеризации, где в качестве центра использован итерационный алгоритм решения «задачи размещения». Алгоритм имеет квадратичную вычислительную сложность, но обеспечивает построение более компактных огибающих параллелепипедов в записях вершин структуры.

Поиск в дереве довольно тривиален, надо лишь учитывать тот факт, что каждая точка пространства может быть покрыта несколькими вершинами.

Практический пример:

Предположим, что у нас имеется область кристалла, в которой две точки требуется соединить проводником. Для того чтобы определить какие препятствия возникнут на пути можно поискать пересечения с каждым элементом схемы. Однако если таких элементов большое количество, то это может занять длительное время. Посмотрим, как квадродерево поможет решить проблему поиска пересечений. Ниже представлен фрагмент нашего кристалла. Зеленым обозначены препятствия, красным – необходимый путь проводника. Область уже поделена на квадраты для построения вершин квадродерева. Разбиение остановлено, когда квадродерево достигло второго уровня, чтобы упростить пример.

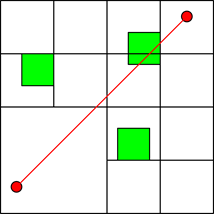
Рисунок 41 Разбиение площади кристалла

Посмотрим на результирующее дерево. Зеленым отмечены вершины с препятствиями, белым – пустые области. Узлы расположенные слева направо, на плоскости расположены против часовой стрелки, начиная с левого нижнего угла.

Рисунок 42 Квадродерево

Для начала найдем какому узлу находится стартовая точка. Начнем с корневого узла, который представляет всю плоскость. Используя координаты точки найдем что она находится в нижнем левом квадрате. Это первый узел, он пуст (красная стрелка).

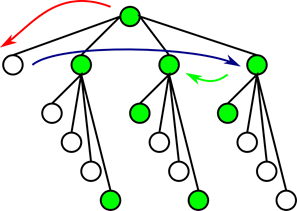
Рисунок 43 Порядок обхода квадродерева

Теперь посмотрим, с какой стороной квадрата, соответствующего узлу пересекается путь проводника. Он пересекается с верхней стороной. Соответственно следующий узел – четвертый (синяя стрелка). Поскольку узел не пуст, посмотрим в какой узел второго уровня попадет прямая. Поскольку она пересекает правый нижний угол, значит она попадет во второй подузел. Он пуст. Больше прямая не пересекает в этом узле никаких подузлов. Возвращаемся на первый уровень дерева и ищем следующий узел – это третий (зеленая стрелка). Поскольку узел не пуст, рассматриваем какие подузлы пересекает прямая. Поскольку она пересекает низ правой стороны квадрата узла, то первый узел второго уровня в который она попадет будет первым подузлом нашего узла. Этот подузел зеленый, значит, он содержит препятствие. Однако у него нет дочерних узлов, поэтому мы извлекаем координаты препетствия и ищем пересечение с нашей прямой. Пересечение есть. Следующим узлом будет четвертый, в нем мы тоже найдем пересечение с препятствием. И последним узлом будет третий – он свободен.

Опишите самостоятельно порядок обхода квадродерева для отрезка прямой, пересекающей участок кристалла перпендикулярно первой из левого верхнего угла в правый нижний.

Вопросы и задания для самостоятельной проработки:

1. Приведите примеры задач для которых удобно использовать разбиение пространства ([4]).

2. Приведите пример удачного и неудачного применения разбиения на сектора ([5]).

3. Приведите пример процедуры вставки в дерево двоичного разбиения пространства([2]).

4. Приведите пример трассировки луча в kd-дереве ([4]).

5. Сформулируйте достоинства и недостатки квадродеревьев. Приведите примеры ([6]).

6. Приведите пример процедуры поиска в R-дереве ([7]).

Список литературы:

1. R-Trees: A Dynamic Index Structure for Spatial Searching, Proc. 1984 ACM SIGMOD International Conference on Management of Data, pp. 47-57

2. Shevtsov M., Soupikov A., Kapustin A. Highly Parallel Fast KD-tree Construction for Interactive Ray Tracing of Dynamic Scenes. In Proceedings of the EUROGRAPHICS conference, 2007.

3. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Introduction to algorithms. — 2-е изд.

4. http://undergraduate.csse.uwa.edu.au/units/CITS4241/Handouts/Lecture14.html

5. http://www.drdobbs.com/article/print?articleId=184409694

6. http://www.cs.berkeley.edu/~demmel/cs267/lecture26/lecture26.html

7. http://www.rtreeportal.org/index.php?option=com_content&task=view&id=16&Itemid=31

Лекция 15 Экстремальные задачи физического синтеза. Линейное и нелинейное программирование. Алгоритмы имитационного моделирования. Муравьиный алгоритм. Алгоритм моделирования отжига. Силовые алгоритмы. Векторная трассировка свитчбокса.

Содержание:

1. Введение.

2. Математическое программирование.

3. Методы математической оптимизации.

4. Линейное и нелинейное программирование.

5. Муравьиный алгоритм.

6. Алгоритм имитации отжига.

7. Силовые методы.

Практически все задачи физического синтеза можно свести к нахождению экстремума некоей целевой функции. Однако зачастую такая функция дискретна, нелинейна или имеет разрывы. Поэтому для решения задач такого рода применяются нетрадиционные методы математической оптимизации.

Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Математическое программирование — дисциплина, изучающая теорию и методы решения задачи оптимизации.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

1. детерминированные;

2. случайные (стохастические);

3. комбинированные.

По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

1. прямые методы, требующие только вычислений целевой функции в точках приближений;

2. методы первого порядка: требуют вычисления первых частных производных функции;

3. методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Помимо того, оптимизационные методы делятся на следующие группы:

1. аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);

2. численные методы;

3. графические методы.

В зависимости от природы множества X задачи математического программирования классифицируются как:

1. задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;

2. задачи целочисленного программирования — если X является подмножеством множества целых чисел;

3. задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.

Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

1. Определение границ системы оптимизации

Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается

2. Выбор управляемых переменных

«Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)

3. Определение ограничений на управляемые переменные

Выбор числового критерия оптимизации (например, показателя эффективности)

4. Создаём целевую функцию

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

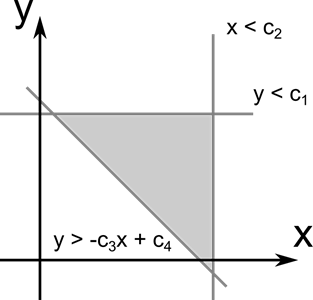
Рисунок 44. Задача линейного программирования

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.

Нелинейное программирование - раздел математического программирования, посвященный теории и методам решения задач оптимизации нелинейных функций на множествах, задаваемых нелинейными ограничениями (равенствами и неравенствами).

Основная трудность решения задач Н. п. состоит в том, что эти задачи являются многоэкстремальными, и известные численные методы их решения гарантируют в общем случае сходимость минимизирующих последовательностей лишь к точкам локальных экстремумов.

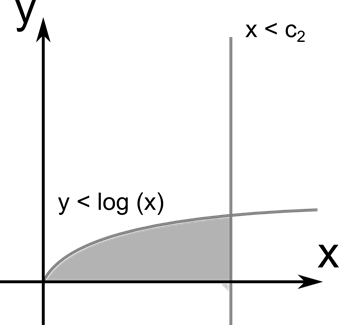
Рисунок 45. Задача нелинейного программирования

Наиболее изученным разделом Н. п. является выпуклое программирование, задачи которого характеризуются тем, что любая точка локального минимума является точкой глобального минимума.

Муравьиный алгоритм (алгоритм оптимизации подражанием муравьиной колонии, англ. ant colony optimization, ACO) — один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра, а также аналогичных задач поиска маршрутов на графах. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую (англ. metaheuristic, meta — «за пределами» и heuristic — «найти») оптимизацию. Первая версия алгоритма, предложенная доктором наук Марко Дориго в 1992 году, была направлена на поиск оптимального пути в графе.

В реальном мире, муравьи (первоначально) ходят в случайном порядке и по нахождению продовольствия возвращаются в свою колонию, прокладывая феромонами тропы. Если другие муравьи находят такие тропы, они, вероятнее всего, пойдут по ним. Вместо того, чтобы отслеживать цепочку, они укрепляют её при возвращении, если в конечном итоге находят источник питания. Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. На коротком пути, для сравнения, прохождение будет более быстрым и как следствие, плотность феромонов остаётся высокой. Испарение феромонов так же имеет свойство избежания, стремления к локально-оптимальн

Дата добавления: 2014-01-07