Лекция 9. Метод конечных элементов

Метод конечных элементов применяется во многих областях техники. Первоначально он служил для нахождения экстремумов в вариационном исчислении. Расчет электростатических полей строится на следующем положении – энергия поля в определенном объёме с заданными граничными условиями должна быть минимальной. Поскольку энергия поля в единичном объёме равна:

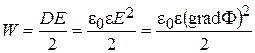,то (3.16)

функция F_W должна иметь минимум в объёме V между электродами. Функцию F_W называют энергетическим функционалом для определенного объёма V.

В ходе решения уравнения пространство разбивается на элементы, например, на треугольники для случая плоских полей или тетраэдры в случае трехмерного поля. Эти формы фигур позволяют в дальнейшем довольно просто проводить дробление сетки в областях с резкими изменениями поля. В пределах выбранного элемента для аппроксимации потенциала используются полиномы различной степени, например, для плоского поля:

Ф = а₀ +а₁х +а₂у (3.17)

В формуле (3.17) в качестве полинома использован полином первой степени. Изменение потенциала в пределах элемента выражается через координаты его вершин. Пусть у треугольника, показанного на рис.3.5а, с координатами м 1(1;1), м 2(2;3), м 3(3;1) потенциалы вершин известны: потенциал точки М 1 равен Ф1=11В, точки М 2 - Ф2=16В, точки М 3 - Ф3=13В (координаты на рис.3.5а приведены в сантиметрах). Подставив эти потенциалы в выражения (3.17), получим систему трех линейных уравнений с тремя неизвестными:

а ₀ + а ₁ х ₁ + а ₂ у ₁ = а ₀ + а ₁ + а ₂ =11

а ₀ + а ₁ х ₂ + а ₂ у ₂ = а ₀ +2 а ₁ +3 а ₂ =16

а ₀ + а ₁ х ₃ + а ₂ у ₃ = а ₀ +3 а ₁ + а ₂ =13

Система уравнений имеет следующее решение: а ₀ = 8 В, а ₁=1 В/см, а ₂=2В/см. Тогда в пределах площади треугольника рис.3.5а функция потенциала Ф будет иметь вид: Ф = (8+ х +2 у)В. Напряженность поля в пределах треугольника при линейной аппроксимации остается постоянной gradФ=(а ₁²+ а ₂²)^0,5. Для рассматриваемого примера напряженность в точках м 1, м 2 и м 3 равна Е = -gradФ = -В/см. Вклад в энергетический функционал от рассматриваемой точки, например точки м 1, при e = 1 будет равен: F¢_W = 1/2 e₀(gradФ₁)² = 5/2 e₀= 33.1×10^-12 Дж.

Вклад от элемента (треугольник) в энергетический функционал выражается интегралом по поверхности элемента. В расчетах этот поверхностный интеграл распространяется на всю поверхность рассчитываемого поля S. Для плоского поля энергетический функционал 3.16 принимает вид

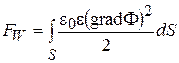(3.18)

Минимизация такого функционала в каждой точке сетки i осуществляется следующим образом – производная от функционала (3.18) по потенциалу в данной точке должна равняться нулю:

. (3.19)

Часть потенциалов Ф _i равна потенциалу электродов, а остальные неизвестные потенциалы можно рассчитать с помощью уравнений (3.18), (3.19). В этом методе, как и в дифференциальном методе, рассмотренном в предыдущем параграфе, должны быть известны все потенциалы по всей границе поля.

Принципиально решение проблемы нахождения параметров поля в методе конечных элементов сравнимо с непосредственным решением уравнения дифференциальным методом, причем области с различными диэлектрическими проницаемостями могут быть учтены непосредственно в уравнении (3.18). Существенным преимуществом метода конечных элементов является большая гибкость в построении сетки в пространстве поля, подлежащем расчету. Эта гибкость облегчает программную реализацию на ЭВМ. В настоящее время существуют развитые интегрированные пакеты прикладных программ для расчетов по методу конечных элементов, например ANSYS.

Ожидаемая точность вычислений в значительной степени зависит от вида функции, аппроксимирующей потенциал в каждом элементе. Для такой аппроксимации подходящими являются полиномы. Решение тем точнее, чем выше степень полинома. Вместе с ростом степени полинома существенно растет время расчета. Часто ограничиваются второй степенью полинома. На рис.3.5б и рис.3в приведены возможные полиномы при различном числе узловых точек элементов двумерного поля.

Для уменьшения погрешности расчетов в программу закладывают автоматическое изменение числа элементов в зависимости от степени неоднородности поля.

При расчетах полей электродов с плавающим потенциалом их заменяют диэлектриком с высокой диэлектрической проницаемостью. Для уменьшения погрешности, вызванной таким допущением, величину относительной диэлектрической проницаемости следует брать больше 10⁴ (e > 10⁴).

Расчет трехмерных полей методом конечных элементов является достаточно трудоемким, как, впрочем, и расчеты другими методами. Вместо треугольных элементов, использовавшихся в расчетах плоских полей, здесь элементом служит тетраэдр. Более сложный характер приобретает и закон изменения потенциала.

Дата добавления: 2014-01-07