Критерий устойчивости Михайлова. Из выражения (5.10) следует критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу

Из выражения (5.10) следует критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу вектора, записанному в виде

D(jw) = X(w) + jY(w) = D(w)e^jy(w) , (5.11)

где X(w) и Y(w) действительная и мнимая части характеристического вектора, а D(w) и y(w) его модуль и аргумент.

Формулировка критерия. Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(jw) при изменении w от 0 до ¥ равнялось бы n.

Другими словами, система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения системы.

На рис.5.8 приведены примеры годографов для устойчивой и неустойчивой систем.

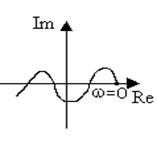
а) б)

Рис. 5.8. Кривая Михайлова:

а - устойчивой системы 3-го порядка; б - неустойчивой системы

Если годограф проходит через начало координат, то система находится на границе устойчивости. В этом случае

X(w) = 0 и Y(w) = 0. (5.12)

Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости.

Пример. Исследуем на устойчивость систему, рассмотренную в предыдущем примере, характеристический полином которой имеет вид: D(p) = T₁ T₂ p³ + (T₁ + T₂ )p² + p + k.

Решение. Найдем годограф характеристического вектора

D(jw) = T₁ T₂ (jw)³ + (T₁ + T₂ )(jw)² + jw + k.

Откуда

Re D(jw) = X(w) = k - (T₁ + T₂ )w²;

Im D(jw) = Y(w) = w - T₁ T₂ w³.

Для того, чтобы система 3-го порядка была устойчива, кривая Михайлова должна последовательно проходить три квадранта (рис.5.9).

Рис. 5.9. Кривая Михайлова

Найдем условие устойчивости из требования чередования корней

0=w₁<w₂<w₃.

Корень w₂ находится из уравнения X(w)=0, откуда

.

Отсюда первое условие устойчивости: k>0.

Корень w₃ находится из уравнения Y(w)=0, откуда

.

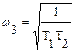Подставляя эти значения в требуемое условие w₂<w₃, получаем второе условие устойчивости системы

k < (+ ),

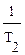которое, конечно, совпадает с полученным ранее условием устойчивости по критерию Гурвица.

Дата добавления: 2014-01-07