Полиномиальные коды

Представление кодового слова (n,k)-кода в виде последовательности U = (U₀, U₁,..., U_n-1) длиной n символов или их задание с помощью системы проверочных уравнений и порождающей матрицы не является единственно возможным. Еще один удобный и широко используемый способ представления того же кодового слова состоит в том, что элементы U₀, U₁,..., U_n-1 являются коэффициентами многочлена от X, то есть

U(х) = f(х) = U₀ +U₁× Х + U₂×Х² +...+U_{n- 1}×Х^n-1. (3.51)

Используя это представление, можно определить полиномиальный код как множество всех многочленов степени, не большей n -1, содержащих в качестве общего множителя некоторый фиксированный многочлен g(x).

Многочлен g(x) называется порождающим многочленом кода.

Представление кодовых слов в такой форме позволяет свести действия над комбинациями символов к действию над полиномами.

Определим действия над полиномами в поле двоичных символов GF(2).

Суммой двух полиномов f(x) и g(x) из GF(2) называется полином из GF(2), определяемый следующим образом:

f(x) + g(x) = 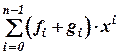. (3.52)

Другими словами, сложению двоичных полиномов соответствует сложение по mod2 коэффициентов при одинаковых степенях х.

₊ X³+X²+0×X+1 X+1

Х³ + Х² + Х+ 0 = Х³ + Х² + X, (3.53)

Например:

 

X³ + X² + 0×X + 1 X² + X + 1

X³ + 0 + X + 0 = X³ + X. (3.54)

Произведением двух полиномов из GF(2) называется полином из GF(2), определяемый следующим образом:

f(x)× g(x)= , (3.55)

то есть произведение получается по обычному правилу перемножения степенных функций, однако получаемые коэффициенты при данной степени Х складываются по модулю 2.

X³ + X² + 0 + 1 X + 1 X³ + X² + 0 + 1 X⁴ + X³ + 0 + X X⁴ + 0 + X² + X + 1 = X⁴ + X² + X +1, (3.56)

Например:

X ³ + X² + 0 + 1 X² + X X⁴ + X³ + 0 + X X⁵ + X ⁴ + 0 + X² X⁵ + 0 + X³ + X² + X = X⁵ + X³ + X² + X. (1.57)

Наконец, можно сформулировать теорему о делении полиномов: для каждой пары полиномов С(х) и d(x), d(x) ¹ 0 существует единственная пара полиномов q(x) — частное и r(х) — остаток, такие, что

С(х) = q(x)× d(x) + r(х), (3.58)

где степень остатка r(х) меньше степени делителя d(x).

Иными словами, деление полиномов производится по правилам деления степенных функций, при этом операция вычитания заменяется суммированием по mod2.

X³ + X² + X+ 1 X³ + X² X + 1

X + 1

0 ¬¾ остаток r(x). (3.59  

Например:

Еще раз напомним, что при сложении по mod2 сумма двух единиц (то есть двух элементов полинома с одинаковыми степенями) будет равна нулю, а не привычным в десятичной системе счисления двум. И, кроме этого, операции вычитания и сложения по mod2 совпадают.

Дата добавления: 2014-01-07