Многомерные плоскости

Пусть 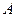– произвольная точка аффинного пространств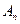а , а 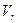- некоторое подпространство векторного пространства 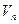, связанного с 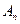(подпространство есть множество векторов, само являющееся пространством относительно заданных на исходном пространстве операций).

Определение 1: множество точек полученных при откладывании от точки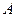

всех векторов подпространства 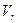называется r-мерной плоскостью, натянутой на точку 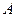и подпространство 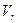и обозначается 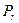. Подпространство 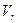называется направляющим подпространством плоскости .

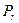Выберем в подпространстве 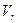какой – либо базис 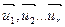, и будем говорить, что плоскость 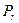натянута на точку 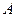и векторы 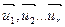. Тогда плоскость 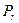можно определить как множество таких точек , что

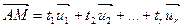, (1)

где коэффициенты (параметры) принимают независимо друг от друга всевозможные действительные значения.

Замечание 1: при 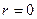подпространство - состоит только из нулевого вектора, а плоскость 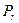- только из точки 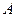. Поэтому любую точку будем рассматривать как нуль - мерную плоскостью

Определение 2: при имеем одномерную плоскость, которую назовем прямой и обозначим 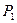. При 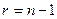получим - мерную плоскость, назовем ее гиперплоскостью и обозначим .

Замечание 2: если 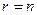, то получаем базис всего векторного пространства 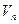, поэтому все пространство 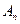можно считать n-мерной плоскостью.

Пример: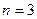, для пространства 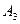введенные выше по определению понятия уже знакомы из школьного курса геометрии (они были там основными, неопределяемыми).

При прямая 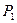задается уравнением:

,

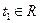
При 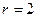двумерная плоскость 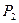, являющаяся гиперплоскостью пространства 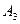(в школе она называлась просто плоскостью), задается уравнением:

, .

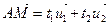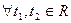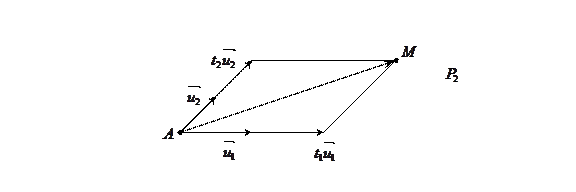
Определение 3: Множество точек из 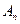таких, что равенство (1) выполняется при 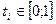, называется r – мерным параллелепипедом, натянутым на точку 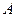и векторы .

Определение 4: одномерный параллелепипед называется отрезком и задается уравнением:

, .

Точк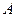и и 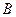, получаемые соответственно 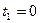при и при 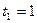, называются концами отрезка.

Если , то получаются внутренние точки отрезка .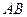

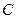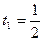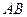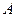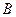Точка , получаемая при , называется серединой отрезка , а точки и называются симметричными относительно .

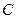Определение 5: число такое что 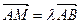, называется отношением, в котором точка делит отрезок .

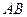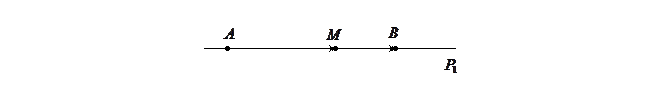
Для этого рисунка: .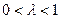

2º Плоскость как аффинное пространство

Роль точки 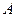в определении многомерной плоскости может играть любая другая точка этой плоскости.

Теорема 1: если плоскость 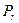натянута на точку 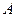и подпространство 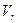, то она также натянута на это подпространство и любую другую свою точку .

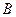□ Обозначим через 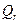плоскость натянутую на 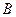и 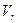. Требуется доказать, что 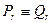, то есть что всякая точка, принадлежащая одной плоскости, принадлежит также и другой.

1) Пусть 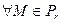, тогда . Так как , то и 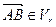. По аксиоме треугольника II имеем:

, то есть .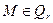

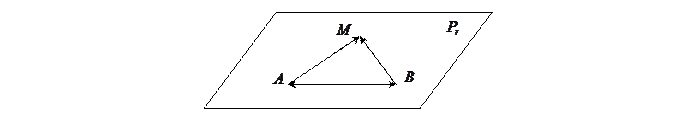
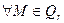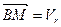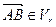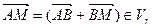2) Обратно, пусть , тогда . Так как , то , то есть . ■

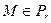Теорема 2: всякая r – мерная плоскость является r – мерным аффинным пространством.

□ Пусть 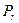- плоскость, натянутая в пространстве 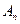на точку 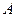и подпространство 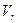. Выберем в 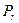две произвольные точки и , тогда и 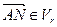, следовательно: .

Таким образом, каждой упорядоченной паре точек и плоскости 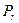соответствует определенный вектор ее направляющего подпространства 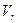. Из определения r – мерной плоскости и теоремы (1) следует, что для 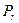выполняется аксиома I. Аксиома треугольника II, является справедливой для любых точек пространства 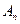, выполняется в частности и для плоскости . ■

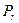§4. Способы задания многомерной плоскости

1º Векторные уравнения.

Пусть в пространстве 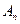плоскость 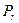натянута на точку 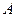и линейно независимые векторы 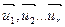. Тогда по определению она состоит из таких точек , что:

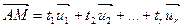, (1)

где , .

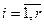Для трех точек 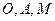из 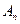по аксиоме треугольника II имеем:

или

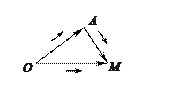
. (2)

Уравнения (1) и (2) называются векторными уравнениями плоскости .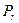

2º Параметрические уравнения.

Пусть в некоторой АСК 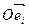точка имеет координаты 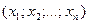, точка 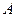имеет координаты 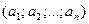, векторы 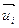имеют в базисе 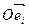следующие координаты:

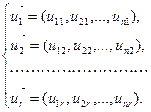
Тогда, подставляя соответствующие разложения векторов: , , , , 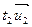…, 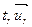в уравнение (2) и приравнивая в левой и правой частях коэффициенты при одинаковых координатных векторах, получаем систему линейных уравнений:

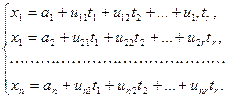(3)

Уравнения (3) выражают текущие координаты 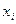точек плоскости 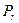с помощью линейных функций от 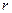параметров и называются параметрическими уравнениями этой плоскости. В случае для прямой 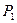имеем:

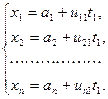
(4)

Исключив параметр , получаем:

(5)

При 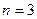имеем уже знакомые канонические уравнения прямой .

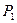3º Общие уравнения.

Исключить параметры 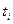из уравнения (3) можно и в случае плоскости любой размерности , .

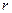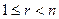Опишем этот прием.

1) Какие - либо 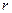уравнений из системы (3) разрешим относительно параметров , то есть выразим их через переменные . Это возможно, так как векторы 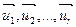линейно независимы, значит

.

Тогда хотя бы один минор этой матрицы порядка 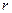отличен от нуля.

2) Подставим полученные выражения для 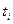в оставшиеся 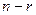уравнений, при

этом получим систему из 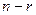уравнений с переменными 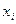(не обязательно всеми!), не содержащую параметров :

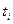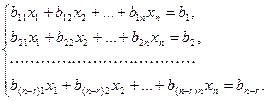(6)

Так как точка 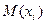принадлежит плоскости 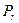тогда и только тогда, когда ее координаты удовлетворяют полученным уравнениям, то уравнения (6) называются общими уравнениями этой плоскости.

Итак, любая плоскость 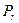, , 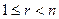в аффинном пространстве 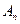может быть задана системой 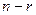линейных уравнений. В частности, для гиперплоскости : 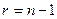, , 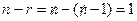то есть она может быть задана одним линейным уравнением.

Замечание 1: так как параметры можно исключить из системы (3) по-разному, то, то одна и та же плоскость 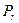, может задаваться различными системами линейных уравнений.

Замечание 2: перейти от системы вида (6) к уравнениям вида (3) и далее к уравнениям (2) и (1) можно в обратном порядке, например, положив: .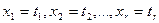

Пример: составить различные уравнения плоскости 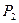, натянутой в аффинном пространстве 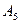на точку 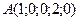и векторы , .

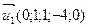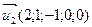Решение: Так как соответствующие координаты векторов 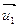и 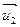не пропорциональны, то эти векторы не коллинеарны, следовательно, линейно независимы и являются направляющими векторами пространства , связанного с .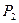

1) 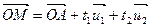, 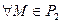- векторное уравнение.

2) - параметрические уравнения.

3) Из 2-го и 3-го уравнения выразим и : , .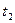

.

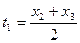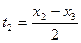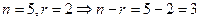Подставим эти выражения в оставшиеся три уравнения:

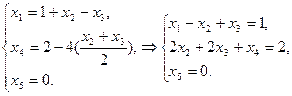- общие уравнения.

Другой способ исключения параметров и 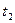дает другой результат:

, :

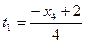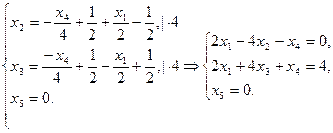
§5. Взаимное расположение многомерных плоскостей

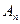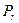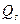Рассмотрим в аффинном пространстве две плоскости и , где 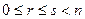, с направляющими подпространствами 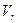и .

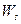Определение 1: плоскост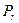и и 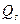называются параллельными, если направляющие подпространства одной из них (меньшей по размерности) содержится в направляющем подпространстве другой плоскости.

.

Определение 2: если плоскости P_r и Q_s не параллельны и имеют хотя бы одну точку, то они называются пересекающимися.

Определение 3: если плоскости P_r и Q_s не параллельны и не имеют общих точек, то они называются скрещивающимися.

Теорема 1: если две плоскости пересекаются, то их пересечение есть плоскость, направляющее подпространство которой является пересечением направляющих подпространств этих плоскостей. [3], §4, c.18, Т.1.

□ Пусть P_r натянута на точку А и подпространство V_r, а Q_s натянута на точку B и подпространство W_s. Пусть C P_r ∩ Q_s – их общая точка, обозначим V_r ∩ W_s = U_{p ,} а Т_р – плоскость, натянутую на C и U_p.

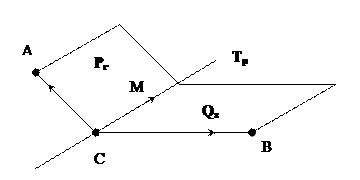
Докажем, что T_p = P_r ∩ Q_s.

1) Пусть MT_p, тогда U_p = V_r ∩ W_s, значит V_r и W_s, то есть M P_r и M Q_s, поэтому M P_r ∩ Q_s.

2) Обратно: если M P_r ∩ Q_s, то M P_r и M Q_s, откуда V_r и W_s, следовательно: U_p = V_r ∩ W_s, тогда MT_p. ■

Теорема 2: если две плоскости параллельны и пересекаются, то одна из них (меньшей размерности) принадлежит другой (большей размерности). [3], §4, c.19, Т.2.

□ Пусть P_r || Q_s и С = P_r ∩ Q_s, где для определенности r ≤ s. Тогда по определению параллельности V_r W_s. Докажем, что P_r Q_s, то есть что любая точка M P_r принадлежит также и Q_s.

Пусть M P_r, тогда V_r, но V_r W_s, значит W_s или M Q_s. ■

Пример 1: n = 3, A₃ – трехмерное аффинное пространство, r = 1, s = 2, прямая P₁ и двумерная плоскость Q₂.

1) P₁ || Q₂ и не имеют общих точек (в школьных учебниках - параллельны):

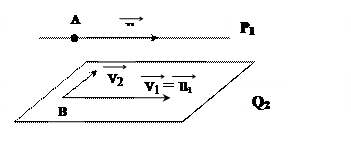
2) P₁ || Q₂ и имеют общие точки 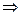P₁Q₂:

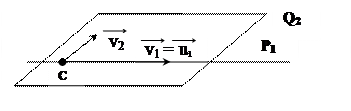
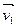В каждом из этих случаев V₁W₂, причем векторы и 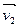базиса подпространства W₂ можно выбрать так, что вектор будет базисным вектором и для подпространства V₁.

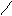3) P₁ || Q₂ 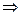они имеют единственную общую точку С, найти ее координаты можно, решив совместно уравнения, задающие прямую P₁ и плоскость Q₂.

Таким образом, в A₃ плоскости P₁ и Q₂ не могут скрещиваться (однако, в пространстве A₄ это возможно).

4) P₁ и Q₁, r = s = 1.

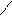
и 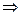P₁ · Q₂ – скрещиваются.

Заметим, что: .

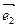
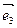
Пример 2: в пространстве A₅ исследовать взаимное расположение прямой P₁ – оси Ox аффинной системы координат 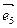– и плоскости Q₂, натянутой на точку B(-1;0;0;0;0) и векторы 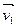(0;1;0;2;0) и

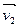(0;1;0;-1;1)

Решение: 1) Установим, параллельны ли P₁ и Q₂.

Прямая P₁ натянута на точку 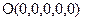и третий координатный вектор 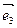==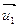(0;0;1;0;0). Найдем ранг матрицы из координат векторов , , :

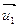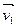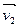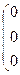
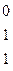
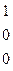
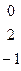
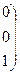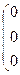
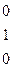
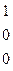
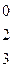
~ r=3 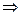векторы линейно независимы,

=2≠0

вектор 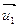не может быть линейной комбинацией векторов 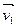и 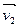значит V₁W₂ и P₁ || Q₂.

2) Установим, имеют ли эти плоскости общие точки, для чего решим совместно их параметрические уравнения:

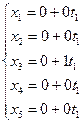P₁: , Q₂: .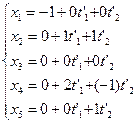

Сравним первые уравнения (x₁ = 0 и x₁ = -1), замечаем, что система несовместна, общих точек нет, плоскости P₁ и Q₂ скрещиваются:

P₁ · Q₂.

Замечание: имеет место теорема: для скрещивающихся плоскостей аффинного пространства сумма их размерностей меньше размерности пространства, то есть плоскости P_r и Q_s пространства 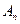не могут скрещиваться, если r + s ≥ n.

(Плоскости P_r и Q_s пространства 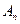могут скрещиваться тогда и только тогда, когда r + s < n. Если n>1, то гиперплоскости не могут скрещиваться).

Дата добавления: 2014-01-07