Предмет аффинной геометрии

Будем понимать под фигурами пространства 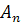некоторые множества точек этого пространства. Пусть аффинное преобразование f отображает фигуру F на фигуру F’: .

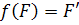Определение 5: свойства фигуры F, не меняющиеся при данном преобразовании f, называются инвариантными относительно этого преобразования. Свойства фигур, инвариантные относительно любых аффинных преобразований, называется аффинными свойствами.

Определение 6: аффинной геометрией называется наука, изучающая аффинные свойства (инварианты) фигур аффинного n – мерного действительного пространства .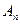

Примеры: 1) Любое аффинное преобразование отображает r – мерную плоскость также на r – мерную плоскость. Следовательно, свойства множества точек быть r – мерной плоскостью является аффинным и r – мерная плоскость есть понятие аффинной геометрии. Кроме того, параллельность плоскости также является аффинным свойством.

2) Аффинным являются также понятия линейной независимости векторов, простое отношение трёх точек прямой, аффинные координаты точки. Все доказанные выше теоремы выражают свойства этих понятий и являются теоремами многомерной аффинной геометрии.

Определение 7: фигура F₁ называется аффинно-эквивалентной фигуре F₁, если существует аффинное преобразование пространства 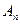, отображающая фигуру F₁ на фигуру F₂.

Замечание: в школьном курсе геометрии равные фигуры не отличаются друг от друга по своим свойствам. Аналогично с точки зрения аффинной геометрии все свойства аффинно-эквивалентных фигур одинаковы.

Теорема 3: любые две r – мерные плоскости аффинно- эквивалентны.

□ Пусть в пространстве 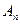плоскость Р_r натянута на точку А и векторы 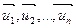, а плоскость Р'_r натянута на точку А' и векторы .

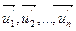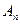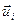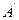
Допишем эти линейно независимые системы так, чтобы получить две аффинные системы координат пространства , А , , 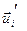где i = 1, 2,…,n. По теореме (3) из § 8 существует единственное аффинное преобразование, переводящее первый репер во второй. Тогда, в частности, А, 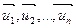, отображаются на А', 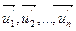, следовательно Р_r отображается на Р'_r, что означает их аффинную эквивалентность. ■

§ 10. Евклидово векторное пространство.

1º. Пусть имеется действительное n – мерное векторное пространство V_n, то есть непустое множество элементов, называемых векторами, в котором заданы операции сложения векторов и умножение вектора на число, удовлетворяющие 10 аксиомам 3 групп: I. – Аксиомы сложения векторов. II. – Аксиомы умножения вектора на число. III. – Аксиомы размерностей. Зададим ещё одну операцию скалярного умножения векторов: любым двум векторам 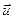и 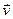сопоставим действительное число 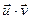– их скалярное произведение.

Определение 1: векторное пространство 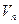называется n – мерным евклидовым векторным пространством, если скалярное произведение подчиняется аксиомам:

Дата добавления: 2014-01-07