
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Евклидово точечное и n – мерное пространства
|
|
|
|
Определение 1: аффинное пространство 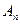 называется евклидовым точечным или просто евклидовым пространством, если связанное с ним пространство
называется евклидовым точечным или просто евклидовым пространством, если связанное с ним пространство 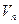 является евклидовым векторным пространством и обозначается
является евклидовым векторным пространством и обозначается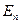 .
.
Замечание 1: точки и векторы являются основными объектами пространства 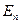 , а операции над ними называются основными или неопределяемыми отношениями. Природа основных объектов может быть любой, требуется лишь, чтобы основные отношения удовлетворяли аксиомам всех пяти групп. Все другие объекты и отношения определяются через основные, а при доказательствах теорем используются лишь аксиомы и ранее доказанные их следствия. Все определения и теоремы, сформулированные для пространства
, а операции над ними называются основными или неопределяемыми отношениями. Природа основных объектов может быть любой, требуется лишь, чтобы основные отношения удовлетворяли аксиомам всех пяти групп. Все другие объекты и отношения определяются через основные, а при доказательствах теорем используются лишь аксиомы и ранее доказанные их следствия. Все определения и теоремы, сформулированные для пространства 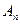 верны и для пространства
верны и для пространства 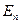 .
.
Определение 2: аффинная система координат в пространстве 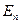 называется прямоугольной декартовой, если её координатные векторы
называется прямоугольной декартовой, если её координатные векторы 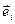 ,
, 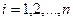 , образуют ортонормированный базис, связанного с ним евклидова векторного пространства
, образуют ортонормированный базис, связанного с ним евклидова векторного пространства 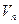 .
.
Теорема 1: при переходе от одной из двух прямоугольных декартовых систем координат к другой координаты 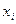 произвольной точки в старой системе выражаются через её координаты
произвольной точки в старой системе выражаются через её координаты 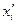 в новой системе координат формулами:
в новой системе координат формулами:
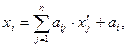
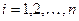 (1)
(1)
где 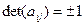 (то есть матрицы ортогональны).
(то есть матрицы ортогональны).
Эта теорема следует из теоремы (2) §2 и теоремы (3) §10, коэффициенты 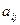 и
и 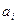 имеют прежний геометрический смысл.
имеют прежний геометрический смысл.
Пример 2: n=2, 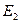 – евклидово пространство, формулы перехода известны из аналитической геометрии и являются частным случаем формул (1):
– евклидово пространство, формулы перехода известны из аналитической геометрии и являются частным случаем формул (1):

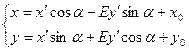 ,
, 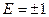 ,
,
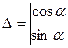
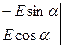 =
=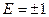 .
.
Определение 3: расстоянием от точки 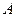 до точки
до точки 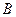 пространства
пространства 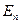 называется длина вектора
называется длина вектора 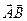 и обозначается
и обозначается 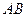 .
.
Пусть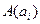 ,
,  в одной из прямоугольных декартовых систем координат
в одной из прямоугольных декартовых систем координат 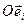 , тогда, очевидно:
, тогда, очевидно:
|
|
|
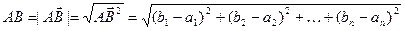
Теорема 2: для любых трёх точек 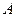 ,
, 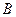 и
и 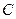 справедливо неравенство треугольника:
справедливо неравенство треугольника:
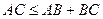 (2)
(2)
□ По аксиоме треугольника из параграфа §1 имеем: 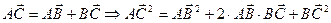 или
или 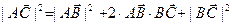 .
.
Так как 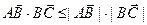 (при
(при 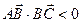 это очевидно, а при
это очевидно, а при 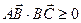 следует из неравенства Коши – Буняковского, замечание (1), §10), то
следует из неравенства Коши – Буняковского, замечание (1), §10), то
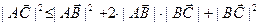 ,
, 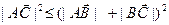 ,
, 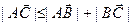 то есть
то есть 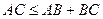 . ■
. ■
Замечание 2: очевидно, если 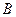 совпадает с
совпадает с 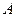 или
или 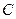 , то в формуле (2) имеет место знак равенства. Если же
, то в формуле (2) имеет место знак равенства. Если же 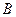 не совпадает ни с
не совпадает ни с 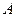 , ни с
, ни с 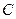 , то равенство выполняется тогда и только тогда, когда
, то равенство выполняется тогда и только тогда, когда 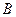 лежит на прямой
лежит на прямой 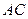 между точками
между точками 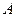 и
и 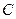 .
.
Определение 4: множество точек пространства 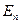 , расстояния от которых до данной точки
, расстояния от которых до данной точки 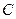 равны
равны 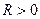 , называется гиперсферой с центром
, называется гиперсферой с центром 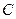 и радиусом
и радиусом 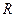 .
.
Если 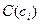 , а
, а 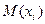 - точка гиперсферы, то имеем
- точка гиперсферы, то имеем 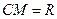 и
и
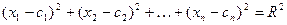 (3)
(3)
Определение 5: множество точек пространства 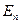 , расстояния от которых до данной точки
, расстояния от которых до данной точки 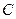 не превышает
не превышает 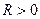 , называется n – мерным шаром. Очевидно, n – мерный шар задаётся в пространстве
, называется n – мерным шаром. Очевидно, n – мерный шар задаётся в пространстве 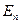 неравенством:
неравенством:
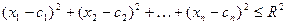 (4)
(4)
Примеры (частные случаи):
 1) n = 1,
1) n = 1, 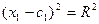

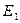 - прямая,
- прямая, 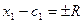
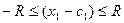
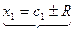
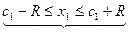
пара точек отрезок длины 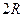

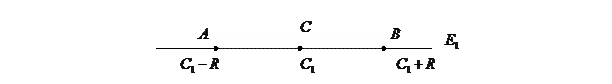
2) n = 2, E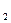 - плоскость:
- плоскость:
(x - c
- c )
)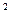 + (x
+ (x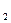 - c
- c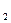 )
)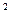 = R
= R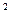 - окружность (x
- окружность (x - c
- c )
)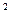 + (x
+ (x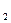 - c
- c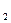 )
)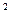
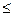 R
R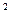 - круг
- круг
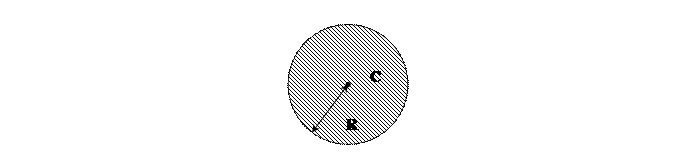
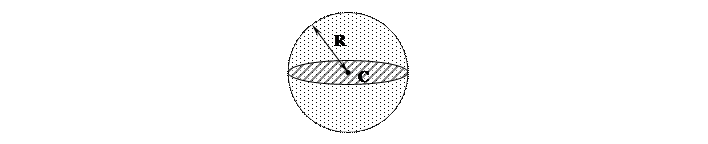
3) n=3, E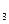 :
:
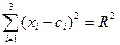 - сфера
- сфера 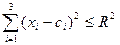 - шар
- шар
Определение 6: r-мерный параллелепипед пространства E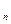 называется r-мерный кубом, если он натянут на точку А и единичные попарно ортогональные векторы:
называется r-мерный кубом, если он натянут на точку А и единичные попарно ортогональные векторы:
 = t
= t
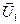 + t
+ t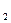
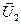 +…+ t
+…+ t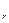
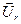 , 1
, 1 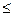 r
r 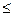 n,
n,
0 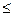 t
t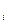
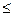 1, i =1,2,3,…r,
1, i =1,2,3,…r,  M
M 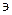 E
E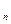 ,
, 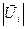 =1,
=1, 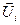
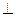
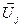 , i
, i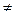 j.
j.
Примеры (частные случаи):
1) r =1 - отрезок длины 1:
A 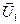 B AB=1
B AB=1

2) r = 2 - квадрат со стороной 1:

 .
.
3) r =8 – куб с ребром 1:
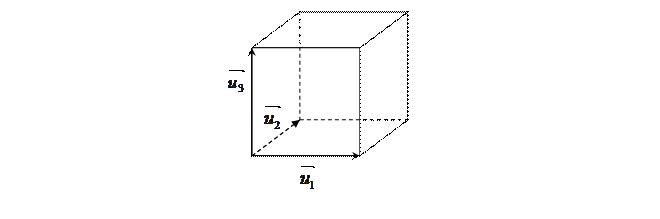
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2029; Нарушение авторских прав?; Мы поможем в написании вашей работы!