Просмотр дерева двоичного поиска

BinTreeSearch(Arrаy, v):

1. if a=l(v) then return "1" else

2. if а<l(v) then

3. if v имеет левого сына w then return BinTreeSearch(Arrаy, w)

4. else return "0" else

5. if v имеет правого сына w then return BinTreeSearch(Arrаy, w)

6. else return "0"

Деревья двоичного поиска также удобны для выполнения операций MIN и УДАЛИТЬ. Для нахождения наименьшего элемента в дереве двоичного поиска Т просматривается путь v ₀, v ₁ ,¼, v _p, где v ₀ – корень дерева T, v _i – левый сын узла v _i-1, l £ i £ p, и у узла v _p нет левого сына. Метка в узле v _p является наименьшим элементом в T. В некоторых задачах может оказаться удобным иметь указатель на v _p, чтобы обеспечить доступ к наименьшему элементу за постоянное время.

Реализовать операцию Delete (a, S) немного труднее. Допустим, что элемент а, подлежащий удалению, расположен в узле v. Возможны три случая:

1) v — лист; в этом случае v удаляется из дерева;

2) у v в точности один сын; в этом случае делаем отца узла v отцом его сына, тем самым удаляя v из дерева (если v – корень, то его сына делаем новым корнем);

3) у v два сына; в этом случае находим в левом поддереве узла v наибольший элемент b, рекурсивно удаляем из этого поддерева узел, содержащий b, и метим узел v элементом b. (Заметим, что среди элементов", меньших а, b будет наибольшим элементом всего дерева.)

Пример 3.3. На рис. 15 иллюстрируется пример удаления узла из бинарного дерева поиска. Предположим, что надо удалить узел 25 из данного дерева. Он расположен в корне, у которого два сына. Наибольшее число, меньшее 25, расположенное в левом поддереве корня,– это 15. Удаляем из дерева узел с меткой 15 и заменяем 25 на 15 в корне. Полученное дерево показано на рис. б. ÿ

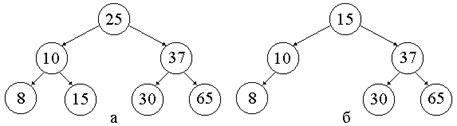
Рис. 15: Дерево двоичного поиска до (а) и после (б) выполнения операции УДАЛИТЬ (узел 25).

В качестве упражнения предлагаем написать программу на C++ для операции УДАЛИТЬ. Заметим, что одно выполнение любой из операций ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ, УДАЛИТЬ и MIN можно осуществить за время О (п),

Подсчитаем временнýю сложность последовательности из п операций ВСТАВИТЬ, когда рассматриваемое множество представлено деревом двоичного поиска. Время, требуемое, чтобы в дерево двоичного поиска вставить элемент a, ограничено по порядку числом сравнений, производимых между а и элементами, уже находящимися в дереве. Поэтому время можно измерять числом производимых сравнений.

В худшем случае добавление к дереву п элементов может потребовать квадратичного времени. Например, допустим, что последовательность элементов, которые надлежит добавить, оказалась упорядоченной (в порядке возрастания). Тогда дерево поиска будет просто цепью правых сыновей. Но если вставляется п случайных элементов, то, как показывает следующая теорема, вставка потребует время 0 (п log п).

Теорема 11. Среднее число сравнений, необходимых для вставка п случайных элементов в дерево двоичного поиска, пустое вначале, равно O(n log n) для n³ 1.

Доказательство. Пусть Т (п) – число сравнений, производимых между элементами последовательности a ₁, a ₂,¼, a _n при построении дерева двоичного поиска, T (0)= 0. Пусть b ₁, b ₂,¼, b _n – та же последовательность в порядке возрастания.

Если a ₁, a ₂,¼, a _n – случайная последовательность элементов, то a ₁ с равной вероятностью совпадает с b _j для любого j, 1 £ j £ n. Элемент a _i становится корнем дерева двоичного поиска, и в окончательном дереве j–1 элементов b ₁, b ₂,¼, b _j-1 будут находиться в левом поддереве корня и п–j элементов b _j+1, b _j+2,¼, b _n – в правом поддереве.

Подсчитаем среднее число сравнений, необходимых для вставки элементов b ₁, b ₂,¼, b _j-1 в дерево. Каждый из этих элементов когда-нибудь сравнивается с корнем, и это дает j–1 сравнений с корнем. Затем по индукции получаем, что еще потребуется Т (j–1) сравнений, чтобы вставить b ₁, b ₂,¼, b _j-1 в левое поддерево. Итак, необходимо j–1 + T (j–1) сравнений, чтобы вставить b ₁, b ₂,¼, b _j-1 в дерево двоичного поиска. Аналогично п–j+Т (п–j) сравнений потребуется, чтобы вставить в дерево элементы b _j+1, b _j+2,¼, b _n.

Поскольку j с равной вероятностью принимает любое значение от 1 до n, то

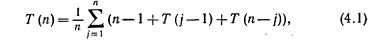
или, с учетом простых алгебраических преобразований,

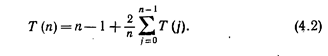
Способом, описанным в разделе 2.4, можно показать, что

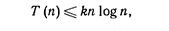
где k = ln 4 = 1,39. Таким образом, в среднем на вставку п элементов в дерево двоичного поиска тратится 0(п log п) сравнений. ÿ

Итак, методами этого раздела можно выполнить случайную последовательность из п операций ВСТАВИТЬ, УДАЛИТЬ, ПРИНАДЛЕЖАТЬ и MIN за среднее время О (п log п). Выполнение в худшем случае занимает квадратичное время. Однако даже это худшее время можно улучшить до О (п log п) с помощью одной из схем сбалансированных деревьев, которые обсуждаются далее.

3.5. Оптимальные деревья двоичного поиска

В разд. 4.3 по данному множеству S={ a ₁, a ₂,¼, a _n}, являющемуся подмножеством некоторого большого универсального множества U, строилась структура данных, позволяющая эффективно выполнить последовательность s, составленную только из операций ПРИНАДЛЕЖАТЬ. Рассмотрим снова эту задачу, но теперь предположим, что кроме множества S задается для каждого а Î U вероятность появления в s операции Member (a, S). Теперь желательно построить дерево двоичного поиска для S так, чтобы последовательность s операций ПРИНАДЛЕЖАТЬ можно было выполнить в префиксном режиме с наименьшим средним числом сравнений.

Пусть a ₁, a ₂,¼, a _n –элементы множества S в порядке возрастания и p _i – вероятность появления в s операции Member (a, S). Пусть q ₀ – вероятность появления в s операции Member (a, S) для некоторого а < a _i, а q _i – вероятность появления в s операции Member (a, S) для некоторого а, а _i < a < а _i+1. Наконец, пусть q _n – вероятность появленияв s операции Member (a, S) для некоторого а>а _n. Для определения стоимости дерева двоичного поиска удобно добавить к нему n+1 фиктивных листьев, чтобы отразить элементы из U–S. Эти листья будут обозначаться числами 0, 1, ¼, п.

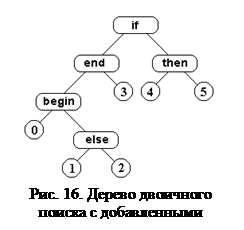На рис. 16 показано дерево двоичного поиска, изображенное на рис. 13, с добавленными фиктивными листьями. Например, лист с меткой 3 представляет те элементы а, для которых end < a < if.

Требуется определить стоимость дерева двоичного поиска. Если элемент а равен метке l (v) некоторого узла v, то число узлов, посещенных во время выполнения операции Member (a, S), на единицу больше глубины узла v. Если a Ï S и a _i< a < а _i+1, то число узлов, посещенных при выполнении операции Member (a, S), равно глубине фиктивного листа i. Поэтому стоимость дерева двоичного поиска можно определить как

,

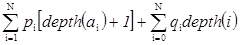где depth (¼) – глубина соответствующего узла дерева.

Теперь, если есть дерево двоичного поиска Т, обладающее наименьшей стоимостью, можно выполнить последовательность операций ПРИНАДЛЕЖАТЬ с наименьшим средним числом посещений узлов, просто применив для выполнения каждой операции ПРИНАДЛЕЖАТЬ алгоритм 14 на T.

Если даны числа p _i и q _i, то как найти дерево наименьшей стоимости? Подход "разделяй и властвуй" предлагает определить элемент a _i, который надо поставить в корень. Это разбило бы данную задачу на две подзадачи: построение левого и правого поддеревьев. Однако, похоже, нет легкого пути определения корня без решения всей задачи. Поэтому придется решать 2п подзадач: по две для каждого возможного корня. Это естественно приводит к решению с помощью динамического программирования.

Для 0 £ i < j £ n обозначим через Т _ij дерево наименьшей стоимости для подмножества { a _i+1, a _i+2, ¼, a _j}. Пусть c _ij – стоимость дерева Т _ij, а r _ij – его корень. Вес w _ij дерева Т _ij определяется как q _i + (p _i+1 + q _i+1)+ ¼ +(p _j + q _j).

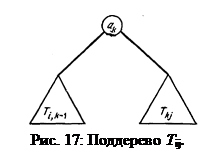
Дерево T _ij состоит из корня a _k, левого поддерева Т _i,k–1 (т. е. дерева наименьшей стоимости для { a _i+1, a _i+2, ¼, a _k–1}) и правого Т _kj (т. е. дерева наименьшей стоимости для { a _k+1, a _k+2, ¼, a _j}) (рис. 17). Если i=k–1, то нет левого поддерева, а при k=j нет правого поддерева. Для удобства Т _ii будет трактоваться как пустое дерево. Вес w _ii дерева Т _ii равен q _i, а его стоимость c _ii равна 0.

В Т _ij, i<j, глубина каждого узла в левом и правом поддеревьях на единицу больше глубины того же узла в Т _i,k–1 или Т _kj. Поэтому стоимость c _ij дерева Т _ij можно выразить так:

c _ij= w _i,k–1+ p _k+ w _kj+ c _i,k–1+ c _kj = w _ij + c _i,k–1+ c _kj.

Следует брать здесь то значение k, которое минимизирует сумму c _i,k–1+ c _kj. Поэтому для нахождения оптимального дерева Т _ij вычисляют для каждого k, i < k £ j, стоимость дерева с корнем a _k, левым поддеревом Т _i,k–1, и правым поддеревом Т _kj, а затем выбирают дерево наименьшей стоимости. Приведем соответствующий алгоритм.

Алгоритм 15. Построение оптимального дерева двоичного поиска

Вход. Множество S вида { a ₁, a ₂, ¼, a _n}, где a ₁ <a ₂ <¼<.a _n Известны также вероятности q ₀, q ₁ ,¼, q _n и p ₁ ,¼, p _n, где q _i, 1 £ i<n, – вероятность выполнения операции Member (a, S) для a _i <a<a _i+1, q ₀ – вероятность выполнения операции Member (a, S) для а<а ₁, q _n – вероятность выполнения операции Member (a, S) для a > a _n, a p _i, 1 £ i £ n, – вероятность выполнения операции Member (a, S).

Выход. Дерево двоичного поиска для S, обладающее наименьшей стоимостью.

Метод.

1. Для 0 £ i < j £ n вычисляются r _ij и c _ij в порядке возрастания разности j – i с помощью алгоритма динамического программирования.

Дата добавления: 2014-01-07