Лекция 29

ПОСТРОЕНИЕ ВЕРОЯТНОСТНОЙ БУМАГИ

Вид функции распределения устанавливают и графическим методом, нанося полученные экспериментальные данные на вероятностную бумагу. Графический способ проверки гипотез с помощью вероятностной бумаги был разработан в 1914 г. американским инженером А. Хозеном.

Суть построения состоит в следующем. На вероятностной бумаге в прямоугольной систем координат по оси ординат наносят шкалу, соответствующую функции закона распределения (нормальное распределение, экспоненциальное, распределение Вейбулла и т. д.), а по оси абсцисс — линейную или логарифмическую шкалу.

Основная идея графического метода состоит в том, что подбирают такую непрерывную замену координат, при которой график функции распределения становится прямой линией.

При построении вероятностных бумаг необходимо строить шкалы для функции распределения F(t). Эти шкалы, как правило, являются неравномерными. При построении вероятностных бумаг для нормального и экспоненциального распределений шкала случайного аргумента не подвергается преобразованиям — она остается равномерной; для распределений Вейбулла и логарифмически нормального распределения случайный аргумент подвергается логарифмическому преобразованию.

Вероятностные бумаги используют для решения двух задач.

Во-первых, для проверки согласия эмпирического распределения, с теоретическим. В этом случае полученные результаты испытаний в виде точек располагаются на вероятностной бумаге близко к прямой линии. Это свидетельствует о согласии опытных данных с тем законом распределения, для которого построена вероятностная бумага.

Во-вторых, с помощью вероятностной бумаги можно определить оценки параметров распределения по углу наклона прямой и по отрезкам, которые она отсекает на осях координат.

Для случая распределения по нормальному закону: F(t) = 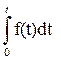и Р(t) =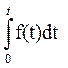=1 - F(t), а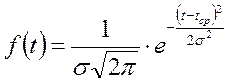

Заменим переменные величины 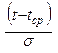= х =U, где U – квантиль нормального распределения, t_ср и σ - параметры распределения, а х = 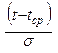- уравнение прямой

Если величину среднего квадратичного отклонения σ положить равной 1, то получим новую центрированную и нормированную функцию, плотность вероятности распределения которой

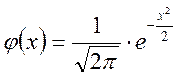
Данная функция табулирована

Вероятностную бумагу для нормального распределения строят следующим образом.

На оси абсцисс откладывают равно мерную шкалу для аргумента t, а по оси ординат — значения квантили U и надписывают величину F(t) (поэтому шкала на оси ординат получается неравномерной). Область изменения аргумен- та t определяет разность Δt = t_мах - t_мин

Пусть ширина графика равна L (измеряется в миллиметрах). Тогда значения t на оси абсцисс следует откладывать при помощи соотношения

S_t=k_t·t,

где k_t = L / Δt

Для построения шкалы функции F(t) распределения зададимся интервалом F_мин = 0.001 и F_мах = 0,999. Тогда (см. табл. 1 приложения) для U наименьшее значение будет —3,09 и наибольшее +3,09. Поэтому уравнение для S_F при длине шкалы L =160 мм записывается в следующем виде:

S_F = 160 ·U/(3,09 – (- 3,09))= 25,8 U

При F(t) < 0,5 пользуются соотношением

S_F = - S_{1 - F}

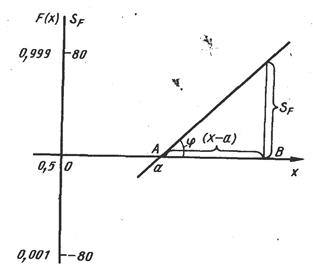
На рис. показана схема построения графика функции распределения на вероятностной бумаге.

Рис. График функции нормального распределения на вероятностной бумаге

Прямая пересекает ось t (х) в точке а [ это следует из уравнения 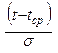= х =U ], так как при F(t) =0,5

U = 0.

Для определения σ воспользуемся уравнениями, из которых следует

σ = (t - t_ср)/U =(t - t_ср)25,8/k_t S_F,

Из этого уравнения и рис.

σ =25,8·ctgφ/ k_t

Величина k_t известна, а ctgφ легко найти по графику.

Построение вероятностной бумаги для экспоненциального закона распределения сводится к следующему.

Прологарифмируем уравнение функции распределения вида

F(t) = 1 – е ^{- λ t}

Результаты логарифмирования

—ln[1 — F(t)]= λt.

Из этого следует, что уравнение функции — линейная зависимость от t. Поэтому при построении вероятностной бумаги с использованием экспоненциального закона распределения по оси абсцисс для аргумента t откладывают равномерную шкалу, по оси ординат для функции F(t) — значения логарифмической функции —ln[1 — F(t)]. В результате получают неравномерную шкалу по оси ординат. Минимальное значение F(t) =0, максимальное значение F(t) =0,999. В этом случае наибольшее значение —ln[1 — F(t)] =6,908. Поэтом уравнение для S_F можно записать в следующем виде

S_F = —ln[1 — F(t)] · 160 / 6,908 = —23,2 ln[1 — F(t)]

Для построения шкалы t случайного аргумента можно воспользоваться уравнением S_t=k_t·t. Схема построения график функции экспоненциального распределения показана на рис.

Рис. График функции экспоненциального распределения на вероятностной бумаге

С учетом уравнений параметр λ находят, используя выражение

λ =—ln[1 — F(t)]/t = S_F k_t / 23,2 S_t = k_t tgφ / 23,2

При построении вероятностной бумаги для закона распределения Вейбулла прологарифмируем дважды уравнение функции распределения и в результате получим

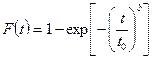- функция распределения Вейбулла,

= 1 - F(t),

ln{ - ln [1 - F(t)]} =bln = 2,303b(lgt – lgt₀) = 2,303b lg t –2,303b lg t₀;

ln{ - ln [1 - F(t)]} = y; lg t =x; –2,303b lg t₀ =C,

тогда получаем уравнение – y = 2,303х + С, откуда следует, что величина у линейно зависит от х.

Поэтому вероятностную бумагу строят так:

на оси абсцисс (горизонтальная ось) откладывают логарифмическую шкалу по уравнению

S_t=k_t·t

где k_t — масштабный фактор.

На оси ординат откладываем у, но проставляем у оси функцию F(t). Принимая 0,001≤ F(t)≤ 0,999, находим у_мин = - 6,91 и у_мах = 1,93, т. е. размах величины у равен 8,84. Поэтому уравнение для S_F можно записать следующим образом: S_F =160 · у/8,84 ≈ 18у

Необходимо знать, что при F(t)<0,6321 S_F < 0 и, наоборот, при F(t) > 0,6321 S_F >0

Схема построения графика функции распределения Вейбулла показана на рис.

Рис. График функции закона распределения Вейбулла на вероятностной бумаге.

Из уравнения у= 2,303b(lgt – lgt₀) следует, что у=0 при t = t₀. Поэтому величину х=а (см. график) находят в точке пересечения прямой с осью абсцисс.

Для нахождения значения b предположим, что в уравнении у= 2,303b(lgt – lgt₀) t=1. Тогда

у = – 2,303b lg t₀ =С

Из уравнения S_F =160·у/8,84 ≈ 18у длина отрезка А = - 18у( см.рис ) для точки t = t₀ (х=а) из уравнения S_t=k_t·t получим

S_а=k_t·lgt

Далее находим величину

b =А k_t /18·2,303S_А =k_ttgφ/41,45.

Для логарифмически нормального закона распределения 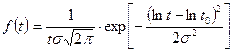уравнение прямой (рис.) выглядит так:

U =

График функции логарифмически нормального распределения приведен на рис.

Рис. График функции логарифмически нормального распределения на вероятностной бумаге

Схема построения пря-молинейного графика состоит в следующем. На вертикальной оси откладывают зна-чения S_F, вычисленные по формуле

S_F =k_FU

На горизонтальной оси откладывают значения S_t, вычисленные по формуле

S_t = k_t lgt

В точке пересечения прямой линии с осью абсцисс t =t₀ (х=а), т. е:

S_t=t0 = k_t lgt В точке пересечения прямой линии с осью ординат

t (х)= 1; S^'_F = k_FU = k_F lgt /σ

Из уравнения следует

σ = ctgα k_F / k_t

Таким образом, значения α просто вычисляют, используя ось абсцисс, а σ находят. при помощи графика и уравнения.

Логарифмическую шкалу по горизонтальной оси строят, используя уравнение вида

S_t = 100 lgt

При изменении значения— t (х)-от 1 до 10 длина шкалы L = 100 мм. Для значений аргумента t от 10 до 100 рассматривают величину 10 t, где t находится в пределах от 1 д0 10. Тогда в соответствии с уравнением имеем

S'_10t = 100lg10t = 100lg10t +100lgt = 100+ S_t

Аналогично получаем соотношения

S_100t = 200+ S_t; S_1000t = 300+ S_t

Дата добавления: 2014-01-07