Построение уравнения регрессии

В большинстве случаев при изучении взаимосвязей статистических признаков выбирают в качестве спецификации корреляционной модели линейные или внутренне линейные уравнения регрессии. Для определения их параметров используют метод наименьших квадратов. При этом решают задачу минимизации вида

.

В целевой функции 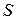параметр 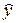заменяют конкретным уравнением регрессии и находят оптимальные значения параметров , , … , исходя из равенства нулю ее частных производных целевой функции по этим параметрам:

,

где частная производная целевой функции 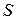по параметру .

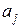Например, в случае парной линейной корреляции решают задачу минимизации

.

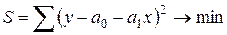При этом решение задачи сводится к решению системы уравнений

.

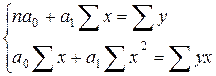Посредством несложных математических преобразований можно доказать, что между параметрами линейного уравнения парной регрессии и парным коэффициентом корреляции существует связь:

;

.

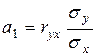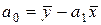Очевидно, что чем больше факторов в искомом уравнении, тем больше размерность решаемой системы. В общем случае при определении параметров 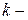факторного линейного уравнения регрессии необходимо решить систему, состоящую из 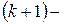го уравнения:

.

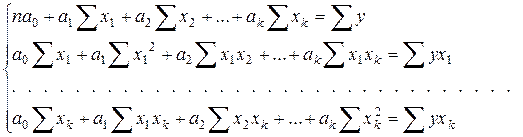Решение этой системы может быть осуществлено с использованием операций матричной алгебры:

при ,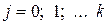

где:

определитель системы;

;

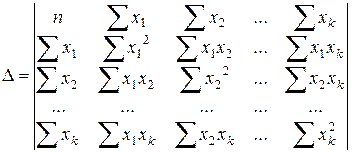частный определитель.

Матрицу для расчета частного определителя 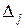получают из матрицы системы путем замены соответствующего столбца данными правой части уравнений системы.

После определения параметров уравнения регрессии приступают к оценке его адекватности фактическим данным. Вначале оценивают значимость факторных параметров уравнения по критерию Стьюдента

.

При выполнении этого условия факторный параметр признают значимым с вероятностью .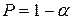

Фактически, значимость существенности отобранного фактора равносильна значимости соответствующего факторного параметра регрессии. Если отбор факторов по критерию существенности не проводился, то может оказаться, что выражение, стоящее в расчетной формуле, меньше нуля. Это говорит о том, что рассматриваемый фактор искажает корреляционную зависимость (его включение приводит к ослаблению зависимости результат от всех факторов в целом) и должен быть исключен из регрессионного уравнения.

В целом адекватность линейного уравнения множественной регрессии оценивают по тому же критерию, что и значимость множественного коэффициента корреляции:

.

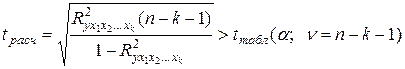При наличии только одного фактора (в случае парной регрессии) оценку значимости факторного параметра и адекватности уравнения в целом осуществляют на основе одного и того же критерия

.

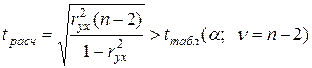Таким образом, значимость высокого значения парного коэффициента корреляции автоматически означает значимость факторного параметра парной линейной регрессии и адекватность ее уравнения фактическим значениям результативного признака.

Адекватность уравнения регрессии фактическим значениям результативного признака является основанием для применения этого уравнения на практике. При этом возможны следующие варианты вывода о практическом применении:

· если уравнение адекватно и одновременно значимы все его факторные параметры, то оно может применяться на практике как для принятия управленческих решений, так и для прогнозирования значений результативного признака;

· если уравнение адекватно, но хотя бы одни из факторных параметров не значим, то оно может быть применено только для принятия управленческих решений;

· если уравнение адекватно, но все факторные параметры не значимы, то уравнение не может применяться на практике по причине недостоверной оценки влияния на результат всех факторов.

Наглядной характеристикой адекватности уравнения регрессии любой спецификации является среднеквадратичная ошибка уравнения регрессии, рассчитываемая с учетом числа факторов:

.

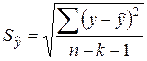Принято считать, что уравнение регрессии описывает фактические данные с высокой точностью, когда выполняется критерий

.

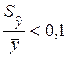Если поочередно один из факторов уравнения регрессии оставить в качестве переменной, а остальные факторы зафиксировать на среднем уровне, то получим частные уравнения регрессии, аналитически описывающие индивидуальное влияние факторов на результат.

В случае линейной регрессии частные уравнения имеют вид:

;

;

...........................

.

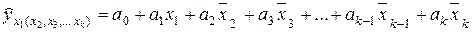После суммирования всех постоянных величин эти уравнения принимают вид линейных уравнений парной регрессии:

;

;

...........

.

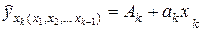После оценки адекватности уравнение регрессии экономически интерпретируют в части, касающейся его факторных параметров. При этом для каждого из факторов рассчитывают значения коэффициента эластичности

,

где первая производная функции, описывающей корреляцию, по фактору .

Коэффициент эластичности показывает, на сколько процентов и в какую сторону изменится результат из-за увеличения значения отдельного фактора на один процент при условии неизменности значений остальных факторов.

При линейной регрессии формула коэффициента эластичности имеет вид

.

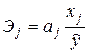Очевидно, что в общем случае значение коэффициента эластичности зависит от величины фактора, поэтому чтобы оценить эластичность индивидуального влияния фактора на результат на всем множестве факторных значений, рассчитывают среднюю величину коэффициента эластичности. В случае линейной регрессии средний коэффициент эластичности определяют по формуле

.

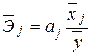Параметр в уравнении регрессии любого вида характеризует совместное влияние неучтенных факторов на результат. Как правило, значения этого параметра, особенно отрицательные, экономически не интерпретируют, так как это может привести к абсурдному выводу. Например, если в качестве результата рассматривается товарооборот предприятия, а в качестве фактора – физический объем продаж, то отрицательное значение будет означать, что при отсутствии продаж товарооборот принимает отрицательное значение, чего в принципе быть не может. Однако если в качестве результата рассматривается прибыль или ущерб от реализации продукции, то отрицательное значение может быть интерпретировано как величина ущерба при полном отсутствии реализации.

Пример 9.5. Вернемся к результатам, полученным в примере 9.1. Определим уравнение регрессии, описывающее корреляционную зависимость балансовой прибыли предприятия от объема реализованной им продукции, оценим его адекватность и проведем экономическую интерпретацию.

Решение.

Согласно эмпирической кривой (рис. 9.1) исследуемая зависимость является корреляционной и линейной. При оценке ее тесноты были получены следующие результаты:

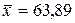млн. руб., 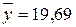млн. руб.;

млн. руб.; 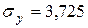млн. руб.;

.

Отсюда:

;

.

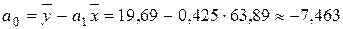Искомое уравнение регрессии имеет вид

.

Поскольку, проведенная в примере 9.1. проверка значимости парного коэффициента корреляции дала положительный результат, то это свидетельствует о значимости факторного параметра уравнения регрессии и адекватности этого уравнения в целом. Следовательно, это уравнение может быть использовано в практической деятельности без каких-либо ограничений – и для принятия управленческих решений (например, решения об увеличении объема реализованной продукции с целью увеличения балансовой прибыли), и для прогнозирования величины балансовой прибыли на основе предполагаемого объема реализованной продукции.

Оценим точность, с которой найденное уравнение описывает фактические значения результативного признака, рассчитав среднеквадратичную ошибку уравнения. Итерационную часть этого расчета представим в таблице 9.10.

Таблица 9.10

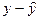
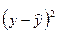
49,1	13,2	13,4045	-0,2045	0,041820
53,2	15,7	15,1470	0,5530	0,305809
54,8	15,3	15,8270	-0,5270	0,277729
60,3	19,0	18,1645	0,8355	0,698060
65,4	19,5	20,3320	-0,8320	0,692224
66,0	21,0	20,5870	0,4130	0,170569
69,7	21,4	22,1595	-0,7595	0,576840
72,4	23,7	23,3070	0,3930	0,154449
73,0	23,0	23,5620	-0,5620	0,315844
75,0	25,1	24,4120	0,6880	0,473344
Итого	196,9	-	-	3,706689

.

.

Таким образом, среднеквадратичная ошибка найденного уравнения регрессии составляет 2,7% от среднего значения результативного признака, что свидетельствует о высокой точности этого уравнения.

Проведем интерпретацию уравнения регрессии на основе среднего коэффициента эластичности:

.

Согласно значению среднего коэффициента эластичности при увеличении среднего значения объема реализованной продукции на один процент средний уровень балансовой прибыли в рамках наблюдаемой совокупности предприятий увеличится на 1,379 %.

Разница в процентах между изменением результата и изменением фактора обусловлена наличием в линейном уравнении парной регрессии параметра 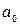. Если 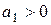, то при относительное изменение результата опережает относительное изменение фактора (как в нашем случае), а при – запаздывает. Если , то все наоборот.

Если интерпретируется линейное уравнение множественной регрессии, то разница в процентах между изменением результата и изменением 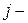го фактора объясняется наличием в частном уравнении регрессии параметра , который влияет на эту разницу так же, как параметр 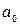в уравнении парной регрессии.

Пример 9.6. На основе результатов, полученных в примере 9.4, построим уравнение регрессии, описывающее линейную зависимость валового сбора зерновых культур от посевной площади и количества внесенных в почву удобрений, оценим границы его применения на практике и дадим интерпретацию его факторным параметрам.

Решение.

Имеет место двухфакторная линейная корреляция, поэтому для определения искомого уравнения регрессии необходимо решить систему уравнений

.

Учитывая результаты, полученные в таблице 9.9, система приобретает конкретный вид

.

Решая систему, получаем значения параметров уравнения регрессии , , . Тогда искомое уравнение регрессии имеет вид

.

Поскольку, проведенная в примере 9.4. проверка значимости множественного коэффициента корреляции дала положительный результат, то это свидетельствует об адекватности найденного уравнения регрессии в целом. Используя результаты, полученные в примере 9.4 (, , 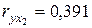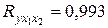), оценим значимость каждого из факторных параметров этого уравнения:

;

;

;

, .

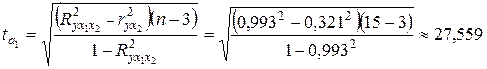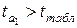Таким образом, найденное уравнение регрессии адекватно фактическим данным и, учитывая значимость всех параметров этого уравнения, может использоваться на практике без каких либо ограничений – как для принятия решения, так и для составления экономических прогнозов.

Для интерпретации уравнения рассчитаем средние коэффициенты эластичности:

;

.

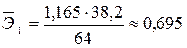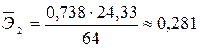Таким образом, при увеличении посевной площади на 1 % валовой сбор зерновых культур в среднем возрастает на 0,695 %. При увеличении количества внесенных в почву удобрений на 1 % валовой сбор зерновых культур в среднем возрастает на 0,281 %.

Если в качестве спецификации корреляционной модели выбрано нелинейное уравнение, являющееся внутренне линейным, то для определения его параметров также может быть использован метод наименьших квадратов, но с некоторыми допущениями.

Внутренне линейные уравнения принято разделять на нелинейные по факторам (например, полиномы произвольной степени и гиперболы) и нелинейные по параметрам (например, степенные и экспоненциальные).

Рассмотрим в качестве примера определение уравнения параболической регрессии

.

Данное уравнение является нелинейным по факторам, но линейным по параметрам, и легко линеаризуется.

Обозначим 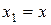, 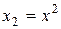. Тогда искомое уравнение принимает вид линейного уравнения

.

Согласно методу наименьших квадратов для определения параметров такого уравнения необходимо решить систему

Если от двухфакторной линейной регрессии вернуться к однофакторной параболической регрессии, то эта система примет вид

.

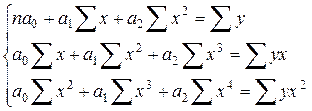Аналогично, при определении параметров гиперболы вида

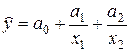
решают систему уравнений

.

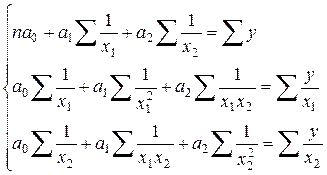Для оценки значимости параметров найденного уравнения и его адекватности фактическим данным используют те же методы, что и в случае линейной спецификации. При этом уравнение рассматривается в его вторичном линейном виде.

При линеаризации уравнений, нелинейных по параметрам, функциональному преобразованию в обязательном порядке подвергаются значения результативного признака. Поясним это на примере определения параметров двухфакторного экспоненциального уравнения

.

Прологарифмируем обе стороны уравнения:

.

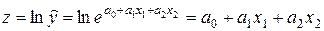Тогда применительно к новой форме регрессии метод наименьших квадратов заключается в решении задачи минимизации

.

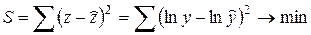В этом случае для определения параметров , 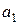и необходимо решить систему

.

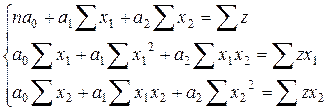В системе заменяют на и получают ее окончательный вариант

.

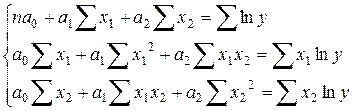При расчете параметров степенных уравнений функциональной замене подвергают как значения результата, так и значения факторов. Например, уравнение вида

линеаризуют посредством логарифмирования (основание логарифма не имеет значения). Вначале получают уравнение, нелинейное по факторам, но линейное по параметрам:

.

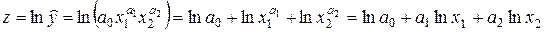Продолжая линеаризацию и применяя метод наименьших квадратов, получают окончательный вариант системы уравнений

.

Замена исходных значений результативного признака на функционально зависимые снижает точность в определении параметров уравнения регрессии. Их значения, рассчитанные методом наименьших квадратов, будут несколько смещены относительно искомых значений, потому что результаты решения задач

,

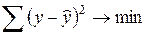для одних и тех же исходных данных в общем случае не совпадают. Учитывая содержание метода наименьших квадратов, решение первой задачи должно удовлетворять условию

,

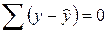а второй – условию

.

Вместе с тем, очевидно, что при нелинейном характере зависимости 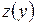всегда имеет место неравенство

.

Если пренебречь указанными обстоятельствами, то для определения искомого нелинейного уравнения, после его приведения к линейному виду, и оценки его точности и адекватности, можно использовать те же методы, что в отношении линейных уравнений.

Оценку эластичности нелинейной корреляции по факторам осуществляют на основе общей формулы коэффициента эластичности, предварительно рассчитав соответствующие частные производные корреляционной функции. Примечательно, что для степенных уравнений регрессии – парной или множественной, факторный коэффициент эластичности является постоянной величиной, равной соответствующему факторному параметру уравнения. Например, для уравнения вида :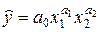

;

.

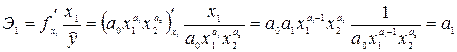Если нелинейное уравнение регрессии не может быть линеаризовано, то для определения его параметров вместо метода наименьших квадратов используют другие более сложные итерационные методы. Поскольку в большинстве случаев для исследования взаимосвязей между статистическими признаками, характеризующими социально-экономические явления и процессы, достаточно использовать линейные или внутренне линейные уравнения, то рассмотрение этих методов в рамках данного учебного пособия не имеет смысла.

Дата добавления: 2014-01-07