Матрицы и действия с ними

Системы линейных уравнений и их исследование.

Тема 1. Постановка задачи.

Повторение. Системы линейных уравнений с двумя неизвестными, методы их решения. Равносильные системы – системы с одним и тем же множеством решений. Равносильные преобразования: прибавление одного и того же числа к обеим частям уравнения, умножение обеих частей уравнения на одно и тоже число, замена одного из уравнений суммой этого уравнения и другого, умноженного на одно и тоже число.

Не только в математике, но и в жизни, люди нередко ставят и пытаются решать задачи, которые не имеют решения. Нам нужно научиться определять: имеет ли система одно решение, нуль решений или множество решений.

Определение 1.1. Системой линейных алгебраических уравнений (СЛАУ), содержащей m уравнений и n неизвестных, называется выражение следующего вида:

(1)

где 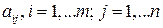- коэффициенты системы, 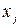- неизвестные, - свободные слагаемые. СЛАУ линейная потому что все не­известные в первой степени.

Определение 1.2. Совокупность чисел называется решением системы, если она обращает все уравнения в тождества.

Определение 1.3. Система (1) совместна, если она имеет хотя бы одно решение и несовместна, если она не имеет ни одного решения.

Определение 1.4. Система (1) называется однородной, если все свободные члены равны 0.

С понятием СЛАУ связано понятие матрицы.

Определение 1.5. Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =

Основные действия над матрицами

Матрица может состоять как из одной строки, так и из одного столбца и называется вектором.

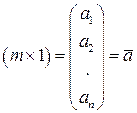или .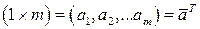

Вообще говоря, матрица может состоять даже из одного элемента. Нулевая матрица – это матрица, все элементы которой равны 0. Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Определение 1.6. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение 1.7. Матрица вида 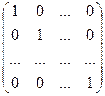= E, называется единичной матрицей.

Определение 1.8. Если a_mn = a_nm, то матрица называется симметрической.

Пример 1.1. 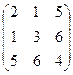- симметрическая матрица.

Определение 1.9. Квадратная матрица вида 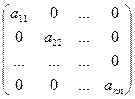называется диагональной матрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц.

Определение 1.10. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij ± b_ij

С = А + В = В + А.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

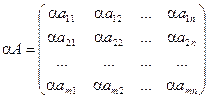
a (А+В) =aА ± aВ

А(a±b) = aА ± bА

Пример 1.2. Даны матрицы А = 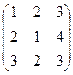; B = , найти 2А + В.

2А = , 2А + В = .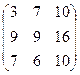

Определение 1.11. Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

.

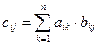Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц

1. Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O, где О – нулевая матрица.

2. Операция умножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

2. Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС,

(А + В)С = АС + ВС.

4. Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

5. Если определено произведение АВ, то определено произведение В^ТА^Т и выполняется равенство: (АВ)^Т = В^ТА^Т, где индексом Т обозначается транспонированная матрица.

Определение 1.12. Матрицу В называют транспонированнойматрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = 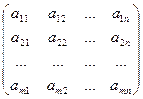; В = А^Т=;

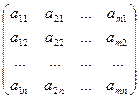другими словами, b_ji = a_ij.

В качестве следствия из предыдущего свойства 5 можно записать, что:

(ABC)^T = C^TB^TA^T,

при условии, что определено произведение матриц АВС.

Свойства транспонированной матрицы проверить самостоятельно.

- ;

- ;

- ;

- .

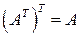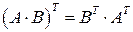6. Заметим также, что для любых квадратных матриц det(AB) = detA×detB.

Понятие det (определитель, детерминант) будет рассмотрено ниже.

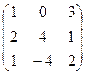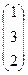Пример 1.3. Даны матрицы А = , В = , С = 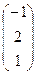и число a = 2. Найти А^ТВ+aС.

A^T = 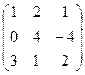; A^TB = 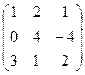×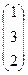= = 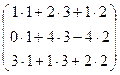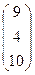; aC = 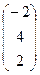; А^ТВ+aС = += .

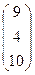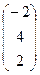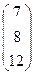Пример 1.4. Найти произведение матриц А = и В = .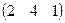

АВ = ×= .

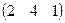ВА = 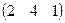×= 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

Пример 1.5. Найти произведение матриц А=, В =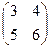

АВ = ×= = .

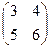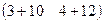В матричной форме СЛАУ выглядит следующим образом.

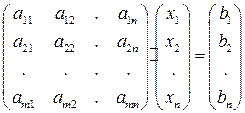(2)

Определение 1.13. Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов.

Для самостоятельного решения:

1. Вычислить .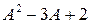

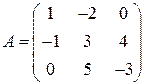
Дата добавления: 2014-01-07