Гипербола. В окружности (x – a)2 + (y – b)2 = R2 центр имеет координаты (a; b)

М

Эллипс

Окружность

В окружности (x – a)² + (y – b)² = R² центр имеет координаты (a; b).

Пример 2.1. Найти координаты центра и радиус окружности, если ее уравнение задано в виде 2x² + 2y² – 8x + 5y – 4 = 0.

Решение. Для нахождения координат центра и радиуса окружности выделим полные квадраты:

x² + y² – 4x + 2,5y – 2 = 0

x² – 4x + 4 –4 + y² + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2)² + (y + 5/4)² – 25/16 – 6 = 0

(x – 2)² + (y + 5/4)² = 121/16

Отсюда находим О(2; -5/4); R = 11/4.

Определение 2.1. Эллипсом называется кривая, заданная уравнением .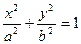

Определение 2.2. Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

у

F₁ O F₂ х

F₁, F₂ – фокусы. F₁(-c; 0); F₂(c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

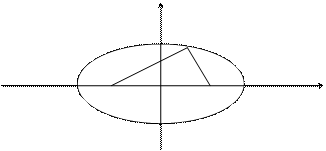
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением a² = b² + c².

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2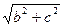(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r₁ + r₂ = a – c + a + c. Т.к. по определению сумма r₁ + r₂ – постоянная величина, то, приравнивая, получаем: a² = b² + c²

r₁ + r₂ = 2a.

Определение 2.3. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

е = с/a.

Т.к. с < a, то е < 1.

Определение 2.4. Величина k = b/a называется коэффициентом сжатияэллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса. Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e².

Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность. Если для точки М(х₁, у₁) выполняется условие: 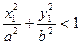, то она находится внутри эллипса, а если 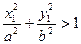, то точка находится вне эллипса.

Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения: r₁ = a – ex, r₂ = a + ex.

Доказательство. Выше было показано, что r₁ + r₂ = 2a. Кроме того, из геометрических соображений можно записать:

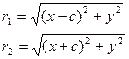
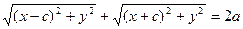
После возведения в квадрат и приведения подобных слагаемых:

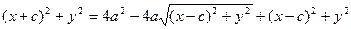
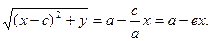
Аналогично доказывается, что r₂ = a + ex. Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения: x = a/e; x = -a/e.

Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример 2.2. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: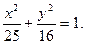

1) Координаты нижней вершины: x = 0; y² = 16; y = -4.

2) Координаты левого фокуса: c² = a² – b² = 25 – 16 = 9; c = 3; F₂(-3; 0).

3) Уравнение прямой, проходящей через две точки:

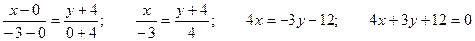
Пример 2.3. Составить уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), большая ось равна 2.

Решение. Уравнение эллипса имеет вид: 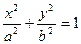. Расстояние между фокусами: 2c = 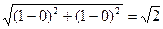, таким образом, a² – b² = c² = ½, по условию 2а = 2, следовательно а = 1, b = 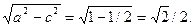Итого: .

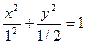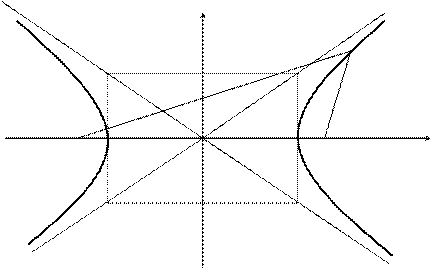
Определение 2.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

M(x, y)

b

a

r₁ r₂

F₁

По определению ïr₁ – r₂ï= 2a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

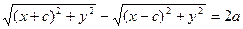
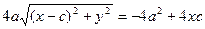
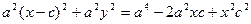
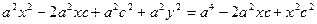
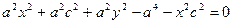
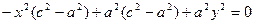
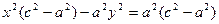
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось)

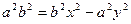
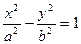. Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы. Ось 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

Определение 2.6. Отношение 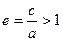называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось. С учетом того, что с² – а² = b²:

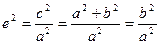
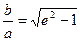
Если а = b, e = 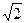, то гипербола называется равнобочной (равносторонней).

Определение 2.7. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .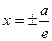

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

Пример 2.4. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса .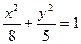

Для эллипса: c² = a² – b². Для гиперболы: c² = a² + b².

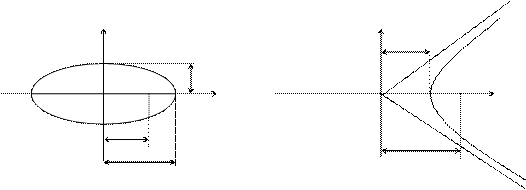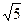
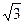
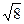
Уравнение гиперболы: .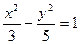

Пример 2.5. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением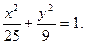

Находим фокусное расстояние c² = 25 – 9 = 16. Для гиперболы: c² = a² + b² = 16, e = c/a = 2; c = 2a; c² = 4a²; a² = 4;

b² = 16 – 4 = 12.

Итого: 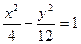- искомое уравнение гиперболы.

Дата добавления: 2014-01-07