Программирования (ЭММ ЛП)

ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЛИНЕЙНОГО

Экономико-математическая модель задачи линейного программирования (ЭММ ЛП) в общем случае имеет следующий вид.

Найти максимум или минимум линейной функции

f = е c_j x_j а max (min)

при условиях (ограничениях)

е a_ij x_j 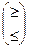b_i (i =1, 2,..., m);

x_j і 0 (j =1, 2,..., n),

где j	–	номер переменной;
n	–	число переменных;
i	–	номер ограничения;
m	–	число ограничений;
xj	–	переменные;
aij	–	технико-экономические коэффициенты;
cj	–	коэффициенты целевой функции;
bi	–	объемы ограничений.

Совокупность чисел x_j удовлетворяющих выше перечисленным условиям (ограничениям), называется допустимым решением (планом).

Допустимое решение, при котором целевая функция задачи принимает свое максимальное (минимальное) значение, называется оптимальным.

Множество решений задачи линейного программирования является выпуклым. Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую комбинацию (на плоскости – отрезок). Множество решений задачи ЭММ ЛП называется многогранником решений, а всякая угловая точка многогранника решений – вершиной. В случае, когда ЭММ ЛП оптимальна, т.е. целевая функция принимает максимальное (минимальное) значение более в одной вершине, то решением является выпуклая линейная комбинация этих вершин (на плоскости – отрезок).

Возникло линейное программирование в СССР. В 1939 г. появилась работа Л.В. Канторовича «Математические методы организации и планирования производства», где впервые был предложен метод решения экстремальных экономических задач, условия которых выражались уравнениями первой степени. В этом же году в СССР была сформулирована транспортная задача. За разработку методов линейного программирования академику Л.В. Канторовичу была присуждена Нобелевская премия (метод потенциалов).

В конце 40-х годов Д.Б. Данцинг разработал универсальный метод решения линейных оптимизационных задач – симплекс метод. В настоящее время симплекс метод имеет много разновидностей и почти все они запрограммированы для ПЭВМ.

Процесс решения ЭММ ЛП можно условно разбить на следующие этапы:

– постановка задачи (условие задачи и нормативно-справочная информация);

– формализация задачи (построение структурной ЭММ);

– построение развернутой схемы ЭММ;

– ввод данных в ПЭВМ и оптимизация ЭММ;

– анализ полученного решения и выводы.

При составлении постановки задачи особое внимание необходимо обратить на выбор критерия оптимизации ЭММ ЛП. Критерий оптимизации ЭММ ЛП – это показатель качества решения задачи. От правильного определения критерия оптимизации будет зависеть и наиболее эффективное распределение ресурсов.

Для наглядного представления основных элементов ЭММ ЛП и ее решения целесообразно использовать геометрическую интерпретацию или геометрический метод решения данных моделей.

В приведенных ниже задачах 1.1– 1.5 требуется:

– решить задачу ЛП с двумя переменными графическим методом;

– проверить решение задачи на ПЭВМ (программный комплекс «Блок-3»).

Основные теоремы раздела линейного программирования.

Теорема 1. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное (минимальное) значение более чем в угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинации этих точек.

Теорема 2 (об оптимальном решении в ограниченной области). Если область допустимых решений системы ограничена, то оптимальное решение существует и совпадает хотя бы с одним из опорных решений системы.

Теорема 3 (об оптимальном решении в ограниченной области). Если область допустимых решений не ограничена, то оптимальное решение, совпадающее по крайней мере с одним из опорных решений, существует только тогда, когда линейная функция ограничена сверху для задачи максимизации или снизу для задачи минимизации.

Теорема 4 (фундаментальная). Если задача линейного программирования имеет оптимальное решение (в ограниченной области всегда, а в неограниченной области в зависимости от ограниченности линейной функции), то оно совпадает, по крайней мере с одним из опорных решений системы ограничительных уравнений.

Теорема 5 (об альтернативном оптимуме). Если максимум или минимум линейной функции достигается в нескольких опорных решениях, то любое оптимальное решение есть выпуклая линейная комбинаия оптимальных решений.

Дата добавления: 2014-01-07