
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формы представления булевых функций
|
|
|
|
Дадим определения, необходимые для задания булевых функций.
Элементарная конъюнкция (дизъюнкция) – это логическое произведение (сумма) любого числа независимых логических переменных, входящих в нее с инверсией или без инверсии не более одного раза. Число входных переменных называется рангом элементарной конъюнкции (дизъюнкции).
Соседними называются элементарные конъюнкции (дизъюнкции) одного и того же ранга, содержащие одни и те же переменные, но отличающиеся знаком инверсии одной из переменных.
Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ), например:
(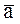 Ù b Ù
Ù b Ù ) Ú (
) Ú ( Ù c) Ú
Ù c) Ú  или
или 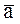 b
b  +
+  c +
c +  .
.
Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ), например:
(a Ú b Ú  )Ù (
)Ù ( Ú
Ú Ú d) Ù (
Ú d) Ù ( Ú
Ú ) или (a + b +
) или (a + b +  ) (
) (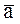 +
+ + d) (
+ d) ( +
+  ) (далее для упрощения восприятия булевых функций будем использовать второй вид записи).
) (далее для упрощения восприятия булевых функций будем использовать второй вид записи).
Теоремы разложения (см. п.п. 2.2) можно применить ко всем переменным, определяющим булеву функцию, тогда, например, используя первую теорему разложения для функции трех переменных f(a,b,c), получим:
f(a,b,c) = a·b·c·f(1,1,1) + 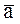 ·b·c· f (0,1,1) + a·
·b·c· f (0,1,1) + a· ·c·f(1,0,1) + a·b·
·c·f(1,0,1) + a·b· ·f(1,1,0) + +
·f(1,1,0) + +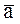 ·
· ·c·f(0,0,1) +
·c·f(0,0,1) + 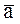 ·b·
·b· · f(0,1,0) + a·
· f(0,1,0) + a· ·
· · f(1,0,0) +
· f(1,0,0) + 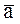 ·
· ·
· · f(0,0,0).
· f(0,0,0).
Каждая элементарная конъюнкция этого выражения составлена из набора всех переменных в прямом или инверсном виде и некоторого коэффициента, принимающего значение функции, если в ней положить равным единице прямое значение соответствующей переменной, а нулю – инверсное. Нетрудно заметить, что при этом по закону нулевого множества элементы с нулевым значением функции обратятся в ноль и останутся лишь наборы переменных при единичном значении функции, которые далее будем называть конституентами разложения единицы, или минтермами.
|
|
|
Если применить вторую теорему разложения, то получим форму разложения функции на конституенты нуля:
f(a,b,c) = [a+b+c+f(0,0,0) ] [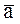 +b+c+f(1,0,0)] [a+
+b+c+f(1,0,0)] [a+ +c+f(0,1,0] [a+b+
+c+f(0,1,0] [a+b+ + +f(0,0,1)] Ù [
+ +f(0,0,1)] Ù [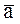 +
+ +c+f(1,1,0)] [
+c+f(1,1,0)] [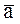 +b+
+b+ +f(1,0,1)] [a+
+f(1,0,1)] [a+ +
+ +f(0,1,1)] [
+f(0,1,1)] [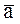 +
+ + +
+ + + f(1,1,1)].
+ f(1,1,1)].
Здесь, по закону универсального множества, каждая элементарная дизъюнкция с единичным значением функции принимает также единичное значение, и в результате остаются только те дизъюнкции переменных, инверсные значения которых определяют нулевое значение функции. Эти дизъюнкции называются конституентами разложения нуля, или макстермами. Такие методы разложения распространяются на функции с любым числом переменных.
Раскладывая булевы функции на конституенты, мы получаем т.н. совершенные формы. Совершенной дизъюнктивной формой (СДНФ) называется дизъюнкция конституентов единицы (минтермов), а совершенной конъюнктивной формой – конъюнкция конституентов нуля (макстермов).
Любую сколь угодно сложную булеву функцию можно преобразовать в ДНФ или КНФ, а затем в совершенные формы (СДНФ или СКНФ). Для этого необходимо прежде всего, используя теорему де Моргáнa, исключить инверсии над функциями, перейдя к формам, в которых имеются инверсии только над одиночными переменными. Затем с использованием законов булевой алгебры привести логические выражения к дизъюнктивной или конъюнктивной формам. Понятие совершенных форм используется при минимизации функций и для определения равносильности. Две булевы функции считаются равносильными, если их СДНФ и СКНФ полностью совпадают.
| Переменные | Функция | Десятичный эквивалент | |||
| a | b | c | d | Y | |
Таблица 2.1 Одной из самых распространенных форм представления булевых функций является таблица истинности (таблица состояний). Таблица истинности определяет значение функции для всех возможных состояний входных переменных. Поскольку любая логическая переменная может принимать только два значения – 0 и 1, то для булевой функции «n» входных переменных число значений будет определяться показательной функцией 2n.
|
|
|
Функция является полностью определённой, если для любого набора входных переменных известны её значения (0 или 1).
Булева функция является не полностью определённой (неполной), если есть один или несколько наборов переменных, при которых значение функции не определено (может быть и 0, и 1) или ее не существует. Такие значения функции называются фиктивными (Ф). Пример задания не полностью определенной функции представлен табл. 2.1.
Каждый набор логических переменных представлен двоичным числом n-го разряда, и ему, следовательно, соответствует определенное десятичное число. Десятичное число, соответствующее двоичному набору логических переменных, называется десятичным эквивалентом. Таким образом, булеву функцию можно представить с помощью десятичных эквивалентов:
Y1 = { 0,1,3,5,8}; Y0 = {2,7,9,13,15}.
Оставшиеся наборы, не заданные таблицей истинности, по всей вероятности, будут фиктивными YФ = {4,6,10,11,12,14}.
По таблице истинности можно получить совершенные формы записи булевых функций. Так, для записи в виде СДНФ нужно из таблицы выбрать единичные наборы переменных, представить их в виде конституентов единицы и произвести их дизъюнкцию.
СДНФ: Y =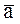


 +
+ 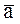

 d +
d +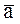
 c d +
c d +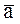 b
b d + d
d + d 

 .
.
Для записи в форме СКНФ нужно выбрать из таблицы нулевые наборы переменных, проинвертировать переменные в каждом из этих наборов, представить в виде конституентов нуля и произвести их конъюнкцию.
СКНФ: Y=(a+b+ +d)(a+
+d)(a+ +
+ +
+ )(
)(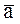 +b+c+
+b+c+ )(
)(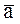 +
+ +c+
+c+ )(
)(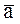 +
+ +
+ +
+ ).
).
Аналогично можно составить СДНФ и СКНФ по десятичным эквивалентам, определяющим булеву функцию.
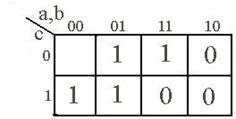
Матрица Карно представляет собой специально организованные таблицы соответствия, обладающие тем замечательным свойством, что любые две соседние клетки матрицы определяют «соседние» наборы переменных, т.е. наборы, отличающиеся значением только одной переменной. Клетки, расположенные по краям матрицы, также являются соседними и обладают этим свойством. Это достигается благодаря кодированию столбцов и строк матрицы специальным циклическим кодом Грея.
|
|
|
Еще одним свойством матриц Карно является то, что при увеличении количества переменных на единицу матрица увеличивается вдвое, поскольку число клеток матрицы определяется показательной функцией «2n».
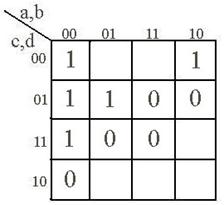
В клетках матрицы, как в таблице истинности, проставляются значения определяемой булевой функции – 0 или 1. Клетки, соответствующие фиктивным состояниям, обычно оставляют пустыми. Например, на рис. 2.1а представлена матрица Карно, определяющая функцию, заданную таблицей истинности (табл. 2.1). По сути дела, матрица Карно – это та же таблица состояний, но в более компактной форме.
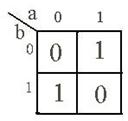
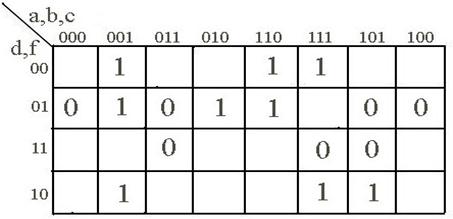
На рис. 2.1b, c, d показаны соответственно матрицы Карно для двух, трех и пяти переменных.
a b c
d
Рис. 2.1.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 903; Нарушение авторских прав?; Мы поможем в написании вашей работы!