Лекция 4. Наряду с задачей отыскания максимального потока большое практическое значение имеет задача экономичного распределения потока по дугам транспортной сети

Транспортная задача

Наряду с задачей отыскания максимального потока большое практическое значение имеет задача экономичного распределения потока по дугам транспортной сети, получившая название транспортной задачи. Поскольку транспортная сеть во многих случаях представляет собой схему организации перевозок каких-либо грузов, то решение транспортной задачи позволяет определить наиболее рациональный план перевозок, т.е. такое распределение маршрутов, которое обеспечивает, например, минимальную стоимость перевозок или доставку грузов к потребителю в кратчайшее время.

Первая задача получила название транспортной задачи по критерию стоимости, а вторая — по критерию времени.

Для каждой дуги (x_i, x_j) введём ещё один вес - стоимость прохождения единицы потока по ней - и обозначим его d_ij.

Транспортную задачу по критерию стоимости в терминах теории графов можно сформулировать следующим образом. Даны транспортная сеть с наибольшим потоком j^m и поток j_z, который должен быть пропущен по этой транспортной сети. Требуется найти такое распределение потока j_z по дугам, которое обеспечивает минимальную стоимость прохождения потока. При этом для каждой дуги должно выполняться соотношение
j(x_i, x_j)£ c_ij, а стоимость прохождения потока j(x_i, x_j) по дуге (x_i, x_j) равна d_ijj(x_i, x_j).

Для решения этой задачи будем рассматривать величины d_ij как длины соответствующих дуг. В этом случае стоимость прохождения потока j по какому-либо пути m от x₀ до z будет равна произведению длины этого пути на величину потока j и задача минимизации стоимости прохождения потока сведется к решению рассмотренной ранее задачи нахождения кратчайшего пути в графе от x₀ до z. При отсутствии ограничений на пропускную способность дуг, кратчайший путь является путем, который обеспечивает минимальную стоимость прохождения потока.

При наличии ограничений на пропускную способность дуг задача решается в несколько этапов, путем нахождения частичных потоков на каждом этапе. Общий путь решения задачи состоит в следующем.

В графе G ₁ = (X, R), изображающем транспортную сеть с длинами дуг d_ij = l(x_i, x_j) l, ищется кратчайший путь m₁ от x₀ до z. Пусть c₁ — пропускная способность этого пути. По нему пропускается поток

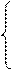j_z, если j_z£с_1;

j₁=

с₁, если j_z>c₁.

Если j_z £ c₁, то задача решена и путь m₁ является наиболее экономичным для потока j_z.

Если j_z > c₁, то поток j₁ рассматриваем как частичный и переходим к графу G₂, который получается из графа G₁ путем замены пропускных способностей дуг c_ij на c’_ij из соотношения

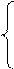c_ij - c₁ для uÎ m₁;

c`_ij =

с₁ для u Ï m₁.

При этом дуги, у которых c’_ij = 0, исключаются из рассмотрения. Поток, распределение которого ищется в графе G₂, принимаем равным j`₁=j_z-j_1.

Теперь возникает первоначальная задача отыскания наиболее экономичного распределения потока j’_z, но уже по отношению к графу G₂. Ее решение дает путь m₂ с пропускной способностью c₂, через который пропускается частичный поток

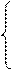j`<sub>z</sub>, если j`_z£с₂;

j₂=

с₂, если j`_z>c₂.

Если j’_z £ c₂, то задача решена и наиболее экономичным распределением потоков в графе G₁ будет прохождение потока j₁ по пути m₁ и потока j₂ по пути m₂.

Если j’_z > c₂, то следует перейти к новому графу G₃ и найти новый частичный поток j₃ . Этот процесс повторяется до тех пор, пока сумма частичных потоков не достигнет значения j_z. Эти частичные потоки, пропущенные по графу G₁, и дают оптимальное распределение потока j_z.

Для иллюстрации описанного метода рассмотрим наиболее часто встречающийся вариант транспортной задачи по критерию стоимости.

Однородный груз имеется на станциях х₁,...,x_т в количествах a₁,...,a_m. Его требуется доставить на станции y₁,..., у_r в количествах b₁,..., b_r. Предполагается, что общее количество требуемого груза равно имеющимся запасам: S a_i =S b_j.

Стоимость перевозки груза со станции x_i на станцию у_i равна d_ij. Требуется найти наиболее экономичные маршруты перевозки грузов. Исходные данные удобно записывать в виде табл. 2.4.

Таблица 2.4

	b1	…	br
A1	d11	…	d1r
…	…	…	…
am	dm1	…	dmr

Транспортная сеть для этой задачи строится следующим образом. Вход x₀ соединяется с каждой из вершин x_i дугой с пропускной способностью с(x₀, x_i) = a_i. Каждая из вершин y_i соединяется с выходом z дугой с пропускной способностью с(y_i, z) = b_j. Стоимость прохождения потока по дугам (x₀, x_i) и (y_i, z) считается равной нулю. Наконец, каждая вершина x_i соединяется с каждой вершиной y_i дугой с бесконечной пропускной способностью, стоимость прохождения единицы потока по которой равна d_ij. Далее к этой транспортной сети применяется рассмотренный метод.

Пример. Найти наиболее экономичные маршруты для транспортной задачи, заданной табл. 2.5

Таблица 2.5

Применяя описанный выше метод к транспортной сети, построенной по табл. 2.5 (рис. 2.12), находим частичные потоки и маршруты, перечисленные в табл. 2.6 в порядке их получения.

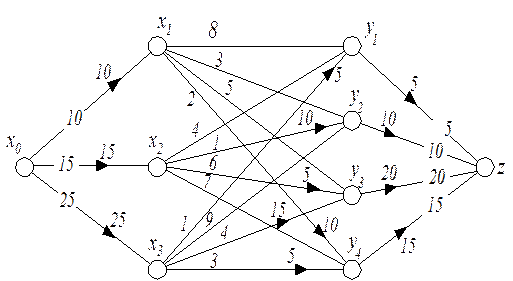
Рис. 2.12

Таблица 2.6
Номер маршрута	Маршрут (хi, yj)	Частичный поток jk, ед.	dij	Стоимость перевозки dij jk, ед.
	(х3, y1)
	(х2, y2)
	(х1, y4)
	(х3, y4)
	(х3, y3)
	(х2, y3)
Всего	–		–

Следовательно, разобранный метод решения транспортной задачи дает, по существу, способ нахождения величин частичных потоков j(x_i, y_j), минимизирующих указанную сумму.

Решение транспортной задачи по критерию времени рассмотрим на примере транспортной сети, заданной табл. 2.6, в которой величины d_ij будем теперь трактовать как время, необходимое на перевозку груза из пункта x_i в пункт y_j и обозначить далее через t_j. С подобными задачами можно столкнуться три транспортировке скоропортящихся продуктов, при доставке средств помощи в районы стихийных бедствий, при вывозе зерна нового урожая в заготовительные пункты и т. п. Во всех этих задачах стоит требование доставки всех грузов в пункты назначения за возможно более короткий промежуток времени.

Рассмотрим общий путь решения этой задачи. Предположим, что каким-либо методом найдено некоторое распределение потока j_z в графе G, изображающем рассматриваемую транспортную сеть. Выделим из
графа G частичный граф G', в который включим только дуги, участвующие в передаче потока j_z. Пусть m — некоторый путь, ведущий из x₀ в z, a t_m — время прохождения потока по этому пути. Очевидно, что время, необходимое на перевозку всех грузов из x₀ в z, будет определяться путем, имеющим наибольшую продолжительность прохождения потока, так как перевозка грузов по остальным путям закончится раньше. Следовательно, время Т, требуемое на перевозку всех грузов, будет
равно T =max t_m.

Решение транспортной задачи по критерию времени сводится, таким образом, к тому, чтобы выделить из графа G такой частичный граф G’, который был бы способен пропустить весь поток j_z и в котором длительность наиболее продолжительного пути была бы минимальной по сравнению со всеми другими подобными графами.

Задача решается последовательным улучшением графа G' путем удаления из него наиболее продолжительных путей и введения более коротких, но не примененных ранее, и соответствующего перераспределения потока j_z.

Обратимся к рассматриваемому примеру. В качестве первого приближения к наилучшему решению примем решение, полученное на основе критерия стоимости. Распределение потоков для этого случая показано на рис.2.12. Из этого рисунка видим, что время прохождения потока по наиболее продолжительному маршруту (х₂, y_з) равно 6. Однако оказались неиспользованными менее продолжительные маршруты (х₁, y₂), (х₂, y₁), (х₁, y_з). Возможно, что использование какого-либо из этих маршрутов позволит исключить маршрут (х₂, y_з).

Построим частичный граф G', в который включим только дуги графа G, имеющие t_ij < 6 и в котором распределение потока останется тем же, что и в графе G. Граф G' показан на рис. 2.13, где для удобства вершины y_j обозначены через x_m+j = x_3+j. Поток j’_z через этот граф равен 45 ед., т. е. меньше, чем первоначальный поток j_z = 50 ед. Этот поток является полным, так как в графе G' все пути из х₀ в z содержат насыщенные дуги. Однако возможно, что он не является наибольшим.

Если наибольший поток в графе G' равен j_z, то найдется распределение этого потока, при котором наиболее продолжительный путь будет иметь время t_m < 6 ед. Следовательно, дальнейшее решение задачи сводится к определению наибольшего потока в графе G'.

На рис. 2.13 произведена разметка вершин графа G' в соответствии с алгоритмом Форда и Фалкерсона. Разметка вершин указывает на существование пути (х₀, х₂, х_4, х₃, х₆, z), на котором поток в направлении от х₀ к z может быть увеличен на 5 ед.

Рис. 2.13.

Этот добавочный поток показан стрелками. Как видим, наибольший поток в графе G' равен j_z = 50 ед. и наиболее продолжительный маршрут имеет время 4 ед. Дальнейшего уменьшения времени прохождения потока добиться невозможно, так как к вершине y_з(х₆) не идут маршруты со временем, меньшим 4 ед.

Окончательное распределение частичных потоков по маршрутам, дающее решение транспортной задачи по критерию времени, приведено в табл. 2.7.

Таблица 2.7
Маршрут, ед.	Частичный поток	Время прохождения потока
(х2, y2)
(х1, y4)
(х3, y4)
(х2, y1)
(х3, y3)
–	jz = 50	Tmax = 4

СПИСОК ЛИТЕРАТУРЫ

1. Новиков Ф. А. Дискретная математика для программистов: Для студентов вузов / Ф.А. Новиков. - СПб.; М.; Харьков; Минск: Питер, 2001. - 304 с.

2. Яблонский, Сергей Всеволодович. Введение в дискретную математику: Учеб. пособие для студентов вузов, обучающихся по спец. "Прикладная математика" / С. В. Яблонский. - 3-е изд., стер. - М.: Высшая математика, 2001. - 384 с.

Дата добавления: 2014-01-07