
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы де Моргана
|
|
|
|
Возьмем правую часть равенства. Согласно закону ассоциативности
раскроем скобки и получим:
(АÈС)Ç(ВÈС)=АÇВÈСÇВÈАÇСÈСÇС=АÇВÈС (упростили используя
закон поглощения). Из записи закона ассоциативности и закона
дистрибутивности видно, что один закон можно получить из другого,
заменив знаки “È” и “Ç”, следовательно, законы двойственны.
4. Закон поглощения
Если А содержится в В, то АÈB=В.
Согласно аксиоме объединения в результирующее множество входят элементы, принадлежащие хотябы одному А или В, а так как все А входят в В то справедливо:
АÈB=В
АÈАÇМ=А
Исходя из определения операции пересечения ясно, что АÇМ содержится в А.В итоге получаем А.
Следствие:
Если М=1, то АÈА=А
5. Свойство степени.
Если множество пересекается с самим собой, то из определения пересечения следует
АÇА=А
Эти законы позволяют выразить законы объединения и пересечения друг через друга с использованием операции дополнения:
 а) АÈВ=
а) АÈВ=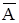 Ç
Ç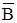

Доказательство:
Обозначим через М: М=АÈВ и 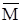 =
=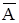 Ç
Ç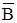 . Если теперь объединение М и
. Если теперь объединение М и 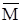 даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È 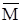 = А È В È
= А È В È 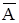 Ç
Ç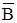 = АÈ(В È
= АÈ(В È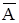 )Ç(В È
)Ç(В È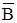 ). Используя определение дополнения получим:
). Используя определение дополнения получим:
М È 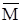 = АÈВÈ
= АÈВÈ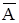 =1ÈВ=1=I
=1ÈВ=1=I
 б) АÇВ=
б) АÇВ=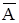 È
È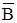

Доказательство:
Обозначим через М: М=АÇВ и 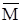 =
=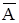 È
È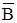 . Если теперь объединение М и
. Если теперь объединение М и 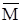 даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È 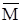 = А Ç В È
= А Ç В È 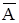 Ç
Ç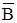 =(
=(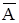 È А) Ç (В È
È А) Ç (В È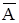 )È
)È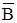 = ВÈ
= ВÈ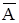 È
È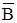 =1È
=1È 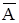 =1=I
=1=I
Законы де Моргана так же являются двойственными.
АÇВ=АВ.
ВЫВОДЫ ПО РАЗДЕЛУ.
1. АÌА
2. Если АÌВ и ВÌА, то А=В
3. Если АÌВ и ВÌС, то АÌС
4. Æ Ì A
|
|
|
5. А Ì I
6. А È В =В È А
7. А Ç В =В Ç А
8. АÈ(ВÈС)=(АÈВ)ÈС
9. АÇ(ВÇС)=(АÇВ)ÇС
10. А È А = А
11. А Ç(ВÈС)=(АÇВ)È(АÇС)
12. А È (ВÇС)=(АÈВ) Ç (АÈС)
13. А È Æ = А
14. А È I= I
15. А Ç I = A
16. А Ç A = A
17. А Ç Æ = Æ
18. Если АÌВ, то АÈВ=В, АÇВ=А
19. А È 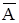 = I
= I
20. A Ç 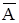 = Æ
= Æ
21. 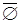 =I
=I
22. 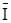 =Æ
=Æ
23. 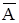 = A
= A
24. Если АÌВ, то 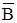 Ì
Ì 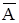
25. (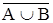 ) =
) = 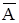 Ç
Ç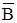
26. (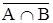 ) =
) = 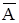 È
È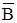
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1497; Нарушение авторских прав?; Мы поможем в написании вашей работы!