
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замечательные пределы
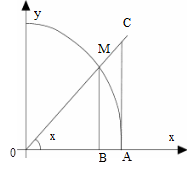
|
Рассмотрим функцию
 =
=  . Она не определена в точке
. Она не определена в точке  = 0, тем не менее предел её в этой точке существует и равен единице. Докажем это. Из чертежа при
= 0, тем не менее предел её в этой точке существует и равен единице. Докажем это. Из чертежа при
0 <  <
< 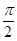 ясно, что
ясно, что
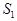 <
< 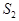 <
< 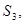 (1)
(1)
где 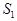 и
и 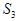 – площади треугольников ОМВ и ОСА, а
– площади треугольников ОМВ и ОСА, а 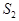 – площадь кругового сектора. Радиус окружности будем считать равным единице. Тогда, выражая площади через угол
– площадь кругового сектора. Радиус окружности будем считать равным единице. Тогда, выражая площади через угол  , неравенство (1) перепишем так:
, неравенство (1) перепишем так: 
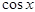 ×
×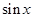 <
< 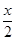 <
< 
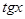 , или
, или
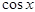 <
< 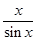 <
< 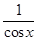 Þ
Þ 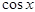 <
<  <
< 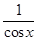 . (2)
. (2)
В неравенстве (2) все функции являются четными, поэтому оно верно и для отрицательных  , т.е. при
, т.е. при 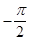 <
<  <
< 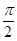 ,
,  ¹ 0. Устремляя
¹ 0. Устремляя  к нулю и пользуясь теоремой о двух милиционерах, получим
к нулю и пользуясь теоремой о двух милиционерах, получим
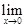
 = 1. (3)
= 1. (3)
Формулу (3) называют первым замечательным пределом.
Прежде, чем перейти ко второму замечательному пределу, приведем формулу бинома Ньютона
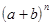 =
= 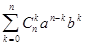 , (4)
, (4)
где 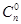 = 1,
= 1, 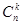 =
= 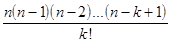 ,
, 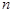 Î N,
Î N,
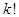 = 1×2×3×...×
= 1×2×3×...×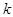 .
.
Формулу (4) можно доказать методом математической индукции. Мы её докажем позже другим методом.
Рассмотрим последовательность 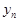 =
= 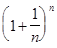 . Используя формулу бинома Ньютона, получим
. Используя формулу бинома Ньютона, получим
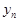 = 1 +
= 1 + 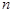 ×
×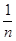 +
+ 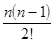
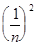 +
+ 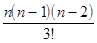
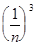 +... +
+... +
+ 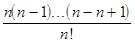
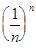 = 1 + 1 +
= 1 + 1 + 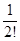
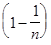 +
+
+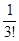
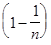
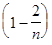 +...+
+...+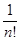
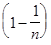
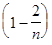 ...
...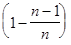 . (5)
. (5)
Из (5) видно, что последовательность {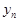 } монотонно возрастающая, т.к. при замене n на n + 1 каждое слагаемое в (5) возрастает и добавляется еще одно положительное слагаемое.
} монотонно возрастающая, т.к. при замене n на n + 1 каждое слагаемое в (5) возрастает и добавляется еще одно положительное слагаемое.
Покажем теперь, что эта последовательность ограниченна сверху. Действительно,
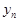 < 1 + 1 +
< 1 + 1 + 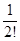 +
+ 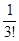 +... +
+... + 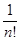 £ 1 + 1 +
£ 1 + 1 + +
+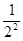 +...+
+...+ 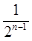 =
=
= 1 + 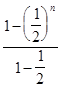 = 1 + 2 –
= 1 + 2 – 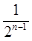 £ 3, " n Î N. (6)
£ 3, " n Î N. (6)
(Сначала мы отбросили скобки меньшие единицы, и результат возрос. Затем учли, что 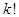 ³
³ 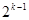 и воспользовались формулой суммы членов убывающей геометрической прогрессии со знаменателем q =
и воспользовались формулой суммы членов убывающей геометрической прогрессии со знаменателем q =  ).
).
Итак, последовательность {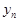 } монотонно возрастает и ограниченна сверху, следовательно, имеет предел (см. Теорему 2 §2). Этот предел называют числом е.
} монотонно возрастает и ограниченна сверху, следовательно, имеет предел (см. Теорему 2 §2). Этот предел называют числом е.
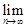
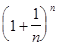 = е. (7)
= е. (7)
Число е является иррациональным, е = 2,718....
Рассмотрим теперь функцию  =
= 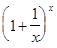 и докажем, что она имеет предел при
и докажем, что она имеет предел при 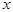 ® + ¥ равный е. Для любого положительного действительного числа
® + ¥ равный е. Для любого положительного действительного числа 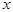 имеет место неравенство n £
имеет место неравенство n £ 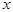 < n + 1. Для обратных величин этого неравенства получим
< n + 1. Для обратных величин этого неравенства получим
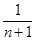 <
< 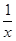 £
£ 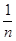 Þ 1 +
Þ 1 + 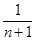 < 1 +
< 1 + 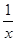 £ 1 +
£ 1 + 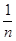 .
.
Если левую часть последнего неравенства возвести в степень n, среднюю – в степень x, а правую – в степень n + 1, то неравенство только усилится, т.е.
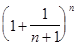 <
< 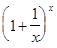 £
£ 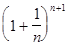 . (8)
. (8)
Легко убедиться, что 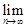
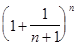 = e,
= e, 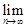
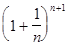 = e.
= e.
Поэтому из (8) по теореме о двух милиционерах следует, что
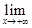
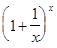 = e. (9)
= e. (9)
Покажем теперь, что 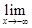
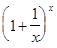 = e. Действительно,
= e. Действительно,
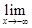
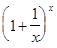 =
= 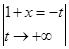 =
= 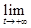
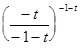 =
=
= 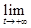
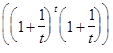 = e.
= e.
Последняя формула и формула (9) называются вторым замечательным пределом.
Можно доказать, что
1) 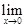
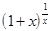 = e, 4)
= e, 4) 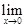
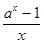 =
= 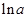 ,
,
2) 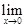
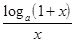 =
= 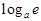 , 5)
, 5) 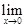
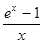 = 1,
= 1,
3) 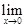
 = 1, 6)
= 1, 6) 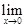
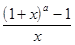 =
= 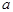 .
.
§ 7. Непрерывность функции. Классификация точек разрыва
Пусть функция 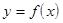 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Определение 1. Функция 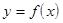 называется непрерывной в точке
называется непрерывной в точке  , если предел её в этой точке равен значению функции в этой точке, т.е. если
, если предел её в этой точке равен значению функции в этой точке, т.е. если
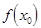 =
= 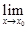
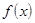 . (1)
. (1)
Пример 1. Покажем, что функция  =
= 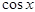 непрерывна в точке
непрерывна в точке  = 0. Действительно,
= 0. Действительно, 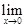
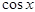 = 1 (см.пр.2 §3) и
= 1 (см.пр.2 §3) и 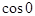 = 1, т.е. предел функции равен её значению. Согласно определению функция
= 1, т.е. предел функции равен её значению. Согласно определению функция  =
= 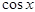 непрерывна в точке
непрерывна в точке
 = 0.
= 0.
Следствие 1. Если функция 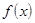 непрерывна в точке
непрерывна в точке  , то к пределу можно перейти под знаком функции, т.е.
, то к пределу можно перейти под знаком функции, т.е.
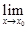
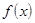 =
= 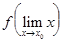 . (2)
. (2)
Действительно, поскольку  =
=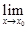
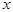 , то
, то 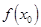 =
=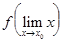 =
=
= 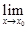
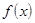 , т.к. функция непрерывна. Следствие доказано.
, т.к. функция непрерывна. Следствие доказано.
Разность 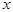 –
–  =
= 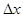 называют приращением аргумента, а разность
называют приращением аргумента, а разность 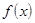 –
– 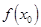 =
= 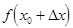 –
– 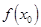 =
= 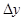 – приращением функции в точке
– приращением функции в точке 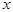 =
=  .
.
Следствие 2. Если функция непрерывна, то бесконечно малому приращению аргумента 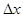 соответствует бесконечно малое приращение
соответствует бесконечно малое приращение 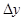 , т.е.
, т.е.
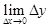 = 0. (3)
= 0. (3)
Действительно, перепишем равенство (1) так:
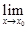
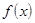 –
–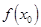 =0,
=0, 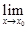 (
(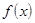 –
–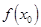 ) =
) =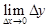 = 0. (4)
= 0. (4)
Следствие доказано.
Следствие 3. Если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.
Чтобы доказать это следствие, достаточно равенство (4) прочитать справа налево.
Если требования непрерывности функции в точке  не выполняются, т.е. функция не определена в точке
не выполняются, т.е. функция не определена в точке  или предел функции в точке
или предел функции в точке  не существует, или существует, но не равен значению функции в этой точке, то функция называется разрывной в точке
не существует, или существует, но не равен значению функции в этой точке, то функция называется разрывной в точке  , а сама точка
, а сама точка  называется точкой разрыва функции.
называется точкой разрыва функции.
Определение 2. Если функция непрерывна в каждой точке интервала (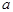 ,
,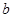 ), то она называется непрерывной на этом интервале. Если
), то она называется непрерывной на этом интервале. Если 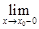
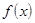 =
= 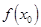 , то функция называется непрерывной в точке
, то функция называется непрерывной в точке  слева. Аналогично при
слева. Аналогично при 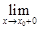
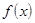 =
=
= 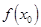 – непрерывной в точке
– непрерывной в точке  справа.
справа.
Определение 3. Если функция непрерывна в каждой точке интервала (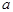 ,
,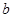 ),
), 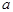 <
< 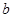 и в точке
и в точке 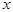 =
= 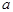 она непрерывна справа, а в точке
она непрерывна справа, а в точке 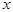 =
= 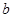 – слева, то она называется непрерывной на отрезке [
– слева, то она называется непрерывной на отрезке [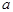 ,
,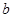 ].
].
Пример 2. Доказать, что функция  =
= 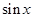 непрерывна в каждой точке своей области определения.
непрерывна в каждой точке своей области определения.
Доказательство. Пусть 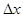 – приращение аргумента в произвольной точке
– приращение аргумента в произвольной точке  области определения функции. Тогда
области определения функции. Тогда
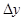 = sin (
= sin ( +
+ 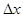 ) – sin
) – sin = 2sin
= 2sin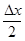 ×cos (
×cos ( +
+ 
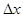 ).
).
Поскольку sin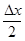 ® 0 при
® 0 при 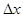 ® 0 (см. упражнение. в §3 гл.2), то и
® 0 (см. упражнение. в §3 гл.2), то и 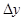 ® 0 при
® 0 при 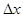 ® 0 (см. теорему 2 §4 гл.2). Тогда согласно следствию 3 функция
® 0 (см. теорему 2 §4 гл.2). Тогда согласно следствию 3 функция  =
= 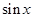 непрерывна в точке
непрерывна в точке  .
.
Что и требовалось доказать.
Аналогично можно доказать, что все основные элементарные функции непрерывны в своих областях определения. При этом, под основными элементарными функциями понимают следующие пять функций:
1) степенную  =
= 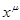 ,
, 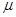 Î R;
Î R;
2) показательную  =
= 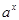 ,
, 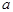 > 0,
> 0, 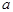 ¹ 1;
¹ 1;
3) логарифмическую  =
= 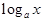 ,
, 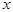 > 0,
> 0, 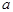 > 0,
> 0, 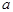 ¹ 1;
¹ 1;
4) тригонометрические  = sin
= sin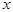 ,
,  = cos
= cos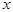 ;
;
5) обратные тригонометрические  = arcsin
= arcsin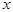 ,
, 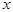 Î [ –1, 1],
Î [ –1, 1], 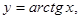
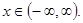
Пример 3. Исследовать на непрерывность функцию
 =
=  в точке
в точке  = 0.
= 0.
Решение. Поскольку точка  = 0 не входит в область определения этой функции, то она терпит разрыв в этой точке, не смотря на то, что имеет предел в этой точке.
= 0 не входит в область определения этой функции, то она терпит разрыв в этой точке, не смотря на то, что имеет предел в этой точке.
Пример 4. Исследовать на непрерывность функцию
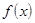 = sgn
= sgn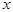 в точке
в точке  = 0.
= 0.
Решение. 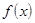 =sgn
=sgn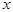 =
=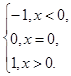 Очевидно,
Очевидно, 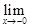
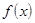 = –1,
= –1, 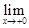
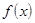 = +1, а
= +1, а 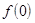 = 0. Поэтому эта функция разрывна в точке
= 0. Поэтому эта функция разрывна в точке  = 0.
= 0.
Пример 5. Исследовать на непрерывность функцию
 = sin
= sin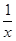 в точке
в точке  = 0.
= 0.
Решение. Т.к. функция не определена в точке  = 0 то она терпит в ней разрыв. Отметим, что эта функция не имеет предела в точке
= 0 то она терпит в ней разрыв. Отметим, что эта функция не имеет предела в точке  = 0 (см. пр.1 §3 гл.2).
= 0 (см. пр.1 §3 гл.2).
Пример 6. Исследовать на непрерывность функцию  =
= 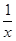 в точке
в точке  = 0.
= 0.
Решение. Поскольку функция не определена в точке
 = 0, то она разрывна в точке. Заметим, что
= 0, то она разрывна в точке. Заметим, что 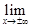
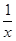 = ±¥.
= ±¥.
Пример 7. Исследовать на непрерывность функцию Дирихле
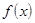 =
= 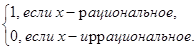
Решение. Функция определена в каждой точке числовой оси. Пусть  – произвольная точка числовой оси. Выберем две последовательности аргумента
– произвольная точка числовой оси. Выберем две последовательности аргумента  и
и 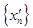 , сходящиеся к
, сходящиеся к  . Пусть члены первой последовательности рациональные числа, а второй иррациональные. Тогда соответствующие последовательности значений функции
. Пусть члены первой последовательности рациональные числа, а второй иррациональные. Тогда соответствующие последовательности значений функции 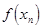 =1 и
=1 и 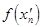 = 0 сходятся к единице и к нулю соответственно. А это означает, что данная функция не имеет предела. Данная функция разрывная в каждой точке числовой оси.
= 0 сходятся к единице и к нулю соответственно. А это означает, что данная функция не имеет предела. Данная функция разрывная в каждой точке числовой оси.
Определение 4. Если функция имеет предел в точке  , но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
, но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называется устранимым.
Если функция имеет в точке  односторонние пределы, не равные между собой, то
односторонние пределы, не равные между собой, то  называется точкой разрыва первого рода. При этом
называется точкой разрыва первого рода. При этом 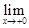
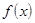 –
– 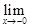
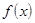 =
= 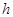 называется скачком функции в точке
называется скачком функции в точке  .
.
Если хотя бы один из односторонних пределов не существует или бесконечный в точке  , то эта точка разрыва второго рода.
, то эта точка разрыва второго рода.
Например, точка  в примере 3 является точкой устранимого разрыва, а в примере 4 – разрывом первого рода. Разрыв в примерах 5,6,7 второго рода.
в примере 3 является точкой устранимого разрыва, а в примере 4 – разрывом первого рода. Разрыв в примерах 5,6,7 второго рода.
Определение 5. Функция непрерывная на отрезке [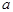 ,
,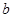 ] за исключением конечного числа точек этого отрезка, в которых она терпит разрывы первого рода, называется кусочно-непрерывной на этом отрезке. Функция называется кусочно-непрерывной на всей числовой оси, если она кусочно-непрерывна на любом отрезке этой оси.
] за исключением конечного числа точек этого отрезка, в которых она терпит разрывы первого рода, называется кусочно-непрерывной на этом отрезке. Функция называется кусочно-непрерывной на всей числовой оси, если она кусочно-непрерывна на любом отрезке этой оси.
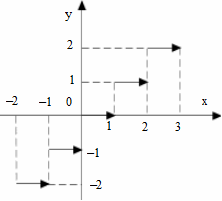
Пример 8. Исследовать на непрерывность функцию
 =
= 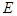 (
(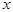 ), целую часть величины
), целую часть величины 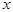 .
.
|
Решение. Очевидно, функция терпит разрывы при 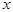 Î Z. В остальных точках она непрерывная. При этом
Î Z. В остальных точках она непрерывная. При этом 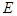 (0) = 0,
(0) = 0,
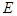 (± n) = ± n, n Î N,
(± n) = ± n, n Î N,
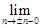
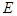 (
(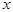 ) = ± n – 1 ¹
) = ± n – 1 ¹
¹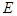 (± n),
(± n),
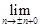
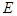 (
(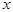 ) = ± n =
) = ± n =
=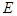 (± n).
(± n).
Таким образом, функция имеет точки разрыва только первого рода, в них она непрерывна справа. Это пример кусочно-непрерывной функции на всей числовой оси.
|
Дата добавления: 2014-01-07; Просмотров: 781; Нарушение авторских прав?; Мы поможем в написании вашей работы!