Характер и скорость сходимости ряда Фурье

Как отмечалось выше, тригонометрический ряд Фурье любой кусочно-непрерывной функции сходится в среднем квадратичном. Однако, ряд Фурье может сходиться и равномерно, все зависит от свойств разлагаемой функции. Если числовой ряд 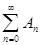коэффициентов ряда Фурье (16) §3 сходится, то сам ряд Фурье (16) сходится равномерно на всей числовой оси, т.к. ряд 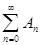является для него мажорантным.

Заметим, что ряд Фурье можно почленно интегрировать.

Теорема 1. Если функция 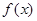кусочно-непрерывная на отрезке и в каждой точке 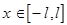имеет конечные односторонние производные 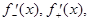то ряд Фурье этой функции сходится в каждой точке этого отрезка, а его сумма (без доказательства).

Например, функции и 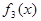примера §3 отвечают условиям теоремы 1, поэтому ряды Фурье для этих функций сходятся в каждой точке отрезка а в точке 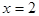т.е. равны полусумме своих пределов слева и справа, согласно теореме 1.

Теорема 2. Пусть функция и все ее производные до порядка непрерывны на отрезке и удовлетворяют условию

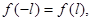
Если кроме того функция 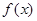имеет на отрезке кусочно-непрерывную производную порядка 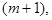то ряд Фурье этой функции сходится равномерно и его можно 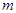раз почленно дифференцировать. Полученный ряд будет сходиться равномерно на (без доказательства).

Следствие. В условиях теоремы 2 остаток ряда Фурье имеет следующий порядок:

(1)

Например, функция 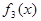примера §3 удовлетворяет условиям теоремы 2 при Ряд Фурье для этой функции сходится равномерно, но почленно дифференцировать его нельзя.

При практическом использовании рядов Фурье важен не только характер сходимости (средняя, поточечная, равномерная), но и скорость сходимости к нулю коэффициентов Фурье. Из оценок остатка (1) видно, что скорость сходимости зависит от свойств разлагаемой в ряд Фурье функции, а именно, чем глаже функция, т.е. чем больше она имеет производных, тем быстрее сходится ее ряд Фурье.

Например, ряд Фурье функции 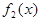в §3 сходится быстрее, чем ряды Фурье функций и т.к. она непрерывная на всей оси, а функции и 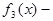разрывные.

Дата добавления: 2014-01-07