Задачи математической физики. Метод Даламбера

Для уравнений мат. физики решаются как задача Коши, так и граничные задачи. Различают три вида граничных задач: первого, второго и третьего рода. Пусть решение уравнения (1) §3 ищется внутри или вне некоторой области D c границей 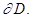Если на границе задано условие

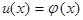
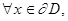(1)

то это граничная задача первого рода, или задача Дирихле. Если на границе задано условие

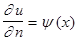
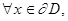(2)

где 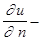производная функции по направлению нормали к границе области D, то это вторая граничная задача, или задача Неймана. В третьей, или смешанной задаче, граничные условия записываются в виде:

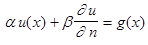
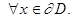(3)

Для уравнений Лапласа и Пуассона возможны только граничные задачи. Для уравнений теплопроводности и волнового уравнения решается и задача Коши.

Из основных методов решения уравнений математической физики отметим следующие: метод характеристик, метод интегральных преобразований и метод Фурье (разделение переменных).

Не рассматривая сам метод характеристик, воспользуемся его результатом - решением уравнения колебания струны

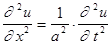(4)

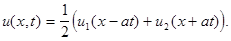(5)

Непосредственной подстановкой (5) в (4) убедимся, что (5) является решением уравнения (4), если произвольные функции 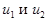дважды дифференцируемы. Решение называют прямой бегущей волной, а решение 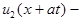обратной бегущей волной. Таким образом, общее решение (5) представляет собой суперпозицию (наложение) прямой и обратной волн.

Струну будем считать бесконечной и решим задачу Коши с начальными условиями 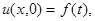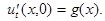(6)

Требуя выполнения начальных условий (6), из (5) получим

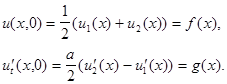
(7)

Интегрируя последнее уравнение из (7), получим

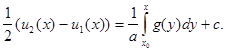(8)

Из (7) и (8) найдем неизвестные функции 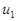и

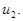
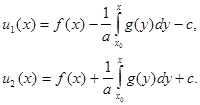(9)

Подставляя (9) в (5), получим решение задачи Коши

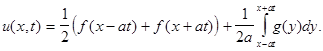(10)

Формула (10) называется решением Даламбера задачи Коши для уравнения колебания струны.

Дата добавления: 2014-01-07